2.8. Рівномірний розподіл
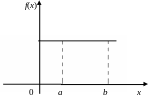
Неперервна випадкова величина має рівномірний розподіл на інтервалі (а, b), якщо всі її можливі значення неперервно заповнюють цей інтервал і рівноймовірні на ньому, тобто
Рівномірний розподіл називають також законом рівномірної щільності. При визначенні рівномірного розподілу можна говорити про рівномірний розподіл випадкової величини Х на інтервалі або відрізку, оскільки ймовірність попадання в точку дорівнює нулю.
Виходячи з умови нормування щільності розподілу, знайдемо значення С:
Отже
Функція розподілу
F(x)
=
якщо
x
a
F(x)
=
якщо
x
(a,
b]
F(x)
=
якщо
x
>b.
Таким чином,
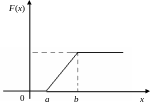
P(
<
x
<
)
=
F()
– F()
=
.
Математичне
сподівання M[x]
=
.
Дисперсія
D[x]
=
Середньо
квадратичне відхилення [x]
=
З графіка щільності ймовірності рівномірно розподіленої випадкової величини Х випливає, що моди немає, а медіана
Me
=
Ексцес неперервно розподіленої випадкової величини Х має таке значення:
