2.4.3. Основні властивості числових характеристик

1. Математичне сподівання центрованої випадкової величини:

Отже математичне сподівання центрованої випадкової величини дорівнює нулеві. Доведення для неперервної випадкової величини аналогічне.

2. Дисперсія випадкових величин

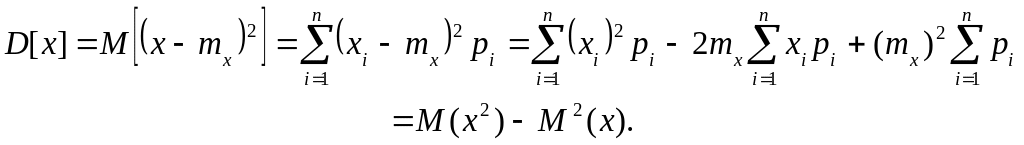
Тобто

Дисперсія випадкової величини дорівнює другому початковому моменту без квадрата математичного сподівання.

3. Аналогічно можна довести, що третій центральний момент

₃ = ₂– 3₂m_x + 2(m_x)².

4. Математичне сподівання константи

M[C] = C1 = C.

Математичне сподівання константи дорівнює самій константі.

5. Математичне сподівання суми випадкової і невипадкової величини дорівнює сумі математичних сподівань цих величин.

6. Константу можна виносити за знак математичного сподівання.

7. Дисперсія сталої величини дорівнює нулю.

8. Дисперсія центрованої і нецентрованої випадкової величини дорівнюють одна одній.

9. Постійний множник виноситься у квадраті за знак дисперсії.

2.5. Закони розподілу випадкових величин

2.5.1. Нормальний закон розподілу ймовірності неперервної випадкової величини

Нормальний розподіл в теорії ймовірності займає особливе місце, є найбільш розповсюдженим. Нормальному закону підкоряються ті величини, значення яких визначаються багатьма незалежними причинами, причому кожна з них впливає на випадкову величину незначно. Наприклад, випадкова величина – похибка виміру – може бути представлена як сума великої кількості порівняно малих доданків – елементарних похибок, кожна з яких викликана дією окремих причин, що залежить від інших. Яким би законам розподілу не була підлегла окрема елементарна похибка, особливості їх у сумі великого числа доданків, і сума опиняється підкореною до закону, близького до нормального.

Н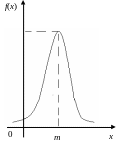 ормальний закон розподілу характеризуються щільністю ймовірності виду:

Крива розподілу по нормальному закону (крива Гауса) має холмоподібний вигляд, симетрична відносно прямої х = m.

Щільність розподілу (х)  0 при х  .Ми бачимо, що нормальний розподіл визначається двома параметрами : m і .

З’ясуємо їх зміст, для чого знайдемо основні числові характеристики випадкової величини Х – математичне сподівання і дисперсію.

а) за означенням математичне сподівання неперервної випадкової величини

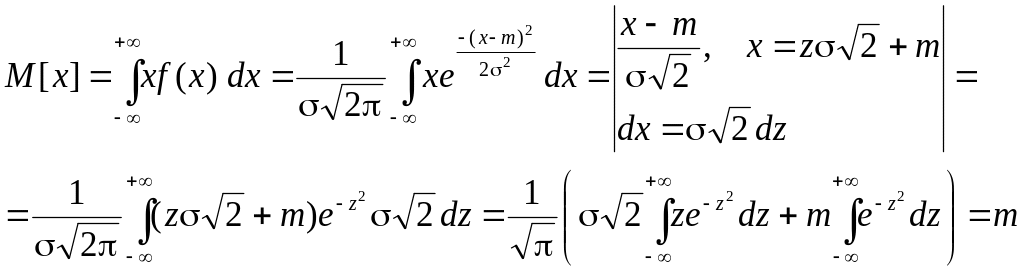
( – інтеграл Ейлера-Пуассона).

Таким чином, M[x] = m, тобто параметр дорівнює математичному сподіванню.

б) за визначенням дисперсії неперервної випадкової величини і враховуючи, що M[x] = m_x = m, маємо

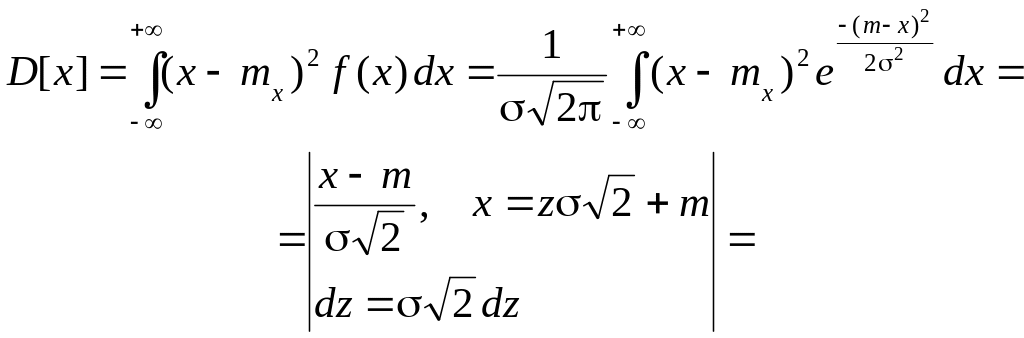
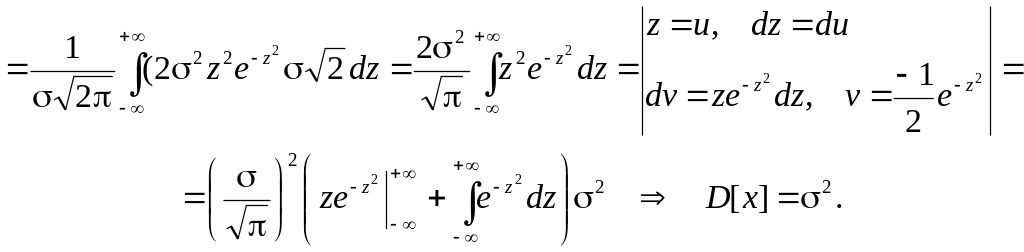
Тобто параметр  дорівнює середньому квадратичному відхиленню.

З’ясуємо, як впливають параметри m і  на форму кривої Гауса.

В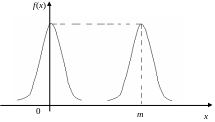 ідомо, що графік функції (х – m) одержується з графіка функції (х) шляхом зсуву останнього на величину х = m при  = соnst; графік (х) зміщується вздовж вісі ОХ, не змінюючи своєї форми f(x)

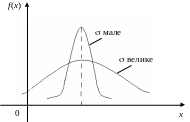
Із зростанням  максимальна ордината нормальної кривої спадає, а сама крива стає більш пологою, тобто стискується до вісі ОХ; при спаданні  нормальна крива стає більш “гостровершинною” і розтягується у додатному напрямі вісі ОY.

Якщо у формулі щільності ймовірностей покласти  = 1 і m = 0, то дістанемо нормовану щільність закону розподілу:

Інтеграл 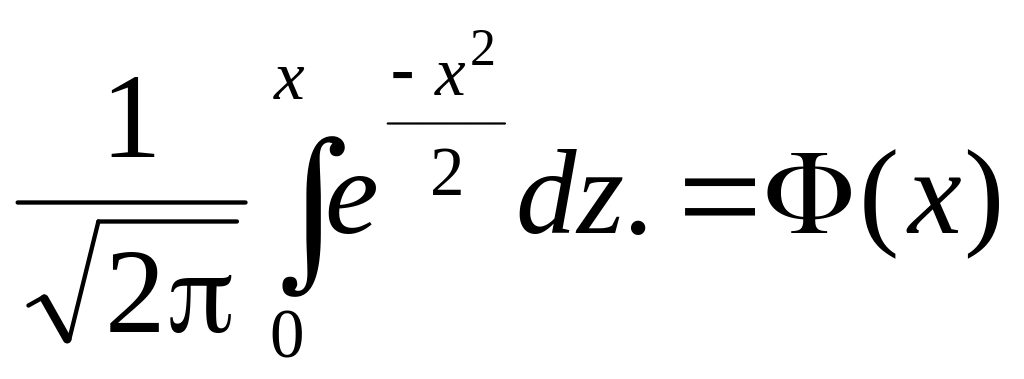=(х) називають інтегралом ймовірностей або функцією Лапласа. Він не береться в елементарних функціях і для нього існують спеціальні таблиці. (–х) = –(х); при х  5 (х) = 1/2. E_x = 0; k₃ = 0.