2.2. Функція розподілу

Всі можливі значення неперервної випадкової величини на відміну від дискретної не можна перерахувати, отже, неможливо задати закон розподілу для неперервної випадкової величини за допомогою ряду розподілу або многокутника розподілу.

Універсальною порівняно з рядом розподілу і многокутником розподілу є функція розподілу. Для функції розподілу використовуємо не ймовірність події Х = х, а ймовірність події Х < х.

Означення. Функцією розподілу (інтегральною функцією) F(х) називається ймовірність події, яка полягає в тому, що випадкова величина Х набуває значення меньше деякої змінної х: F(x) = P(X < x).

F(x) годиться як для дискретних, так і для неперервних випадкових величин.

Сформулюємо деякі загальні властивості функції розподілу (без доведення).

1. 0  F(x)  1 – ця властивість випливає із означення функції розподілу як ймовірності.

2. F(x) – неспадаюча функція свого аргументу, тобто при х₂ > х₁ F(x₂)  F(x₁) : F(х₁) = Р(Х < x₁), F(x₂) = P(X < x₂).

Рівність можлива тоді, коли немає шансів попасти в інтервал (х₁, х₂).

3. F(–) = 0.

4. F(+) = 1.

Ці рівності легко пояснити виходячи із геометричного змісту функції розподілу – ймовірність того, що випадкова величина набуває значень, розташованих зліва від точки х.

Якщо будемо необмежено переміщувати точку х вліво по осі абсцис, то попадання випадкової величини Х лівіше х у границі стає неможливою подією; природньо покласти, що ймовірність цієї події прямує до нуля, тобто F(–) = 0. Аналогічним чином необмежено переміщуючи точку х вправо, переконаємось, що F(+) = 1.

Графік функції F(х) є графік неспадаючої функції:

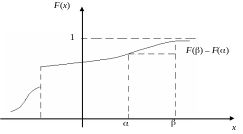
Знайдемо ймовірність того, що випадкова величина Х попадає на ділянку від  до .Умовимося лівий кінець ділянки включати, а правий не включати, тобто   Х < .Виразимо ймовірність цієї події через функцію розподілу величини Х.Для цього розглянемо три події: подія А полягає в тому, що Х < , подія В – Х < , подія С –   Х < .

Враховуючи, що А = В + С, згідно з теоремою додавання ймовірностей несумісних подій маємо:

Р(Х < ) = P(X < ) + P(  X < ) або F()=F()+P(X<) 

P( X < ) = F() – F(), (1)

тобто ймовірність попадання випадкової величини на заданий проміжок дорівнює приросту функції розподілу на цьому проміжку.

Чим більше крутість ділянки, тим більша ймовірність попасти на проміжок (, ).

Нехай функція розподілу F(x) неперервна. Знайдемо

Р(x  X < x + x) = F(x + x) – F(x) = F(x).

Знайдемо границю ймовірності при х  0 :

P(x  X < x + x)= F(x) (2)

Оскільки функція розподілу неперервна, нескінченно малому приросту аргументу відповідає нескінченно малий приріст функції. Звідси випливає, що F(x) = 0.

Звідси: для неперервної випадкової величини ймовірність набування конкретного значення внаслідок досліду практично дорівнює нулю. Тоді

P( X < ) = P(X = ) + P( < X < ) =F() – F() (3)

Здобутий результат можна порівняти з масою точки. Густина речовини відмінна від нуля, а маса точки цієї речовини практично дорівнює нулю.