Частина 2. Випадкові величини

2.1. Види випадкових величин. Ряд розподілу. Многокутник розподілу

Подальшим узагальненням і розширенням поняття випадкової події є випадкова величина.

Означення. Випадковою називається величина, яка у результаті випробування може прийняти те, чи інше значення, заздалегідь невідоме.

Випадкову подію можна розглядати як випадкову величину, що приймає тільки два значення – одиницю, коли подія відбулася (вірогідна) і нулю, коли – не відбулася (неможлива).

Усі результати, одержані раніше для випадкових подій, можна використати для випадкових величин. На практиці зустрічаються із двома видами випадкових величин: дискретними і неперервними.

Випадкова величина називається дискретною, якщо вона набуває окремих значень, які можна перерахувати (перенумерувати).

Приклади.

а) при киданні грального кубика число очок, що з’являється (1, 2, ..., 6);

б) число кораблів, що обробляються у порту за певний час;

в) число хлопчиків, що народжуються на кожну сотню пологів.

Неперервною випадковою величиною називається величина, можливі значення якої неперервно заповнюють деякий проміжок, і їх не можна перерахувати.

Приклади.

а) амплітуда морської хвилі у даній точці у даний момент часу;

б) швидкість повітря;

в) час очікування телефонного дзвінка.

У подальшому будемо випадкові величини позначати великими літерами X, Y, Z, ..., а їх можливі значення – маленькими літерами x, y, z, ... .

Для завдання дискретної випадкової величини треба перерахувати всі числові значення, які вона може прийняти і вказати їх ймовірності.

Задамо дискретну випадкову величину Х таблицею:

х	х1	х2	...	хn
р	р1	р2	...	рn

Одержана таблиця називається рядом розподілу дискретної випадкової величини Х.

Д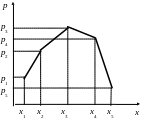 ля того, щоб надати ряду розподілу більш наочний вигляд, застосовують його графічне зображення: по осі абсцис відкладають всі можливі значення випадкових величин, а по осі ординат – ймовірності цих значень. Фігура, утворена послідовним з’єднанням здобутих точок відрізками прямих, називається многокутником розподілу. І ряд розподілу, і многокутник розподілу повністю характеризують закон розподілу дискретної випадкової величини.

Оскільки х₁, х₂, ..., х_n – всі можливі значення Х і утворюють повну групу несумісних подій, то

Введемо позначення: Р(Х = х_і) = р_і – ймовірність того, що випадкова величина Х приймає значення х_і, дорівнює р_і.

Приклад. Відбувається пальба по мішені. Ймовірність кожного влучення – р. Пальба відбувається до першого попадання. Випадкова величина Х – число зроблених пострілів. Побудувати ряд розподілу.

Розв’язання: можливі значення величини Х: 1, 2, 3,...Для того, щоб величина Х прийняла значення 1, необхідно, щоб подія А (влучення у ціль) відбулося при першому пострілі і його ймовірність р. Для того, щоб величина Х прийняла значення 2, необхідно, щоб при першому пострілі подія А не відбулася, а при другому – відбулася; ймовірність цього дорівнює pq (q = 1 – p).

Ряд розподілу:

Х	1	2	3	...	n
p	p	pq	pq²	...	pqⁿ‾¹

Для контролю підрахуємо суму ймовірностей: