1.4.5.Формула повної ймовірності

Ця формула є наслідком теорем додавання та добутку.

Нехай подія А може відбутися при умові появи однієї з несумісних подій H₁, H₂, ...,H_n, що утворюють повну групу. Останні події називають гіпотезами.

Відомі ймовірності гіпотез і умовні ймовірності P(A/H_і).Треба знайти Р(А) (рис. 2).

Маємо:

(1)



. (2)

Формула (2) одержується з (1) із наступних міркувань: оскільки події несумісні, то події H_іA також несумісні, а далі послідовно застосовуємо теореми про суму несумісних подій і про теорему про добуток подій.

Формула (2) називається формулою повної ймовірності.

1.4.6.Формула Байеса

Ця формула є наслідком теореми добутку і формули повної ймовірності.

Ставиться задача: маємо повну групу несумісних подій H₁, H₂, ..., H_n (гіпотези). Ймовірності гіпотез до досліду відомі і рівні P(H_і). Відомо, що у результаті досліду подія А відбулася. У зв’язку з появою події А гіпотези одержують нові ймовірності P(H_і /A). Їх треба знати. З теореми добутку маємо

P(AH_і) = P(A)P(H_і/A), або P(AH_і) = P(H_і)P(A/H_і), звідси маємо, що

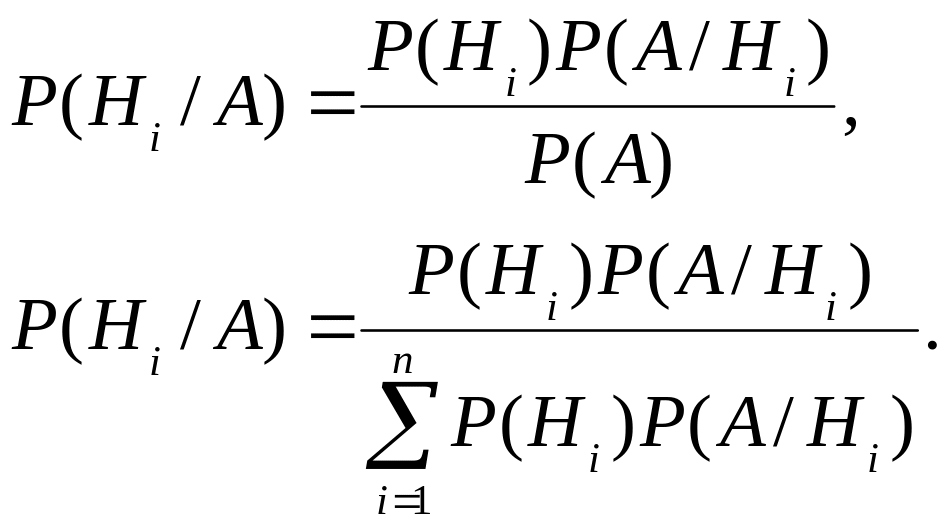(3)

(3) і є формулою Байеса (формула перерахунку ймовірностей).

Приклад. До магазину надходить товар з трьох баз. З першої надходить 20 %, з другої – 50 % і з третьої – 30 %.

Перша база постачає 70% товару першого ґатунку, друга – 80%, і третя – 40%.Куплений відвідувачем товар – першого ґатунку. Знайти ймовірність того, що цей товар надійшов з другої бази.

Розв’язання:

Згідно з формулою Байеса

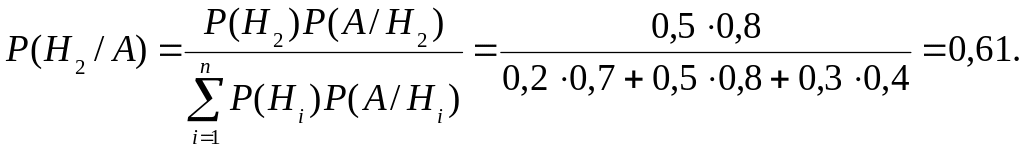
1.5. Повторення незалежних випробувань

1.5.1. Формула Бернуллі

В теорії масового обслуговування, теорії інформатиці зустрічаються задачі, в яких один і той же дослід повторюється неодноразово, а в результаті досліду подія А може статися, а може ні. У кожному досліді нас буде цікавити два наслідки :

настане подія А чи ні (настане ).

Нехай подія А настає у кожному випробуванні з однаковою ймовірністю, а ця ймовірність не залежить від того, чи відомі наслідки попереднього досліду. Такі випробування називаються незалежними від події А.

Прикладом незалежних подій може бути перевірка кількох партій виробів на брак, якщо процент браку у кожній з партій однаковий, а з кожної партії перевіряють один виріб.

Ставиться задача : нехай виконується n незалежних дослідів. Ймовірність появи події А у кожному з них однакова і дорівнює р. Знайти ймовірність того, що подія А з’явиться m разів в n дослідах. Нехай подія – поява події А в і-ому досліді, а – не поява в і-ому досліді. Подія В_m – подія А з’явилась рівно m разів.

До кожного доданку подія А входить m разів, – (n – m) разів. Якщо ймовірність події А дорівнює р, то .

Використовуючи теореми ймовірності суми несумісних подій та ймовірності добутку незалежних подій, дістанемо ймовірність події B_m. При цьому враховуємо, що число вище згаданних комбінацій дорівнює . Тому

Останню формулу ще записують

(1)

і називають формулою Бернуллі.

Приклад. Ймовірність влучення при одному пострілі дорівнює 0,8. Знайти ймовірність 5 влучень при 6 пострілах.

Розв’язання: р = 0,8; q = 0,2; n = 6; m = 5.