1.4.4. Теорема добутку ймовірностей

Введемо поняття незалежних і залежних подій. Подія А називається незалежною від події В, якщо ймовірність події А не залежить від того, відбулася подія В чи ні.

Подія А називається залежною від події В, якщо ймовірність події А залежить від того, відбулася подія В чи ні.

Ймовірність події В, яку обчислюють при умові, що подія А відбулася, називають умовною і позначають Р(В/А).

Приклад 1. Кидають дві монети. Подія А – поява цифри на першій, В – поява цифри на другій. У даному випадку ймовірність події А не залежить від В. А і В – незалежні події.

Приклад 2. В урні 7 білих і три чорних кульки. Двоє виймають із урни по одній кульці. Розглянемо події:

А – поява білої кульки у першої особи;

В – поява білої кульки у другої особи.

Ймовірність події А до того, як стало що-небудь відомо про подію В, тобто Р(А)=7/10. Якщо стало відомо, що подія В відбулася, то Р(А/В)=6/9, з чого робимо висновки, що подія А залежить події В.

Як бачимо, умову незалежності події а від події в можна записати у вигляді :

Р(А) = Р(А/В),

а умову залежності – у вигляді :

Р(А)  Р(А/В).

Теорема добутку ймовірностей.

Ймовірність добутку двох подій дорівнює добутку ймовірності однієї з них на умовну ймовірність іншої, обчислену при умові, що перше мало місце: Р(АВ)=Р(А)Р(В/А).

Доведення:

Доведемо теорему для схеми випадків. Нехай маємо n випадків, несумісних між собою, рівноможливих і таких, що утворюють повну групу подій. Зобразимо їх у вигляді n точок.

Вважаємо, що події А сприяє m випадків, а В – k. Оскільки ми не вважаємо, що А і В несумісні, то існує l випадків, що сприяють А і В разом. Тоді

Р(АВ)=l/n, P(A)=m/n, P(B/A)=l/m,

що і треба було довести.

Зауваження. При доведенні теореми не має значення, яку подію вважати першою, а яку другою. Тому ще і

Р(АВ)=Р(B)Р(А/В)

Наслідок 1.Якщо подія А не залежить від події В, то подія В не залежить від події А.

Доведення:

Із того, що А не залежить від В, випливає, що Р(А) = Р(A/В). Відомо, що Р(АВ) = Р(А)Р(В/А) або Р(АВ) = Р(В)Р(А/В). Звідси Р(А)Р(В/А)=Р(В)Р(А/В)  Р(В)=Р(В/А).

Останнє означає, що В не залежить від А.Отже, події А і В взаємонезалежні.

Таким чином події називаються незалежними, якщо поява однієї із них не змінює ймовірності появи іншої.

Наслідок 2. Ймовірність добутку двох незалежних подій дорівнює добутку ймовірностей цих подій.

Доведення:

Р(АВ)=Р(А)Р(В/А), але Р(В/А)=Р(В), бо події А і В незалежні за умовою. Отже, Р(АВ) = Р(А)Р(В).

Теорема добутку ймовірностей може бути узагальнена на випадок більш ніж двох подій.

Наприклад, Р(АВС) = Р(АВ)Р(С/АВ) = Р(А)Р(В/А)Р(С/АВ). Якщо події А, В, С незалежні, то Р(АВС) = Р(А)Р(В)Р(С).

Приклад. В партії з 10 виробів 6 виробів першого ґатунку, а 4 – другого. Знайти ймовірність того, що три перші закуплені вироби є вироби першого ґатунку.

Розв’язання:

Нехай подія А – всі три вироби першого ґатунку, – і-ий виріб першого ґатунку. Тоді А = А₁А₂А₃ Р(А) = Р(А₁)Р(А₂/А₁)Р(А₃/А₁А₂) = (6/10)(5/9)(4/8) = 1/6.

В заключенні відмітемо, що якщо події А і В сумісні, то теорема додавання має вигляд

Р(А + В) = Р(А) + Р(В) – Р(АВ)

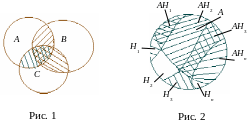
Справедливість теореми випливає з малюнка.

Р(А + В + С) = Р(А) + Р(В) + Р(С) – Р(АВ) – Р(АС) – Р(ВС) + Р(АВС).

Складаємо площі трьох кіл, а потім віднімаємо їх попарно спільні частини, але тоді ділянка, загальна для усіх трьох кіл залишається неврахованою. Для того, щоб не порушувати рівності, в правій частині слід додати ймовірність, що відповідає цій ділянці (pиc. 1).