
- •Питання 3 Транспонована матриця
- •Ранг матриці та способи його обчислення
- •Властивості рангу матриці
- •Необхідність[ред. • ред. Код]
- •Достатність[ред. • ред. Код]
- •Алгоритм[ред. • ред. Код]
- •Початок алгоритму.
- •Опис методу[ред. • ред. Код]
- •Визначення
- •Лінійна залежність і незалежність векторів. Розклад вектора за базисом
- •15.Пряма і площина в просторі. Взаємне розташування площин. Пряма як лінія перетину двох площин.
- •17.Основні числові множини: n, z, q, r, Числова пряма.
- •19.Числові послідовності та їх властивості: обмеженість, монотонність.
- •20.Означення границі послідовності. Геометрична інтерпретація. Способи задання послідовності . Приклади.
- •21.Єдиність границі числової послідовності. Обмеженість числової
- •2.5. Основні теореми про границю
- •Зауваження
- •Теорема 2.15.
- •Теорема 2.18. .
- •Название и зарубежная терминология[править | править исходный текст]
21.Єдиність границі числової послідовності. Обмеженість числової
послідовності. Монотонної послідовності.
Питання 22
Послідовність { }називається нескінченно малою, якщо для будь-якого додатнього числа ε, можна вказати таке натуральне число N, що при n≥N, всі елементи { } задовольняють нерівність | |<ε
Основні властивості нескінченно малих послідовностей[ред. • ред. код]
Сума двох нескінченно малих послідовностей є нескінченно мала послідовність.
Різниця двох нескінченно малих послідовностей є нескінченно мала послідовність.
Добуток двох нескінченно малих послідовностей є нескінченно мала послідовність.
Добуток нескінченно малої послідовності на дійсне число є нескінченно мала послідовність.
Якщо всі елементи нескінченно малої послідовності рівні певному числу c, то це число рівне нулю. ( c=0 )
Якщо елементи { } нескінченно великої послідовності відмінні від нуля, то послідовність {
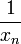 }
є нескінченно малою.
}
є нескінченно малою.2.5. Основні теореми про границю
Теорема 2.11. Границя сталого дорівнює сталому, тобто
 ,
де
,
де  .
.Доведення. Нехай
 ,
де
.
Розглянемо різницю
,
де
.
Розглянемо різницю  ,
маємо:
,
маємо:  –
нескінченно мала величина. За теоремою
2.4 маємо, що
–
нескінченно мала величина. За теоремою
2.4 маємо, що  .
.Теорема 2.12. Границя суми дорівнює сумі границь.
Доведення. Нехай, наприклад,
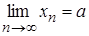 ,
, 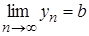 .
Покажемо, що
.
Покажемо, що  .
Дійсно
.
Дійсно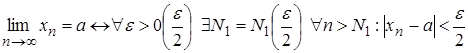 ;
;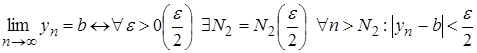 .
.За
 оберемо
оберемо 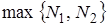 та
оцінимо модуль
та
оцінимо модуль 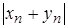 ,
маємо:
,
маємо: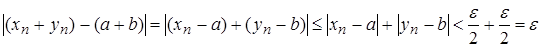 .
.Таким чином,
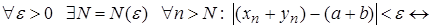
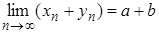 .
.Зауваження. Випадок суми довільного скінченного числа числових послідовностей доводиться аналогічно.
Теорема 2.13. Границя добутку дорівнює добутку границь.
Доведення. Нехай, наприклад, , . Покажемо, що
 .
Дійсно, якщо
,
то за теоремою 2.3
.
Дійсно, якщо
,
то за теоремою 2.3  ,
де
,
де 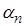 –
нескінченно мала величина. Аналогічно,
–
нескінченно мала величина. Аналогічно, 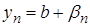 ,
де
,
де 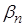 –
нескінченно мала. Тоді
–
нескінченно мала. Тоді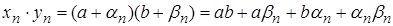 .
.Оскільки константа є величиною обмеженою, то за теоремою 2.6 величини
 є
нескінченно малими; за теоремою 2.5
величина
є
нескінченно малими; за теоремою 2.5
величина 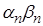 також
є нескінченно малою. Оскільки сума
трьох нескінченно малих величин є
нескінченно малою, то
також
є нескінченно малою. Оскільки сума
трьох нескінченно малих величин є
нескінченно малою, то  є
нескінченно мала і за теоремою 2.4.
є
нескінченно мала і за теоремою 2.4.Зауваження
1) Сталий множник можна виносити за знак границі.
Дійсно,
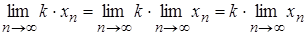 .
.2)

 .
.Дійсно,
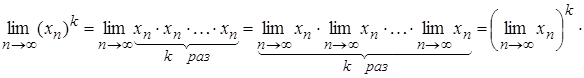
3)
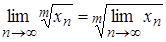 .
.Теорема 2.14. Границя частки двох послідовностей дорівнює частці границь цих послідовностей, якщо границя знаменника не дорівнює нулю, тобто
 ,
де
,
де 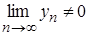 .
.Зауваження. Доведення даної теореми проводиться аналогічно доведенню теореми 2.13.
Теорема 2.15.
1)
 ,
де
,
де 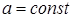 ;
;2)
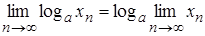 ,
де
.
,
де
.Теорема 2.16. Якщо для послідовності
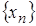 відомо,
що для всіх
відомо,
що для всіх 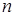
 і
,
то
і
,
то 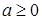 .
.Доведення. Проведемо доведення методом від супротивного. Нехай
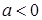 ,
але тоді
,
але тоді 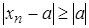 і
і 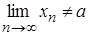 .
Остання рівність суперечить умові
теореми. Це означає, що наше припущення
хибне і
.
.
Остання рівність суперечить умові
теореми. Це означає, що наше припущення
хибне і
.Теорема 2.17. Якщо для послідовностей та
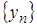 відомо,
що
відомо,
що 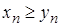 ,
то
,
то  .
.Доведення. За умовою теореми
 ,
тоді за теоремою 2.16
,
тоді за теоремою 2.16 .
.Теорема 2.18. .
Запам’ятай добре! Аналогічні теореми мають місце для границь функцій в точці.
Питання 24
Лемма о двух милиционерах — лемма в математическом анализе о существовании предела у функции, которая «зажата» между двумя другими функциями, имеющими одинаковый предел. Формулируется следующим образом:
Если
функция
|
