Визначення

Якщо K поле, а V є векторним простором над K. Зазвичай, елементи V називаються векторами, а елементи K називаються скалярами.

Якщо   є векторами, а   скалярами, тоді лінійною комбінацією векторів зі скалярними коефіцієнтами є

Лінійна залежність і незалежність векторів. Розклад вектора за базисом

З даного матеріалу Ви навчитеся розкладати вектор за базисом, перевіряти вектори на лінійну незалежність, знаходити вимірність простору. Почнемо вивчати з самого основного.

Нехай нам задано  вектори з  -вимірного векторного простору, а також деякі дійсні числа

Вектор

називається лінійною комбінацією векторів

Вектори бувають лінійно залежними або незалежними. Ці властивості визначають на основі наступних правил:

1) Вектори   називаються лінійно залежними, якщо знайдуться такі дійсні числа  , одночасно не рівні нулю, при яких справджується рівність

2) Якщо рівність

виконується лише за умови, що

то вектори називаються лінійно незалежними.

На практиці лінійну незалежність векторів перевіряють із умови, що визначник складений із координат векторів відмінний від нуля. Для приладу, якщо маємо три вектори з простору  , то для підтвердження їх лінійної незалежності визначник

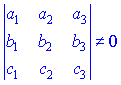
не має бути рівний нулеві. В іншому випадку вектори будуть лінійно залежними.

З властивостей визначників випливає, що вектори  будуть лінійно залежні тоді і тільки тоді, коли хоча б один з них є лінійною комбінацією інших.

Вимірність простору - це максимальна кількість лінійно незалежних векторів, що може бути у ньому. Будь-яку сукупність  лінійно незалежних векторів  -вимірного лінійного простору   називають його базисом.

Будь-який вектор з   єдиним способом може бути зображений у вигляді лінійної комбінації векторів базису. Якщо   - базис лінійного простору  , то   - розклад вектора за базисом  ,

- координати вектора   у цьому базисі.

Задачі розкладу вектора займають важливе місце в курс вищої математики, і потрібні не менше за відшукання базису лінійного простору.

------------------------------------

Алгоритм розкладу вектора за базисом

1. Записати рівність  у матричній формі. Вектори   подати у вигляді матриць-стовпців.

2. Матричне рівняння записати у вигляді системи лінійних алгебраїчних рівнянь. Розв'язати одержану систему.

3. Записати розклад вектора   за базисом  .

Для цього в рівність

замість   підставити розв'язки системи рівнянь

----------------------------------

Приклад 1.

Записати розклад вектора   за базисом

Розв'язок.

Скористаємося формулою розкладу вектора

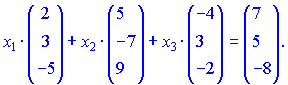
Дане рівняння записуємо у вигляді системи лінійних рівнянь

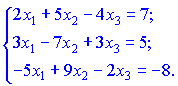
Розв'язком цієї системи 

Отримані значення підставляємо в рівняння розкладу, в результаті отримаємо  - розклад вектора   в базисі 

Як бачите обчислення не складні, наведена інструкція допоможе Вам розв'язати подібні задачі.

Питання 11  (1) можлива при деяких ненульових коефіцієнтах, то вектори   називають лінійно залежними. Якщо ж дана рівність виконується тільки при нульових коефіцієнтах, то вектори   називають лінійно незалежними. Розглянемо деякі твердження, які дають можливість давати відповідь на питання про лінійну залежність чи незалежність векторів без використання означення.

Базисом (дав.-гр. βασις, основа) векторного простору L називається впорядкований набір векторів {e₁, …, e_n} , якщо кожний вектор із Lможна однозначно представити у вигляді лінійної комбінації:

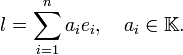
Ранг системи векторів — найбільше число лінійно-незалежних векторів з цієї системи. Приклади.

Питання 12

4.1 Різні види рівнянь прямої на площині. Пряма на площині геометрично може бути задана різними способами: точкою і вектором, паралельним даній прямій; двома токами; точкою і вектором, перепендикулярним до даної прямої, тощо. Різним способам завдання прямої відповідають у прямокутній системі координат різні види її рівнянь. 1) Аx+Вy+С=0 – загальне рівняння. 

Питання 13

Взаємне розташування прямих.

Дві прямі на площині можуть:

• збігатися;

• бути паралельними (тобто не перетина­тися);

• мати одну спільну точку.

(Дійсно, якщо б дві прямі могли мати хоча б дві спільні точки, то через ці дві точки проходили б дві різні прямі, що суперечить аксіомі І, п. 2).

Питання 14

Загальне рівняння кривої другого порядку:

Ах2 + 2Вху + Су2 + Бх + Еу + Е = 0 являє собою коло, якщо коефіцієнти при квадратах координат рівні між собою А = С, і якщо відсутній член з добутком координат ху, тобто В = 0.

Питання 15