Алгоритм[ред. • ред. Код]

1. Обирається перша зліва колонка, що містить хоч одне ненульове значення.

2. Якщо верхнє число у цій колонці - нуль, то обмінюється увесь перший рядок матриці з іншим рядком матриці, де у цій колонці нема нуля.

3. Усі елементи першого рядка діляться на верхній елемент обраної колонки.

4. Від рядків, що залишились, віднімається перший рядок, помножений на перший елемент відповідного рядка, з метою отримання у якості першого елемента кожного рядка (крім першого) нуля.

5. Далі, повторюємо ці операції із матрицею, отриманою з початкової матриці після викреслювання першого рядка та першого стовпчика.

6. Після повторення операцій n-1 разів отримаємо верхню трикутну матрицю.

7. Віднімаємо від передостаннього рядка останній рядок, помножений на відповідний коефіцієнт, щоб у передостанньому рядку залишилась лише 1 на головній діагоналі.

8. Повторюємо попередній крок для наступних рядків. У результаті отримуємо одиничну матрицю і рішення на місці вільного вектора (над ним необхідно виконувати ті самі перетворення).

9. Ме́тод Га́уса — алгоритм розв'язку системи лінійних алгебраїчних рівнянь.

10. Початок алгоритму.

11. Прямий хід: Шляхом елементарних перетворень рядків (додавань до рядка іншого рядка, помноженого на число, і перестановок рядків) матриця приводиться до верхньотрикутного вигляду(ступінчатого вигляду).

12. З цього моменту починається зворотний хід.

13. З останнього ненульового рівняння виражаємо кожну з базисних змінних через небазисні і підставляємо в попередні рівняння. Повторюючи цю процедуру для всіх базисних змінних, отримуємофундаментальний розв'язок.

14. Метод Крамера (Крамера правило) — спосіб розв'язання квадратних систем лінійних алгебраїчних рівнянь із ненульовим визначником основної матриці (при цьому для таких рівнянь розв'язок існує і є єдиним). Метод було створено Габріелем Крамером у 1750 році.

15. Опис методу[ред. • ред. Код]

16. Для системи   лінійних рівнянь з   невідомими (над довільним полем)

17. 

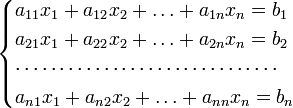
18. з визначником матриці системи 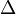 , що не рівний нулю, розв'язок записується у такому вигляді:

19. 

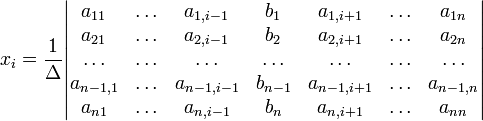
20. (i-й стовпчик матриці системи замінюється стовпчиком вільних членів). Іншим чином правило Крамера формулюється так: для будь-яких коефіцієнтів c₁, c₂, …, c_n виконується рівність:

21. 

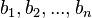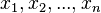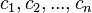22. У такій формі формула Крамера справедлива без припущення, що   не рівне нулю, не треба навіть, аби коефіцієнти системи були елементами цілісного кільця (визначник системи навіть може бути дільником нуля у кільці коефіцієнтів). Також можна вважати, що або набори   та  , або набір   складаються не з елементів кільця коефіциєнтів системи, а деякого модуля над цим кільцем. В такому вигляді формула Крамера використовується, наприклад, при доведенні формули для визначника Грама і Леми Накаями.

Питання 10.

Вектори.Лінійна комбінація системи векторів,розклад вектора за іншими векторами.

Геометричний вектор — у фізиці і математиці — величина, яка характеризується числовим значенням і напрямком. У фізиці існує чимало важливих величин, котрі є векторами, наприклад сила, положення, швидкість, прискорення, кутовий момент, імпульс, напруженість електричного і магнітного полів. Їх можна протиставити іншим величинам, таким, як маса, об'єм, тиск, температура та густина, які можна описати звичайним числом, їх називають «скалярами».

інійна комбінація — сума із декількох математичних об'єктів одного типу, кожен з яких є попередньо помноженим на довільну скалярну константу, одне з основних понять в лінійній алгебрі.