Питання 1

Матриця — математичний об'єкт, записаний у вигляді прямокутної таблиці чисел (чи елементів кільця), він допускає операції (додавання, віднімання, множення та множення на скаляр). Зазвичай матриці представляються двовимірними (прямокутними) таблицями. Іноді розглядають багатовимірні матриці або матриці непрямокутної форми.

Множення на число

Якщо дано матрицю A і число c, можемо означити множення на скаляр cA як (cA)[i, j] = cA[i, j]. Наприклад,

З цими двома операціями множина M(m, n, R) усіх матриць m-на-n з дійсними елементами є дійсним векторним простором розмірності mn.

Додавання

Якщо дано дві матриці m-на-n A і B, можемо означити їх суму A + B як матрицю m-на-n, що утворюється додаванням відповідних елементів, себто, (A + B)[i, j] = A[i, j] + B[i, j]. Наприклад,

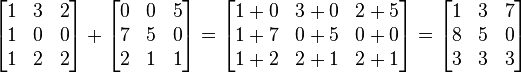
Множення матриць

Множення двох матриць має сенс лише тоді, коли число стовпчиків першої матриці дорівнює числу рядків другої матриці. Якщо A — матриця m-на-n (m рядків, nстовпчиків), а B — матриця n-на-p (n рядків, p стовпчиків), їх добуток AB є матрицею m-на-p (m рядків, p стовпчиків), що розраховується за формулою:

(AB)[i, j] = A[i, 1] * B[1, j] + A[i, 2] * B[2, j] + ... + A[i, n] * B[n, j] для кожної пари i та j.

Наприклад,

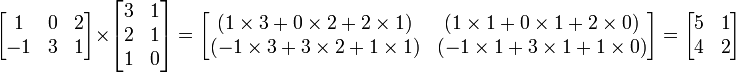
Питання 2

Одинична матриця — квадратна матриця розміру   з одиницями на головній діагоналі та нулями у всіх інших елементах.

Зазвичай позначається як  , іноді з індексом, що вказує розмірність:  .

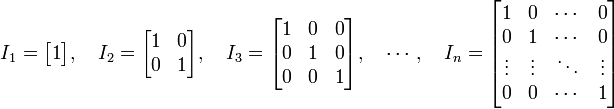
В лінійній алгебрі нульова матриця — матриця всі елементи якої рівні нулю. Приклади нульових матриць:

Множення одиничну матрицю 

5	6
7	8

Дано:

Матрица |A| :

5 6 7 8

Матрица |B| :

1 0 0 1

Найти матрицу |C| = |A| x |B| =

Питання 3 Транспонована матриця

Матеріал з Вікіпедії — вільної енциклопедії. Перейти до: навігація, пошук Транспонована матриця — матриця A^T, що виникає з матриці A в результаті операції транспонування: заміни її рядків на стовпчики. Формально, транспонована матриця  для матриці  визначається як Наприклад:      та      

 Діагональна – елементи поза головною діагоналлю нульові, на головній – будь-які. Наприкалад, матриця

1) Квадратні   та прямокутні матриці  . Наприклад,

 – прямокутна матриця;

 – квадратна матриця.

5) Верхня трикутна (нижня трикутна ) матриця – елементи під діагоналлю (над діагоналлю) в таких матрицях нульові. Наприклад,

Верхня трикутна – 

Нижня трикутна 

У випадку, коли елементи головної діагональні в трикутній матриці одиничні її називають унітрикутною

Визначник або детермінант — вираз складений за певним законом з n² елементів квадратної матриці. Одна з найважливіших характеристик квадратних матриць.

Для квадратної матриці розміру   визначник є многочленом степеня   від елементів матриці, і є сумою добутків елементів матриці зі всіма можливимикомбінаціями різних номерів рядків і стовпців (в кожному із добутків є рівно по одному елементу з кожного рядка і кожного стовпця). Кожному добутку приписується знак плюс чи мінус, в залежності від парності перестановки номерів.

Якщо елементами матриці є числа, то визначник — також число. Взагалі, визначник може бути функціональним або належати якомусь комутативному кільцю, залежно від походження матриці.

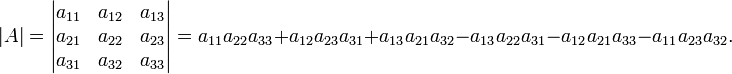
Ви́роджена ма́триця (особли́ва, сингуля́рна, неінверто́вана) — квадратна матриця, визначник якої дорівнює нулю:

Неви́роджена ма́триця (неособли́ва, несингуля́рна, інверто́вана) — квадратна матриця, визначник якої не дорівнює нулю:

Питання 4

1. Якщо помножити якийсь рядок на константу 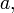  то визначник також помножиться на 

2. Якщо у матриці поміняти місцями будь-які два рядки, то знак визначника зміниться на протилежний.

3. При додаванні до будь-якого рядка лінійної комбінації кількох інших рядків визначник не зміниться.

4. У матриці з двома однаковими/пропорційними рядками або з нульовим рядком, визначник дорівнює нулю.

5. Всі властивості визначників, що стосуються рядків, так само справедливі і для стовпців.

6. Визначник трикутної матриці дорівнює добутку елементів на діагоналі.

7. Теорема Лапласа: визначник квадратної матриці дорівнює сумі добутків елементів деякого рядка на відповідні їм алгебраїчні доповнення.

8. Лема про фальшивий розклад: сума добутків елементів деякого рядка на алгебраїчні доповнення відповідних елементів паралельного рядка дорівнює нулю.

9. 

10. 

11. 

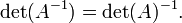
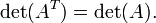
Питання 5

Обернена матриця,її існування та єдність Обернена матриця — матриця (позначається  ), яка існує для кожної невиродженої квадратної матриці , розмірності  , причому:

де   одинична   матриця.

Якщо для матриці   існує  , то така матриця називається оборотною, тобто кожна невироджена матриця є оборотною, і навпаки — кожна оборотна матриця є невиродженою.

Питання 6

Матричні рівняння та методи їх розв’язування

Питання 7

Ранг Матриці . Приклади