1.3. Приклад виконання обробки результатів прямих вимірювань з багаторазовими спостереженнями

При проведенні міжлабораторних випробувань виникає специфічна модель вимірювань, звана гніздовою структурою [3]. Особливістю цих вимірювань є те, що вони проводяться в різний час, різними засобами вимірювань, в різних умовах, різними методами, різними операторами. При цьому утворюється кілька груп прямих вимірювань з багаторазовими спостереженнями, які для зменшення невизначеності слід об'єднувати, отримуючи єдиний результат вимірювання. З огляду на те, що невизначеності (дисперсії) спостережень у кожній із груп мають різне значення, визначення сумарної невизначеності об'єднаного результату вимірювань необхідно проводити з урахуванням математичного апарату, званого дисперсійним аналізом.

Кількість факторів визначається числом рівнів «гніздування». Під фактором розуміють відмінність в умовах проведення груп спостережень. Ним може бути день, в який проводилися вимірювання, прилад або метод вимірювань, оператор, місце проведення вимірювань і т.д.

Розглянемо найпоширенішу на практиці найпростішу модель врівноваженої одноетапної гніздової структури.

Нехай є J груп прямих багаторазових спостережень величини Y з K спостережень у кожній групі. Алгоритм обробки результатів цих спостережень полягає в наступному.

1. Визначаються середні арифметичні кожної групи спостережень:

(1.9)

де y_jk означає k - те спостереження величини Y (k = 1, 2 ,..., К) в j-й групі (j = 1, 2 ,...,J).

2. Визначається середнє арифметичне отриманих середніх арифметичних y_j, приймається за найкращу оцінку вимірюваної величини Y:

(1.10)

3. Обчислюється оцінка внутрішньогрупової дисперсії в j-ій групі (число таких дисперсій дорівнює кількості груп J):

(1.11)

4. Знаходиться експериментальна дисперсія середніх арифметичних груп:

(1.12)

Така оцінка тільки одна.

5. Визначається, чи є міжгрупових складова дисперсії значною в порівнянні з внутрігруповою складовою. Для цього виконують такі операції.

5.1. Визначають дві незалежні оцінки усередненої внутрішньогрупових дисперсії спостережень.

Перша оцінка, позначена як s₁², виходить із спостережуваних відхилень щоденних середніх арифметичних у_j (1.9). Оскільки у_j, є середнє арифметичне K спостережень, його оцінена дисперсія s²(у_j) при допущенні, що міжгруповa дисперсія дорівнює нулю, оцінюється як s₁²/К. Тоді з рівняння (1.11) випливає

(1.13)

Ця оцінкою має (j-1) ступенів свободи.

Друга оцінка, позначена як s²_II, є середньою оцінкою дисперсії, отриманої з J індивідуальних значень внутрішньогрупової дисперсії s²_j(у_jk):

(1.14)

Оскільки структура врівноважена і всі ступені свободи ν_j=К-1, то виходить що в результаті вираз для s²_II є просто середнє арифметичне s²_j (у_jk):

(1.15)

Таким чином, з урахуванням виразу (1.11), отримують:

(1.16)

що є оцінкою, що має J(К-1) ступенів свободи.

Оскільки оцінка s₁² грунтується на мінливості середніх арифметичних, в той час як оцінка s_II² грунтується на мінливості усередині групових спостережень, їх відмінність показує можливу присутність (міжгрупової) мінливості.

5.2. Порівнюють значення s₁² і s_II². Для цього використовують F - тест.

Відомо, що F - розподіл складових є розподілом ймовірностей відношення:

(1.17)

двох незалежних оцінок s₁²(ν₁) і s_II²(ν_II) дисперсії нормально розподіленої випадкової змінної. Параметри v₁ і v_II являются відповідні ступені свободи двох оцінок, а 0≤F(v₁, v_II)<∞. Критичні значення F для різних ймовірностей (квантами F - розподілу) внесені в таблицю розподілу Фішера для різних значень v₁ і v_II (див. додаток Б).

Зазвичай критичні значення F задаються для ймовірностей 0,95, 0,975 або 0,99. Якщо розраховане значення F(v₁, v_II) більше, ніж критичний для заданої ймовірності (F_0.95, F_0.975 або F_0.99), то це повинно тлумачитися як наявність міжгрупової дисперсії, оскільки s₁²(ν₁) більше s_II²(ν_II) на статистично значиму величину.

6. При F(v₁, v_II)<F_p коли існування міжгрупової похибки заперечується, тому що різниця між s₁² і s_II² не розглядається як статистично значуща, оцінену дисперсію для y слід вирахувати із загального виразу:

(1.18)

Це співвідношення еквівалентно рівнянню:

(1.19)

Дійсно, можна переписати вираз (1.19) як:

В отриманому виразі:

З урахуванням цього отримуємо вираз (1.20).

Таким чином, якщо припустити, що всі поправки на систематичні ефекти враховані і всі інші складові невизначеності незначні, то результат вимірювання можна отримати як

із сумарною стандартною невизначеністю s(у) (4.26), що має JK-1 ступенів свободи.

Розширену невизначеність результату вимірювання можна розрахувати за формулою

де t_p (ν) - коефіцієнт Стьюдента для числа ступенів свободи v=JK-1 та рівня довіри р. Для v> 30 замість коефіцієнта Стьюдента можна брати коефіцієнт охоплення для нормального закону розподілу.

7. При F(v₁, v_II)≥F_р існування міжгруповий дисперсії приймається (розумне рішення, оскільки воно дозволяє уникнути можливої недооцінки невизначеності) і передбачається, що вона випадкова. Тоді оцінена дисперсія у виходить з s² (у_j), так як вона належним чином відображає як внутрішньогрупову, так міжгрупову випадкові складові дисперсії. Таким чином,

і з урахуванням рівняння (4.19), отримуємо

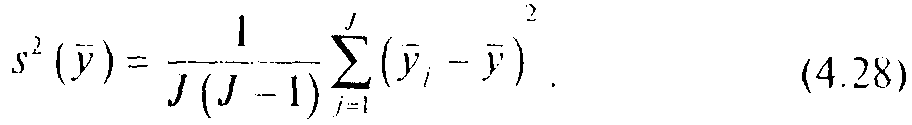
Ця оцінка дисперсії має J - 1 ступенів свободи.

Розширену невизначеність результату вимірювання можна розрахувати за формулою

де t_p – коефіцієнт Стюдента для числа степенів вільності ν=J-1 та рівня довіри p.