2.5 Определение статической характеристики преобразования измерительного преобразователя

2.5.1 Аппроксимация схп

Статическую характеристику преобразования ИП аппроксимируют на основании полученных оценок средних арифметических значений объединённой группы результатов равноточных из­мерений (усреднением 20 измеренных значений, соответствующих од­ному значению входного напряжения) или по средневзвешенным значениям при неравноточных измерениях.

Если результаты двух групп объединить нельзя (так как группы из­мерений неоднородны), то необходимо установить функциональную зависимость характеристики преобразования ИП для каждой группы результатов отдельно, а оценки погрешностей ИП определить с учётом требования метрологической надёжности.

Построить график эксперимента­льно полученной функции СХП вида у = f (x), т.е. Ū_{вых j} = f (U_вх), и по внешнему виду графика функции предложить гипотезу о математической зависимости, которой можно описать данное соотношение.

Для нахождения аппроксимирующей функции применяют метод наименьших квадратов (МНК). По виду графика экспериментальной СХП задают математическую функцию аппроксимирующего полинома начиная с более простой (с учётом принципа максимального правдоподобия), например в виде линейной зависимости y = a + bx или Ū_вых = а + bU_вх.

В соответствии с выбранным видом полиномиальной модели со­ставляют систему условных уравнений, учитывая количество точек контроля по диапазону:

Количество условных уравнений избыточно (n = 11), так как превышает число неизвестных (коэффициенты a и b). Поэтому необходимо перейти к системе нормальных уравнений, для которой количество неизвестных и количество уравнений равно. Решение условных уравнений должно быть таким, чтобы сумма квад­ратов невязок была минимальной (постулат Лежандра):

Для линейной аппроксимирующей зависимости нормальные уравне-ния имеют вид

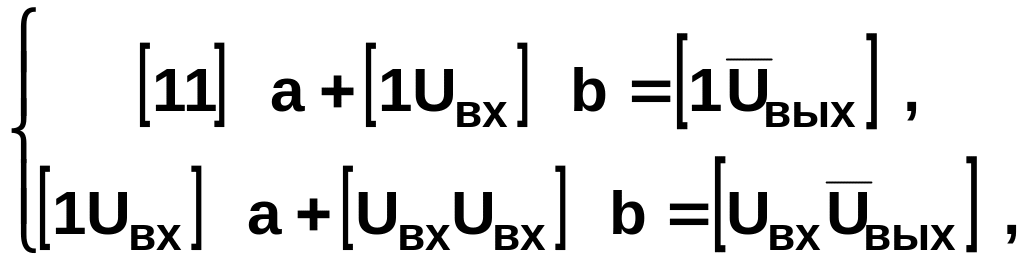
где

Решение нормальных уравнений можно получить методом опре­дели-телей:

и найти оценки коэффициентов

Необходимо представить уравнение модели аппроксимирующего (расчетного) полинома СХП, определить значения U_{вых. аппр j} аппроксимирующей СХП и невязки условных уравнений:

= U_{вых. аппр j} – Ū_{вых. эксп j} .

Результаты занести в табл. 2.11.

Таблица 2.11 – Характеристики СХП

Uвх 0	Uвх 1	Uвх 2	Uвх 3	Uвх 4	Uвх 5	Uвх 6	Uвх 7	Uвх 8	Uвх 9	Uвх 10
Ūвых. эксп 0	…	…	…	…	…	…	…	…	…	Ūвых. эксп 10
Ūвых. аппр 0	…	…	…	…	…	…	…	…	…	Ūвых. аппр 10
0	…	…	…	…	…	…	…	…	…	10