2.4 Определение закона распределения случайных измерений

Определить закон распределения выборочных значений можно с по­мощью гистограмм, применив критерий согласия Пирсона.

Сначала строят гистограмму, отображающую распределение резуль-татов случайных измерений, полученных экспериментально, затем –расчётную (теоретическую) гистограмму.

Так как результаты наблюдений получены для различных значений входного сигнала, то определять закон распределения случайных величин нужно по случайным отклонениям :

1. Расположить случайные отклонения объединенных ре­зультатов (без промахов) в вариационный ряд – от наименьшего значения до наибольшего с учетом знака. Привести вариационный ряд в табл. 2.10.

Таблица 2.10 - Вариационный ряд случайных отклонений

	…	…	…	…	…	…	…	…	…
…	…	…	…	…	…	…	…	…	…
…	…	…	…	…	…	…	…	…

2. Вычислить среднее арифметическое и оценку СКО слу­чайных отклонений, а также диапазон значений слу­чайных отклонений .

3. Определить шаг h , задавшись числом интервалов к (от 7 до 13):

.

4. Найти границы полуоткрытых к-интервалов кото-рые будут определять масштаб гистограммы по оси абсцисс. Прибавляя значение шага h к , получаем верхнюю гра­ницу первого полуоткры-того интервала; к концу первого интервала, прибавляя значение шага, найдём верхнюю границу второго интервала и т.д. Привести значения границ интервалов.

5. Рассчитать серединные значения каждого из к-интервалов:

6. Определить нормированные средние значения каждого интер­вала:

7. Найти значения функции плотности вероятностей нормированного нормального распределения (см. табл. П.Б.4) или рассчитать по формуле

Так как функция определена в области положительных значений, то полученную числовую оценку нужно удвоить.

8. Вычислить количество случайных отклонений, которые по­пали бы в каждый полуоткрытый интервал (общее количество интервалов к), если бы распределение подчинялось стандартному нормальному (гауссовому)

где N – общее (совокупное) количество оцениваемых случайных отклонений;

h – шаг гистограммы;

– СКО случайных отклонений.

9. Построить экспериментальную и теоретическую гистограммы.

На оси абсцисс определить диапазон отклонений и обозначить границы интервалов. По оси ординат отложить количество случайных n_i и стандартных отклонений n_iст, попавших в каждый интервал.

Например, получены такие гистограммы (рис. 2.2), где сплошной линией показана гистограмма, построенная по экспериментальным значениям, а пунктирной – теоретическая гистограмма.

n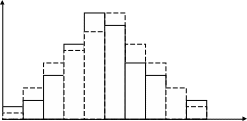 _i и n_iст

к (= 10)

Рисунок 2.2 – Гистограммы распределений

Из рис. 2.2 видно, что экспериментальная и теоретическая гисто-граммы не совпадают, но количественную оценку этого несовпадения можно рассчитать с помощью критерия Пирсона (см. п. 10).

Если в одном или нескольких интервалах не окажется ни одного случайного отклонения, то интервалы необходимо расширить (или сузить), т.е. уменьшить (или увеличить) их количество и пересчитать оценки. По результатам построить гистограммы. Отсутствие случайных отклонений в интервалах может указывать на пропущенный недостовер-ный результат, поэтому рекомендуется выполнить проверку на промахи по критерию Смирнова (см. табл. П.Б.1) или Граббса.

В некоторых случаях указанная рекомендация не приводит к ожидаемому результату. Тогда нужно применить метод усечения, который заключается в исключении (отбрасывании, усечении выборки) одинаково-го количества случайных отклонений с начала (слева) и с конца (справа) вариационного ряда и пересчёте всех оценок с построением новых гисто-грамм (см. пп.1 - 9).

10. Определить меру расхождения между оцениваемым и теорети-ческим (стан­дартным) распределениями по всем к-интервалам, применив интегра­льный критерий согласия Пирсона:

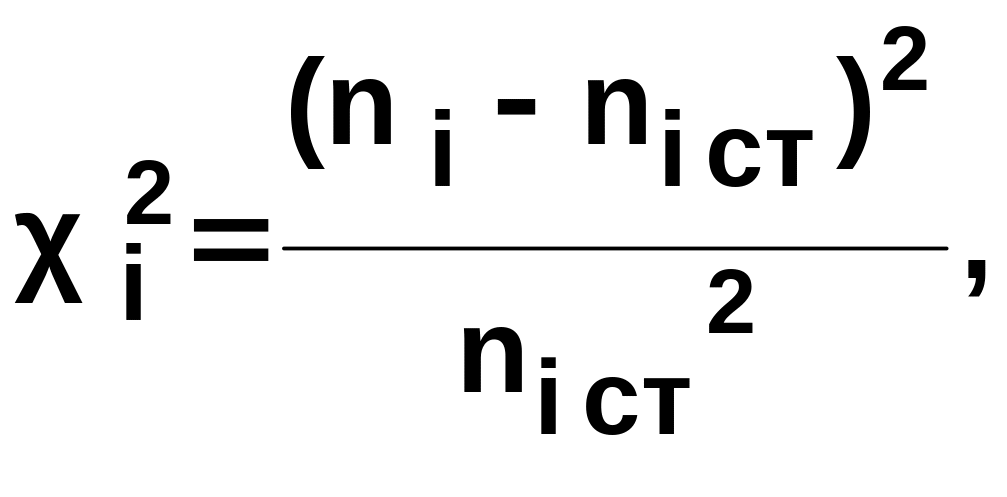
где n_i и n_iст – количество случайных отклонений и стандартных откло­нений, попавших в каждый интервал.

Интегральную оценку во всем диапазоне случайных отклонений получить путём суммирования -оценок: . Задавшись уров­нем значимости q, доверительной вероятностью Р_дов (q + Р_дов = 1) и числом сте­пеней свободы k = к – 3 (к – количество интервалов, 3 – число ограничений для нормального стандартного распределения), найдём по таблице критерия Пирсона (см. табл. П.Б.9) нижнюю и верхнюю допус­тимые границы функции . Если , то распределение случайных отклонений и результатов измерений подчиняется нормальному закону.

Если критерий не выполняется, т.е. или , то рас-пределение результатов измерений нельзя считать нормальным (гауссовым). Тогда по виду экспериментальной гистограммы необхо­димо подобрать максимально правдоподобную функцию и по крите­рию Пирсона подтвердить выбранную гипотезу, задавшись видом функции соответствующего распределения.