2.3 Объединение результатов групп измерений

2.3.1 Проверка на однородность

Назначение – проверить, какой характер имеет расхождение средних значе­ний измерения выходного напряжения при одном и том же значении входного напряжения – систематический или случайный. Для этого нужно проверить результаты измерений на однородность по Т-кри­терию (критерию Стьюдента):

;

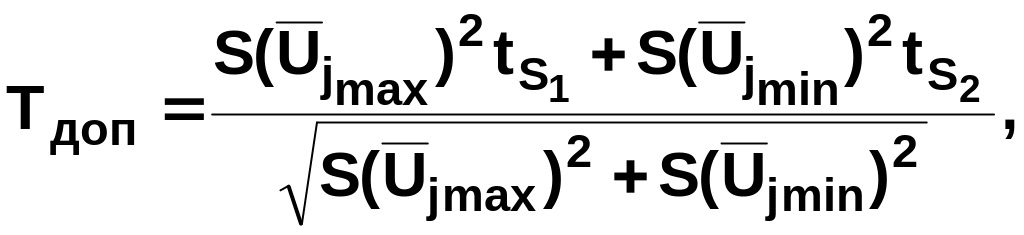
где и – коэффициенты Стьюдента (выбирают из таблицы статистики Стьюдента в зависимости от значения доверительной ве­роятности Р_дов и числа степеней свободы k₁ = n₁ – 1 и k₂ = n₂ – 1, см. табл. П.Б.2);

n₁ и n₂ – количество результатов наблюдений в каждой группе для одного значения входного сигнала.

Результаты вычислений представить в табл. 2.6.

При < (критерий сходится) максимальное расхождение средних значений признают случайным, систематическую состав­ляющую погрешности – несущественной, а результаты измерений, полученные для одного значения входного сигнала, можно объеди­нить в один ряд.

Допустимо, если Т-кри­терий не сходится по одному-двум значениям входного сигнала. Тогда следует повысить значение Р_дов вплоть до 0,99 и снова выполнить проверку. При сходимости критерия можно считать однородность для указанных значений малодостоверной.

Если разность наибольшего и наименьшего средних значений больше допустимого, т.е. > , то результаты – неоднородны (из-за система­тической составляющей погрешности) и объединяться не могут. В этом случае необходимо ввести поправку в результаты измерений .

Таблица 2.6 - Результаты проверки на однородность

Uвх i	Uвх 0	Uвх 1	Uвх 2	Uвх 3	Uвх 4	Uвх 5	Uвх 6	Uвх 7	Uвх 8	Uвх 9	Uвх 10
	…	…	…	…	…	…	…	…	…	…	…
	…	…	…	…	…	…	…	…	…	…	…
Вывод	…	…	…	…	…	…	…	…	…	…	…

Поправка может быть аддитивной (рис. 2.1, а) при смещении характерис­тики преобразования на постоянное значение Δ_адд = а = соnst, мультипликативной (рис. 2.1, б) Δ_мульт = bх или смешанной (рис. 2.1, в) Δ = Δ_адд + Δ_мульт = а + bх.

Δ_адд = а = соnst Δ_мульт = bх Δ = а + bх

а б в

Рисунок 2.1 – Соотношения СХП результатов двух серий измерений

Для установления характера поправки нужно построить СХП двух групп из­мерений в одних координатах и по соотношению полученных графи­ков сделать вывод (см. рис. 2.1), после чего рассчитать и ввести поправочный коэффициент в оценки результатов измерений . После введения поправки выполнить проверку по Т-критерию. Результаты вычислений представить в таблице, аналогичной табл. 2.6.

Если после введения поправки Т-критерий не сходится, то результаты следует обрабатывать для каждой группы измерений отдельно. В этом случае проверки на равноточность и независимость результатов измере-ний двух групп не имеют смысла. В противном случае необходимо провести эксперимент заново, увеличив группы измерений до трёх-четырёх, и выполнить все вычисления сначала.