2.2 Определение погрешности гистерезиса и вариации схп

Погрешность гистерезиса обусловлена упругим несовершенством элементов измерительного преобразователя и численно определяется как алгебраическая разность значений выходного сигнала для одного и того же значения входного сигнала при плавном возрастании и плавном умень-шении входного сигнала в заданном диапазоне. При многократных измерениях абсолютные значения погрешностей гистерезиса при каждом значении входного напряжения выражают как разность средних арифметических значений прямого и обратного ходов:

,

где - САЗ в каждой контрольной точке диапазона измерения, определенное по результатам измерений, выполненных при прямом ходе (нечетные ряды);

- САЗ при обратном ходе (четные ряды);

j – количество точек контроля по диапазону измерения.

Определить абсолютные и относительныө погрешности для двух групп измерений и представить их в табл. 2.5:

.

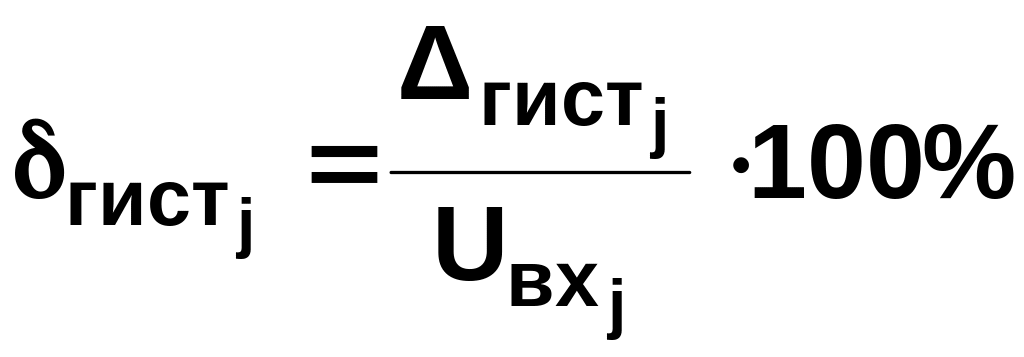Таблица 2.5 – Погрешности гистерезиса

Uвх 0	Uвх 1	Uвх 2	Uвх 3	Uвх 4	Uвх 5	Uвх 6	Uвх 7	Uвх 8	Uвх 9	Uвх 10
	…	…	…	…	…	…	…	…	…
	…	…	…	…	…	…	…	…	…
	…	…	…	…	…	…	…	…	…
	…	…	…	…	…	…	…	…	…
	…	…	…	…	…	…	…	…	…
	…	…	…	…	…	…	…	…	…
	…	…	…	…	…	…	…	…	…
	…	…	…	…	…	…	…	…	…

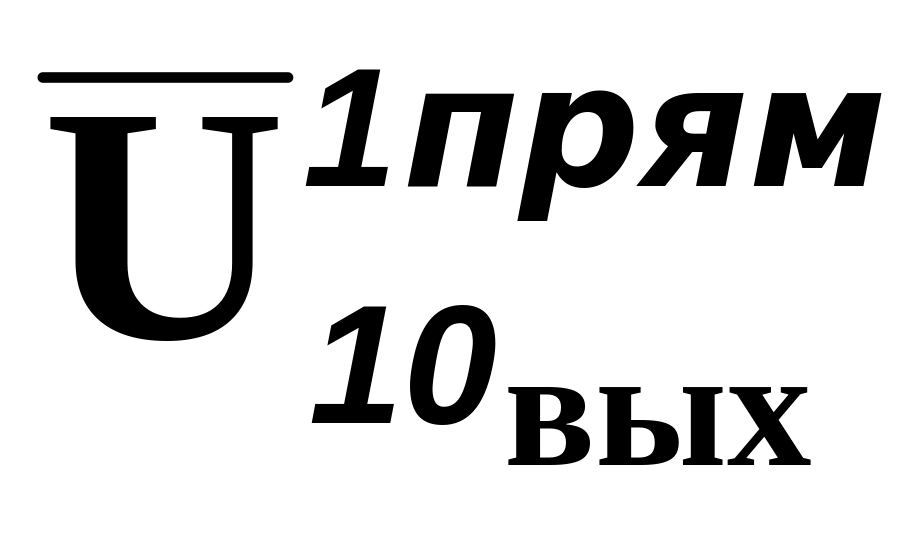
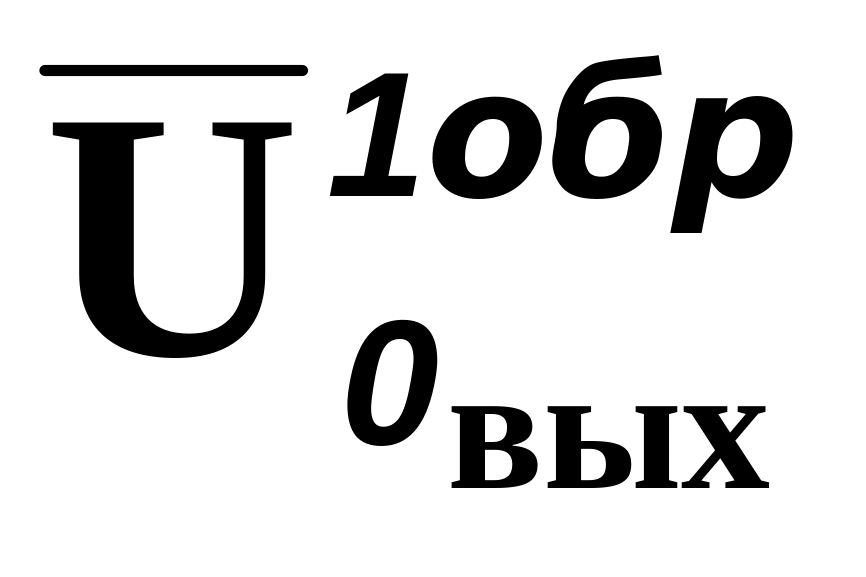
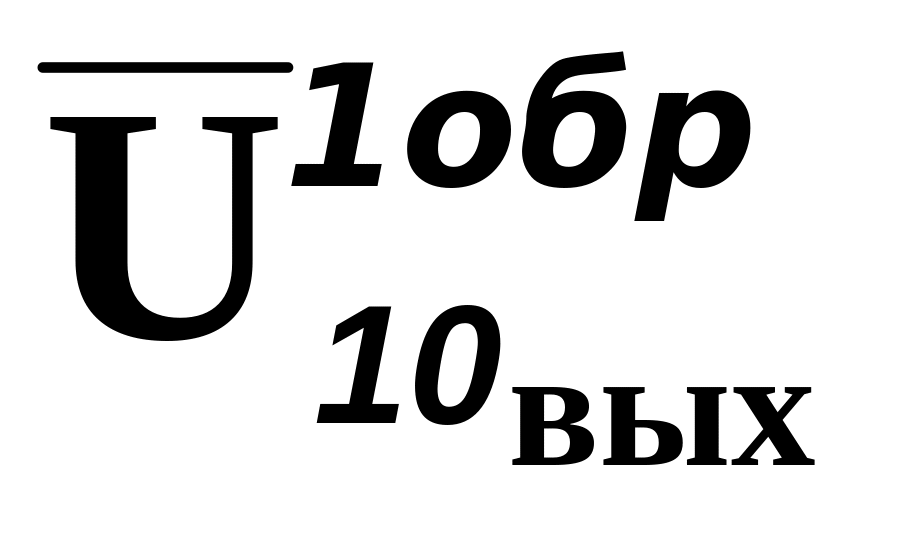
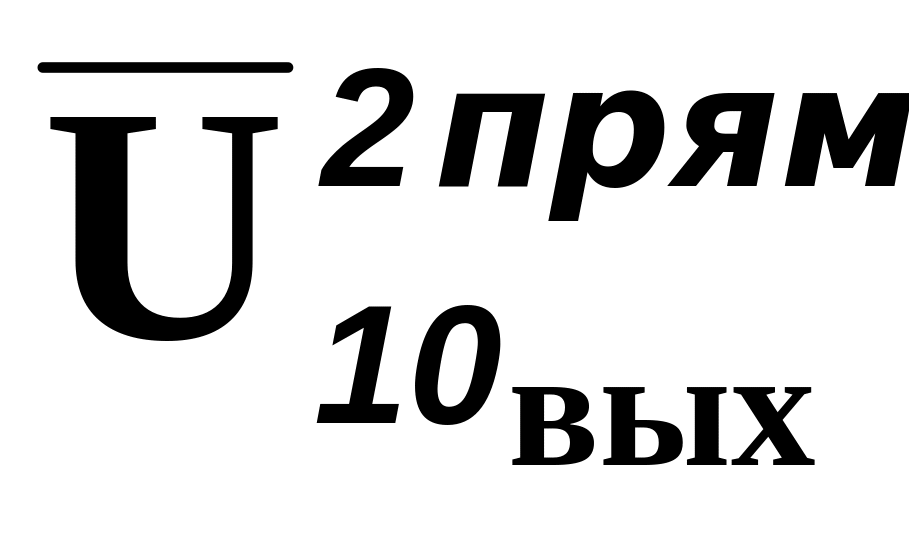
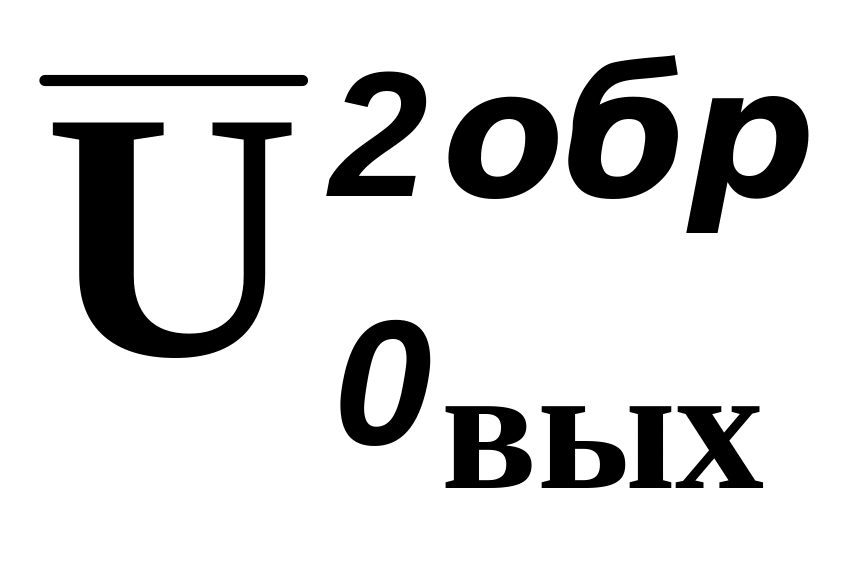
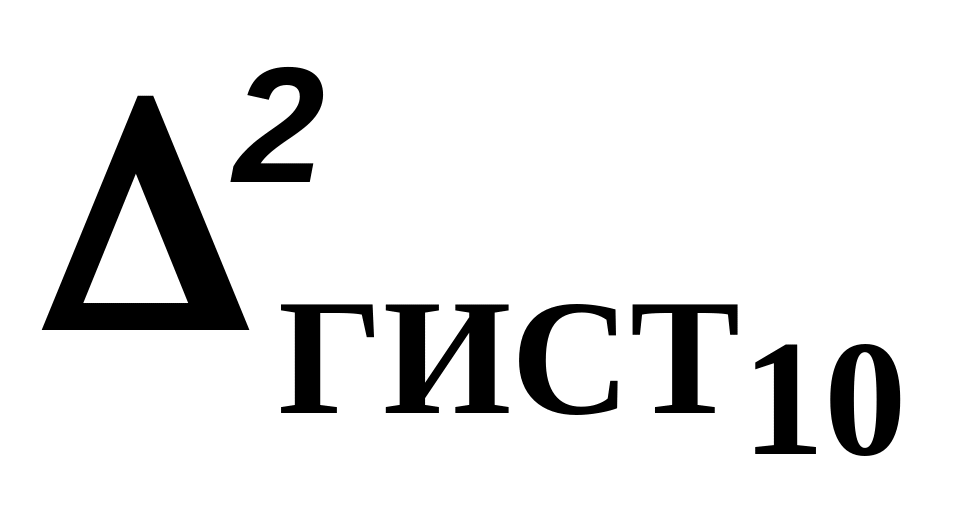
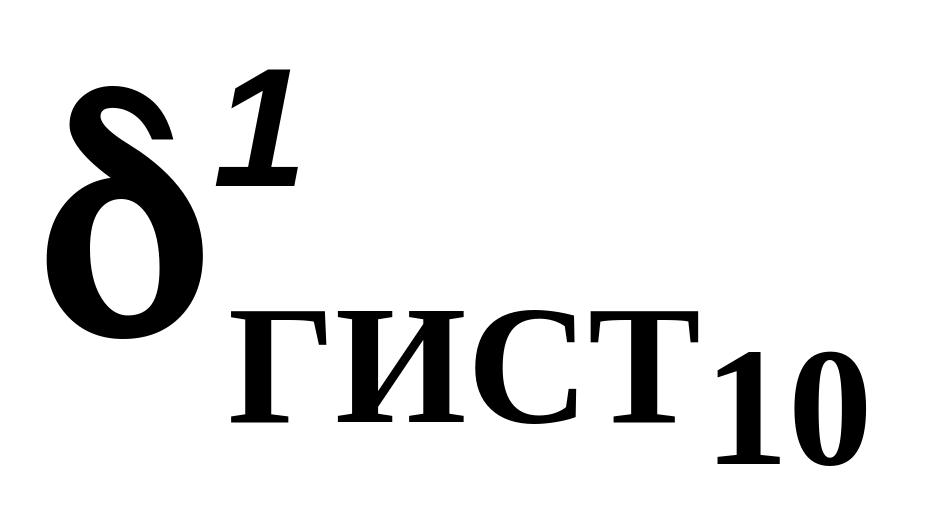
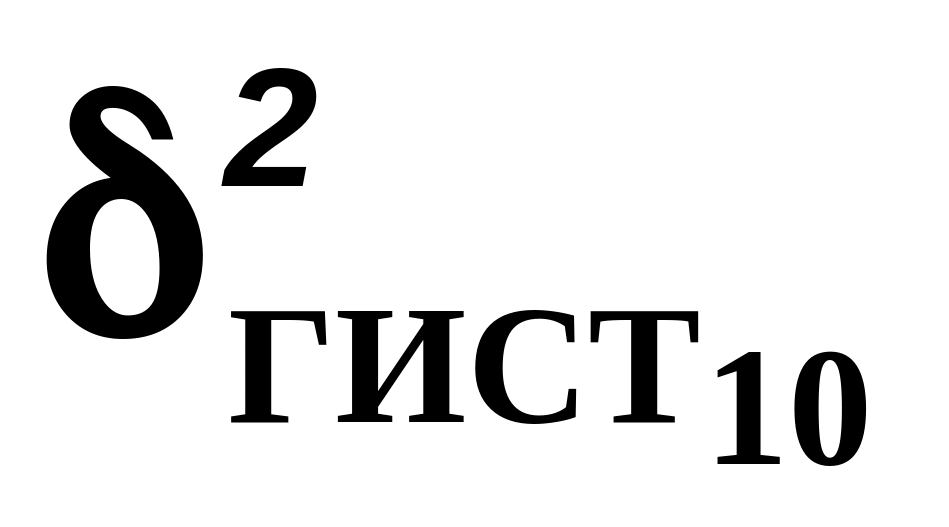
Вариацию СХП для каждой группы измерений определяют в виде приведенной погрешности

где - наибольшая абсолютная погрешность каждой СХП;

D – диапазон измерения входного сигнала.

Поскольку оценивают погрешность гистерезиса СХП одного и того же измерительного преобразователя, то из двух значений приведенной погрешности необходимо выбрать наибольшую и нормировать до стандартного значения из ряда

(1,0; 1,5; 2,0; 2,5; 3,0; 4,0; 5,0; 6,0)×10^p, где p = 2; 1; -1; -2; …