3.4.2 Обработка нескольких групп прямых многократных

из­мерений

Рассмотрим пример [2]. Выполняют калибровку эталона вольта с помощью стабиль­ного источника опорного напря­жения в течение нескольких не­дель. В каждый из j = 10 дней прово­дят K = 5 независи­мых повторных наблюдений разности потенциа­лов . Необхо­димо получить наилучшую оценку результата измере­ний и оце­нить ее неопределенность.

Предварительно обработанные результаты измерений пред­ставлены в табл. 3.2.

Таблица 3.2 – Результаты экспериментальных исследований

День j	1	2	3		4	5
	10,000172	10,000116	10,000013		10,000144	10,000106
	60	77	111		101	67
День j	6	7		8	9	10
	10,000031	10,000060		10,000125	10,000163	10,000041
	93	80		73	88	86

Определяют средние арифметические каждой группы наблюде­ний (см. табл. 3.2). Для измерений, выполненных в каждый из 10 дней ( обозначает і-е наблюдение разности потенциалов в -й день), имеем

Находят наилучшую оценку измеряемой величины как среднее арифметическое для всех :

Определяют оценки внутригрупповой дисперсии в каждой j-й группе (оценок – 10, результаты представ­лены в табл. 3.2):

Находят экспериментальную дисперсию средних ариф­метических групп (оценка – одна):

Рассчитывают две независи­мые оценки усредненной внутригрупповой дисперсии наблю­дений и , опре­деляющие, является ли межгрупповая составляющая дисперсии значи­тельной по сравнению с внутригрупповой со­ставляющей. Первую оценку ( ) получают из на­блюдае-мых отклоне­ний ежедневных средних арифмети­ческих . Поскольку – САЗ К-наблюдений, его оцененная дисперсия при допущении, что межгрупповая дисперсия равна нулю, оценивается как Следовательно,

Эта оценка имеет j - 1 = 9 степеней свободы.

Вторая оценка ( ) – средняя оценка дисперсии, полученная из J-индивидуальных зна­чений внутригруппо­вых дисперсий :

имеет j(K-1) = 40 степеней свободы.

Сравнивают значения и , применяя F-распределение вероятностей отношения двух независимых оценок и – дисперсий нор­мально рас­пределенной случайной переменной:

.

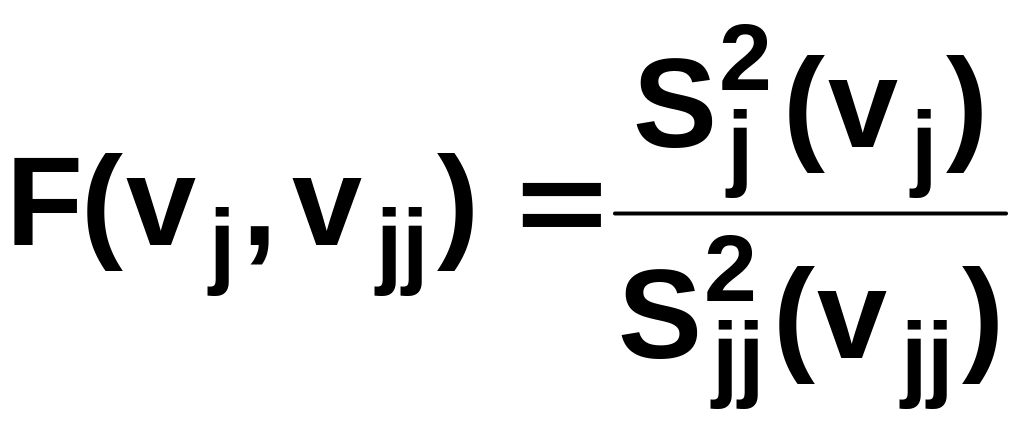Парамет­ры v_j и v_jj – соответствующие степени сво­боды двух оценок, а 0 ≤ F(v_j , v_jj) ≤ ∞ . Критические значе­ния F для различных вероятно­стей (квантили F-распре­деления) внесены в таблицу распределе­ния Фишера для разных значений v_j и v_jj .

Обычно критические значения задают для веро­ятностей 0,95, 0,975 или 0,99. Если рассчитанное значение F(v_j , v_jj) > F_P для заданной вероят­ности ( ), то это объясняют межгрупповой дисперсией, поскольку больше на статистически значимую величину. При F(v_j, v_jj) < F_P существование межгруп­повой дисперсии отрицают, так как разницу и не рассматривают как статистически значимую. Вычисляют значение

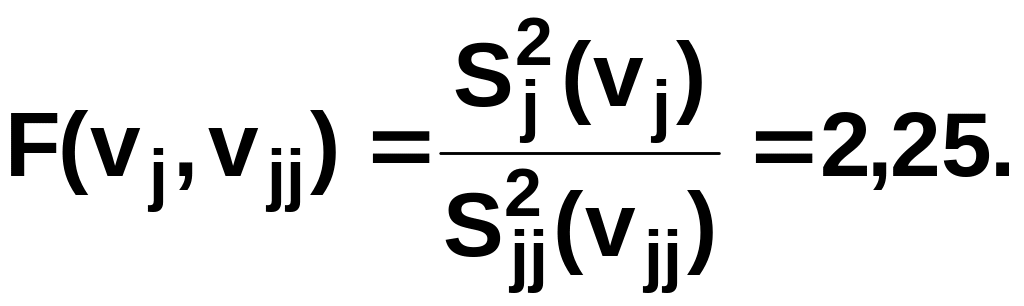
Критические значения F для вероятностей 0,95 и 0,975 и для числа степеней свободы v_j = 9 и v_jj = 40 находят по таблице распреде­ления Фишера: F_0,95 = 2,12; F_0,975 = 2,45 (см. табл. П.Б.7).

Для вероятности 0,975 F(v_j, v_jj) < F_P , поэтому существование межгрупповой дисперсии отрицают. В этом случае оцененную дис­персию для вычисляют так:

с jK-1 = 49 cтепенями свободы.

Расширенная неопределенность результата измерения

где k = 2 – коэффициент охвата для нормального закона рас­пределе­ния и уровня доверия р = 0,95.

Но для вероятности 0,95 при F(v_j , v_jj) ≥ F_P суще­ствование межгрупповой дисперсии принимается, а оцененная дисперсия для имеет вид

с степенями свободы.

Расширенную неопределенность результата измерения мож­но рассчитать как

где – коэффициент Стьюдента для числа степеней сво­боды v = J – 1 = 9 и уровня доверия Р = 0,95.