3.2.2.2 Коррелированные входные величины

Если входные величины коррелированы, то соответствующее выражение для суммарной дисперсии имеет вид

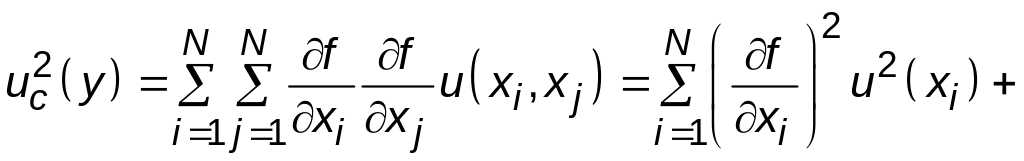(3.9)

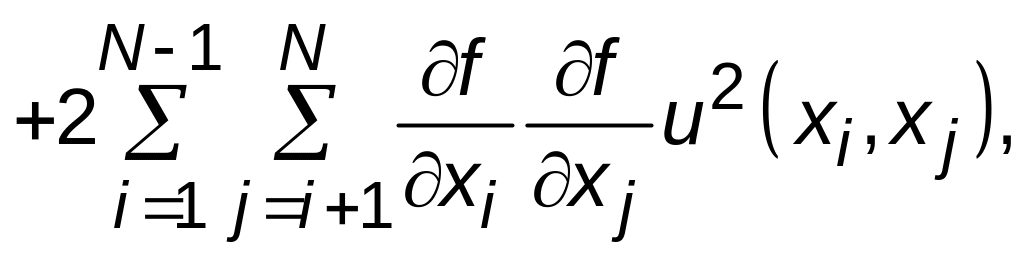
где х_і и х_j – оценки входных величин Х_і и Х_j;

– оцененная ковариация х_і и х_j.

Степень корреляции между х_і и х_j характеризуется коэффици­ен-том корреляции

(3.10)

где ;

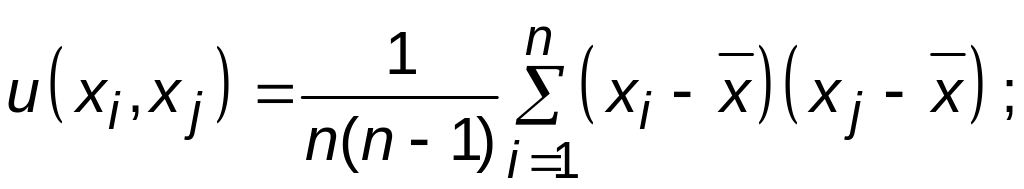
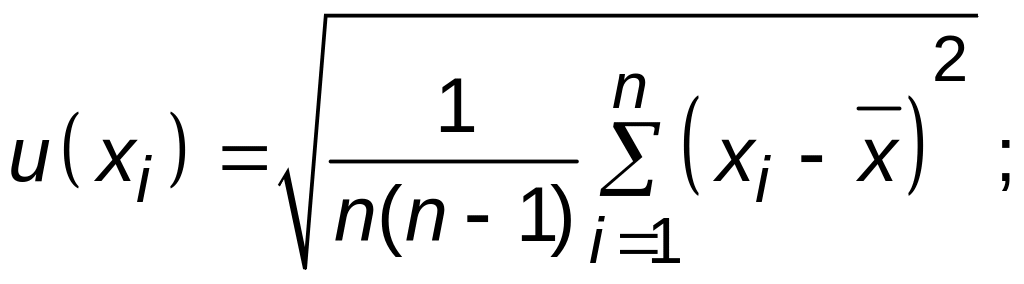
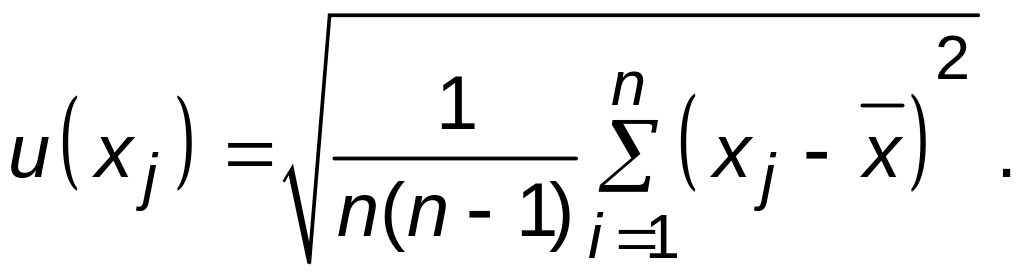
Таким образом, если имеются две случайно изменяющиеся ве­личины и n пар их одновременных наблюдений, то коэффициент кор­реляции между этими величинами вычисляют по формуле

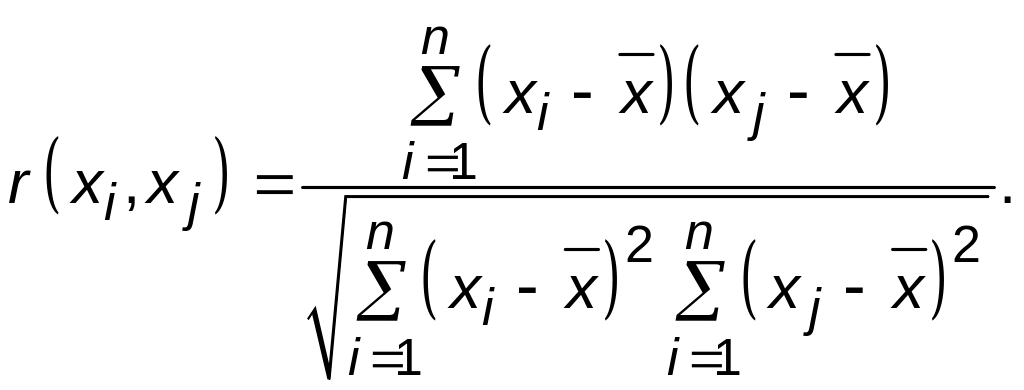(3.11)

Если оценки х_і и х_j независимы (корреляционной связи нет или она пренебрежимо мала), то

В терминах коэффициентов корреляции выражение для сум­марной дисперсии принимает вид

(3.12)

Cуммарная неопределенность оценки измеряемой величины Y:

(3.13)

Пример

Рассмотрим фрагмент описания лабораторной работы [3]. Изме-рим входную ёмкость вольтметра С_вх косвенным методом с использованием резонансного контура, резонансные частоты колебаний которого при отключенном вольтметре и подключенном являются исходными данными для статистической обработки и представляют собой исходные пары прямых многократных измерений.

Таким образом, имеем два ряда с одинаковыми количест­вами измерений для частот и , получен­ные в результате многократных измерений: f₁₁, f₁₂,..., f_1i,..., f_1n и f₂₁, f₂₂,..., f_2i,..., f_1n . Известно также аналитическое выражение, связывающее их с иско­мым параметром:

где – собственная начальная емкость резонансного контура.

Вычислим точечные оценки прямоиз­меренных величин в соответствии с формулами (3.1) и (3.2). Получим наиболее вероятные значения ре­зонансных частот , и их дисперсии , , по кото­рым

можно найти стандартные неопределенности типа А и .

Оценим действительное значение косвенной величины

Суммарную дисперсию оценки вычислим по формуле (3.12):

где – частные производные;

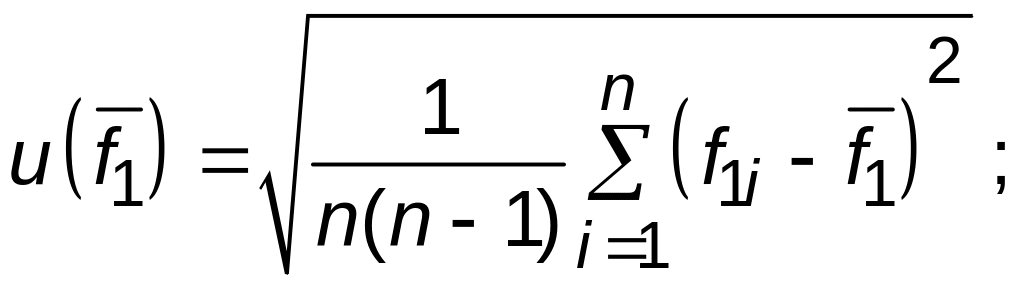
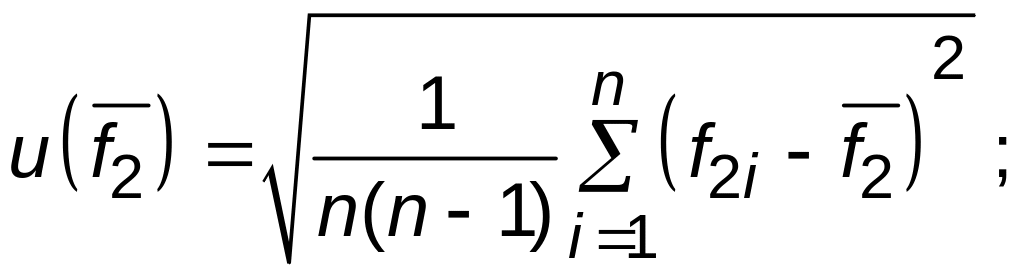
Рассчитаем по суммар­ной дисперсии суммарную неопределенность оценки :

.

3.2.3 Расширенная неопределенность

Международные документы по оцениванию неопреде­ленности в измерениях рекомендуют всем участникам при представлении ре­зультатов всех международных сличе­ний или других работ под эги­дой МКМВ и Консультатив­ных Комитетов использовать для выраже­ния достоверности измерения суммарную стандартную неопределен­ность [2]. Однако в отдельных случаях (торговле, про­мышлен­ности, здравоохранении и др.) и в регулирующих актах целесообразно допол­нительно указывать интервальную меру неопределенно­сти, которая называется расши­ренной неопределенностью и обозначается символом . Расширенная неопределённость выражает интер­вал для результата измере­ния, в пределах которого может нахо­диться бόльшая часть распределения значений с до-статочным основанием приписываемых измеряемой величине, и определяется путём умножения суммарной стандарт­ной неопределенности на коэффициент охвата :

(3.14)

При указании расширенной неопределенности ре­зультат измерения выражается как или и озна­чает, что наилучшей (вероятной, достоверной) оцен­кой значения величины Y является у, а ин­тервал от ( ) до ( ) содержит (по ожиданию) большую часть распределе­ния значений, которые можно с достаточным основа­нием приписать Y.

Чтобы получить значение коэффициента охвата k, определяющего интервал, соответствующий заданному уровню доверия P, необходимы точные сведения о законе распределения вероятностей, характеризующем рассеян­ность результата измерения.

Например, для величины у, распределённой по нормаль­ному за­кону, значения коэффициента охвата для разных уровней доверия приведены в табл. 3.1.

Если величину у описывают прямоугольным распре­делением вероятностей, то значение коэффициента охвата k = 1 для уровня доверия P = 57,74 %; k = 1,65 для Р = 95%; k = 1,71 для Р = 99% и k = для P = 1. Прямоугольное распре­деление «ỳже» нормального, так как обладает конечной протяженностью «хвостов».

Таблица 3.1 – Коэффициент k для нормального распределения

P,%	68,27	90	95	95,45	99	99,73
k	1	1,645	1,96	2	2,576	3

Если закон распределения величины у неизвестен, то, имея ре­зультаты многократных ее измерений, можно оп­ределить эксперимен­тальный закон распределения и идентифицировать его по известному теоретическому.