Предисловие

Современные средства измерительной техники позволяют получить большие объёмы измеренных значений за короткие промежутки времени. Последующее усреднение измеренных значений существенно уменьшает влияние случайной составляющей погрешности на точность результата измерений и создаётся впечатление, что путём увеличения числа измерений и опытов можно значительно повысить точность измерений. Но при этом игнорируются присутствие в каждом опыте неисключённых систематических, методических и дополнительных погрешностей, коррелированность результатов измерений и другие причины, оказывающие влияние на точность измерений. Очевидно, что необходимо так построить измерительный эксперимент и последующую обработку измеренных значений, чтобы при сравнительно небольших объёмах измерений можно было получить оптимальные по точности и числу измерений оценки. В частности, изучив и применив оптимальную методику обработки результатов нескольких групп многократных измерений, можно ощутимо повысить достоверность полученных результатов при сохранении единообразия оценок их точности.

В работе даны рекомендации по выбору необходимых и достаточных критериев оценивания параметров одной из важнейших метрологических характеристик средств измерений – статической характеристики преобразования, описана методология расчёта для типовых вариантов характеристик преобразования и представлено обоснование определения макси-мально правдоподобной номинальной функции преобразования для измерительного преобразователя с применением метода наименьших квадратов.

В разд. 3 приведены теоретические сведения, практические рекомендации и примеры оценивания неопределённостей результатов многократных измерений в соответствии с «Руководством по выражению неопределённости измерений».

В Приложения включены таблицы различных распределений случайных величин, наиболее часто применяемые в практике инженера-метролога, и необходимые для выполнения как курсовой работы (проекта), так и текущих заданий по ряду дисциплин.

Авторы убеждены, что учебное пособие поможет студентам-метрологам выполнять домашние, курсовые и выпускные работы, а студентам других специальностей – более полно и глубоко освоить ряд специальных знаний по метрологии и измерительной технике.

1 Цель, задачи и условия выполнения эксперимента

Цель работы – освоение методики обработки нескольких групп результатов прямых многократных измерений на примере выполнения эксперимента по получению характеристик исследуемого средства измерения (СИ) – измерительного преобразова­теля (ИП) – и определения его статической характеристики преоб­разования (СХП).

СХП называют измеренную в статическом режиме зависимость выходного сигнала ИП (измеренное напряжение) от входного сигнала (измеряемое напряжение. Определив вид математической модели этой зависимости, можно найти функцию ИП. На рис. 1.1 показана функциональная схема установки для проведения эксперимента.

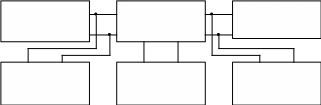
Задающий Измерительный Активная

генератор преобразователь нагрузка

Аналоговый Источник Цифровой

вольтметр питания вольтметр

Рисунок 1.1 – Функциональная схема измерительной установки

Чтобы оцениваемые результаты измерений были достоверны, надежны и правильны характеристику преобразо­вания измеряют дважды, выполняя прямые многократные измерения.

Первую группу измерений получают, изменяя входное напряже­ние ИП в заданном диапазоне с постоянным шагом при неизменном значении частоты синусоидального напряжения генератора. Входной сигнал измеряют с помощью аналогового вольт­метра, а выходной – посредством цифрового вольтметра. Результаты измерений записывают в табл. 1.1.

Аналогично первой группе измерений через 30 - 40 мин получают вторую группу измерений. Разделение во времени позволяет оценить стабильность характеристик ИП. Со­противление нагрузки ИП в процессе измерений остаётся неизмен­ным. Если результаты измерений второй группы существенно (более чем на 5 %) отличаются от результатов первой группы, то нужно получить третью группу измерений.

Установку на время перерыва от электропитания не отключать!

Рекомендуемая методика получения результатов измерений:

1. Установить на шкале частот генератора синусои­дальных сиг­налов заданную частоту, выбрать необходимый предел измерения напряжений. На передней панели аналогового вольтметра устано­вить переключатель на измерение гармонического сигнала, найти поддиапазон измеряемого напряжения и выбрать шкалу отсчета показа­ний. На передней панели цифрового вольтметра установить соответ­ствующие род работы и под-диапазон измерения выходного напряжения. Установить переключатель напряжений источника питания в положение «15 В» (при ступенчатой регулировке) и в поло­жение, соответствующее примерно ½ диапазона (при плавной регу­лировке).

Пригласить преподавателя для проверки правильности установок режима измерения.

2. Включить питание приборов.

3. Выполнить калибровку вольтметров.

4. На вход ИП от задающего генератора, последовательно уве­ли-чивая значения начиная с нуля, подавать напряжение в заданном диапа-зоне, изменяя его на постоянное значение (шаг). Входное напряжение для ИП измерять аналоговым вольтметром, а выходное – цифровым.

Результаты попарно измеренных значений входного и выходного напряжений ИП записать в табл. 1.1. Так как измеряемые значения вход­ного сигнала контролируют по шкале аналогового вольтметра (на­ибольшая погрешность установки равна ½ цены деления шкалы), то повторять запись значений входного напряжения в табл. 1.1 нет необ­ходимости.

5. На вход ИП от задающего генератора подавать напряжение в заданном диапазоне, последовательно уменьшая значения от наибо­льшего до нуля, изменяя его на постоянное значение (шаг), т.е. второй проход по диапазону измерения реализуется по тем же значениям входного сигнала. Результаты измеренных значений выходного на­пряжения ИП записать в табл. 1.1.

6. Повторить измерения при плавном увеличении входного на­пряжения до максимального (возрастающие значения), а затем уменьшая напряжение от наибольшего к минимальному (убывающие значения), не менее 10 раз.

Таким образом, каждый нечетный ряд (1, 3, 5, 7, 9 строки таблицы результатов наблюдений) будет характеризовать возрастающие значения напряжения (прямой ход измерений), а каждый четный ряд (2, 4, 6, 8, 10 строки) – убывающие значения (обратный ход).

7. Получив результаты первой группы измерений, не отключая приборы от сети, сделать перерыв на 30 - 40 мин и повторить измерения. Результаты наблюдений второй группы записать в табл. 1.2.

Условия получения результатов измерений:

1. Входное напряжение – U_{вх. нач}, В - ____ ; U_{вх. конечн}, В - ____ _.

2. Диапазон измеряемого напряжения – D = U_{вх. конечн} - U_{вх. нач}, В - ___ _.

3. Частота входного напряжения – Гц - _______ _.

4. Шаг изменения входного напряжения – В - _____ _.

5. Перерыв между группами измерений, мин - _______ _.

Таблица 1.1 – Результаты первой группы измерений

Uвх j , В
Uвых, В
Uвых 1, В
Uвых 2, В
Uвых 3, В
Uвых 4, В
Uвых 5, В
Uвых 6, В
Uвых 7, В
Uвых 8, В
Uвых 9, В
Uвых 10, В

Таблица 1.2 – Результаты второй группы измерений

Uвх j , В
Uвых, В
Uвых 1, В
Uвых 2, В
Uвых 3, В
Uвых 4, В
Uвых 5, В
Uвых 6, В
Uвых 7, В
Uвых 8, В
Uвых 9, В
Uвых 10, В

Результаты получены _______ (дата) ___________ (ФИО) ________ (подпись)

Преподаватель __________________ (должность, ФИО) ___________ (подпись)

Задачи, решаемые в курсовой работе:

1. Определение оценки наиболее вероятного значения как среднего арифметического значения (САЗ) выходного сигнала для каждого значения входного сигнала.

2. Нахождение случайных отклонений результатов наблюдений квадратов случайных отклонений, оценки среднего квадратического отклонения и дисперсии результатов наблюдений и результатов измерений.

3. Проверка результатов наблюдений на наличие «промахов» по критериям Смирнова (или Граббса) и 3 («три сигма»).

4. Определение однородности групп измерений по критерию Стьюдента (Т-критерий).

5. Определение равнорассеянности дисперсий и равноточности результатов групп измерений по критерию Фишера (F-критерий).

6. Определение (не)зависимости результатов групп измерений и существенности корреляционной связи по R-критерию.

7. Определение соответствия результатов измерений теоретическому закону распределения по составному d-критерию, параметрическим критериям и интегральному критерию Пирсона.

8. Определение погрешностей от гистерезиса (абсолютных, относительных и приведенных).

9. Аппроксимация СХП методом наименьших квадратов, опреде-ление оценок и неопределенностей коэффициентов теоретической модели СХП.

10. Аппроксимация невязок методом наименьших квадратов, определение адекватности теоретической модели СХП результатам измерений.

11. Расчет оценок аддитивной и мультипликативной составляющих основной погрешности ИП, погрешности нелинейности номинальной СХП и класса точности ИП.

12. Привести (оценить) стандартную, суммарную, расширенную и относительную неопределенности.