МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Казанский Национальный Исследовательский Технический Университет им. А. Н. Туполева(КНИТУ-КАИ)

Институт Радиоэлектроники и Телекоммуникации (ИРЭТ)

Кафедра Радиоэлектроники и Квантовых Устройств (РЭКУ)

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

«Исследование частотно-модулированного автогенератора(чмаг)»

Лабораторная работа № 306

Составили:

Профессор д.ф.-м.н. Шахмаев М.М.

Ст.преподаватель каф. РЭКУ Гимадеева Л.А.

Макетирование, настройка

и оформление документации

студент гр. 5505 Бизяев А.В.

студент гр. 5503 2009г. Ахметов Т.А.

студенты гр. 5503 2011г (осень) Даутов А.Л.

Гайнанов Р.Э.

студенты гр. 5201 – 2011г. Назарьев П.Н.

Закиров И.Р.

Музафарзода И.М.

Казань2011

Цель работы

Исследование и изучение схем частотной модуляции.

1. Основные понятия и определения

В технике радиосвязи и радиовещания частотная модуляция (ЧМ) получила всеобщее признание. Частотная модуляция позволяет получить выигрыш в помехоустойчивости за счет использования широкой полосы частот при сравнительно несложной аппаратуре и существенных эксплуатационных преимуществах. Она применяется при УКВ вещании, в системах УКВ связи (в том числе с подвижными объектами),на большинстве радиорелейных линий связи и линий связи через искусственные спутники Земли.

Любая величина (ток, напряжение, напряженность поля), гармонически изменяющаяся во времени, описывается выражением

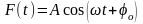(1.1)

где - амплитуда колебаний,

ω- круговая (циклическая) частота колебаний,

- начальная фаза колебаний,

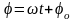- мгновенное значение фазы колебаний

При постоянных значениях амплитуды , частоты , фазы колебание, определяемое соотношением (1.1) не может быть использовано для передачи информации. При изменении , , в соответствии с сигналом информации передача сообщения возможна, в этом случае 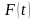называют модулированным высокочастотным сигналом, а сигнал информации - модулирующим сигналом.

При изменении частоты колебаний по закону модулирующего сигнала получаем частотно-модулированное колебание (ЧМК). В самом общем виде ЧМК описывается уравнением вида

(1.2)

где

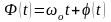
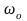- частота колебаний при отсутствии модулирующего сигнала:

- функция, определяющая частотную модуляцию.

Для модулированного колебания называется мгновенным фазовым углом. Для получения неискаженной передачи сигнала мгновенная фаза должна быть медленно меняющейся функцией по сравнению с функцией .

Физический смысл этого ограничения заключается в том, что за период высокочастотного колебания модулирующий сигнал не должен сильно измениться (практически модулирующий сигнал за время должен остаться постоянным).

Известно, что между фазой колебания 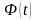и круговой частотой имеется следующая дифференциальная связь

(1.3)

При частотной модуляции частота колебаний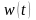 должна изменяться по закону модулирующего сигнала, т.е.

(1.4)

где - коэффициент пропорциональности,

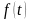- модулирующий сигнал.

В этом случае в соответствии с (1.4) и (1.3) выражение (1.2) для ЧМК будет иметь вид

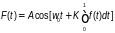(1.5)

Если модулирующий сигнал гармонический ( ), то мгновенная частота колебаний будет иметь вид

, а уравнение для ЧМК согласно (1.5)

(1.6)

В этом уравнении

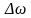- девиация частоты, пропорциональная амплитуде модулирующего сигнала, т.е.

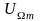- амплитуда модулирующего колебания.

Отношение определяет девиацию фазы при частотной модуляции. Это отношение называют индексом частотной модуляции и обозначают буквой , стало быть