Формула для обчислення мішаного добутку векторів, які задані своїми координатами у правому ортонормованому базисі
Покажемо,
як визначити мішаний добуток векторів
,
знаючи координати цих векторів у правому
ортонормованому базисі
:
,
,
.
Маємо на підставі (7.2)
.
Розкладаючи визначник за елементами першого рядка, одержимо
.
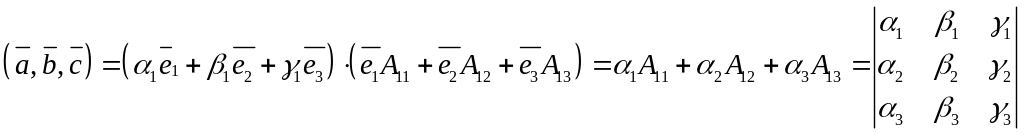Отже,
,
(8.1)
де
– координати вектора
в ортонормованому правому базисі,
– координати вектора
у тому ж базисі, а
– координати вектора
.
Приклад.
В ортонормованому правому базисі
задані вектори
,
,
.
З'ясувати, чи є трійка векторів
правою. Знайти об’єм
паралелепіпеда, який побудовано на цих
векторах.
Розв’язання. Обчислимо мішаний добуток векторів за формулою (8.1)
.
Оскільки
,
то за властивістю 2 мішаного добутку,
трійка векторів
– права і об’єм
паралелепіпеда, який побудовано на
векторах
дорівнює
.
На
закінчення параграфу розглянемо випадок,
коли базис
векторного простору довільний
(необов’язково ортонормований) і в
цьому базисі
,
,
.
Одержимо формулу для обчислення мішаного
добутку
.
Будемо виходити з означення:
.
Розглянемо вектор
:
.
Тепер маємо
Таким чином, мішаний добуток векторів , , з відомими координатами в будь-якому базисі векторного простору можна обчислити за формулою
.
(8.2)
Для
правого ортонормованого базису, очевидно,
=+1
(паралелепіпед, побудований на одиничних
векторах правої трійки
,
є куб з об’ємом V=1).
В цьому випадку формула (8.2) перетворюється
у формулу (8.1) для обчислення мішаного
добутку векторів з відомими координатами
у правому ортонормованому базисі.
З формули (8.2) і властивості 1 мішаного добутку векторів випливає справедливість такого твердження: вектори компланарні тоді й тільки тоді, коли їх координати в деякому базисі векторного простору обнуляють визначник у формулі (8.2), тобто, якщо у деякому базисі векторного простору , , , то необхідна і достатня умова компланарності цих векторів така:
.