Формула для обчислення векторного добутку векторів, які задані своїми координатами у правому ортонормованому базисі

Нехай – правий ортонормований базис і нехай у цьому базисі відомі координати двох векторів і . Визначимо координати вектора .

За означенням координат вектора у базисі маємо:

, .

Отже,

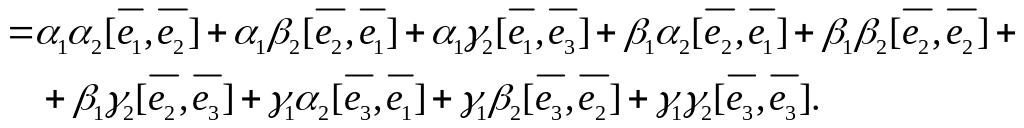
Приймаючи до уваги формули (7.1), одержимо після приведення подібних членів

.

Отримали формулу для обчислення векторного добутку векторів, які задані своїми координатами у правому ортонормованому базисі. Легко побачити, що її можна записати у такому вигляді

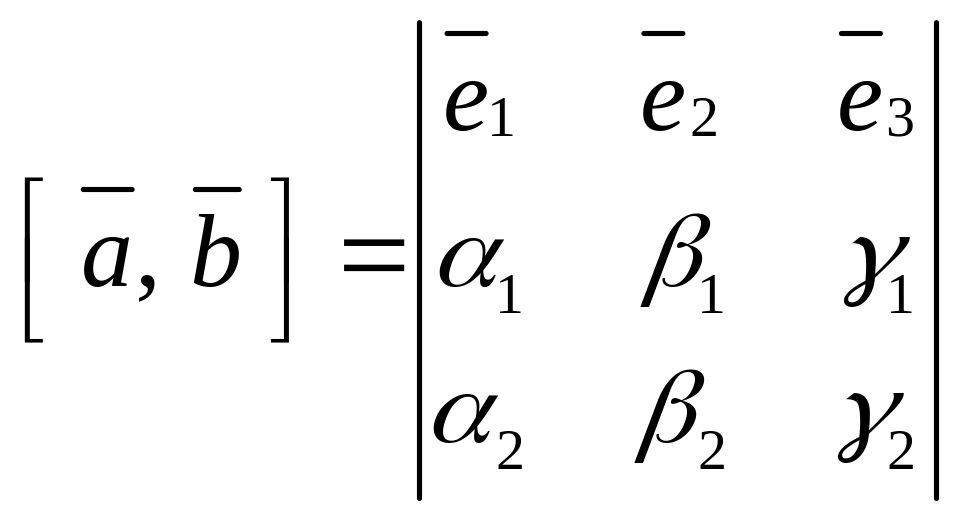. (7.2)

Порівнюючи дві останні формули для вектора , приходимо до висновку, що координати вектора дорівнюють алгебраїчним доповненням елементів першого рядка визначника (7.2), тобто

.

Приклад. Обчислити площу паралелограма, який побудовано на векторах та . Координати векторів і задані у правому ортонормованому базисі .

Розв’язання. У випадку правого ортонормованого базису має місце формула (7.2), за якою:

.

У такий спосіб . Визначимо модуль вектора або, що те ж саме, шукану площу паралелограма

( ).

Означення 3.7.2. Вектор називають подвійним векторним добутком векторів .

Якщо вектори та – неколінеарні та вектор не є ортогональним векторам і , то, як видно з рисунку 3.8, вектор лежить у площині векторів і , тобто є їх лінійною комбінацією (теорема 3.3.3): .

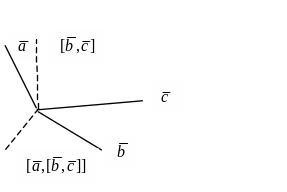
Рис.3.8. Подвійний векторний добуток

Більш досконалий аналіз дозволяє встановити, що

.

Для полегшення запам'ятовування цієї формули зручно користуватися таким мнемонічним правилом: подвійний векторний добуток векторів дорівнює «бац» мінус «цаб».

§ 3.8. Мішаний добуток трьох векторів

Означення 3.8.1. Мішаним добутком векторів називають число .

З означення мішаного добутку випливають наступні його властивості.

Властивість 1. Мішаний добуток дорівнює нулю тоді й тільки тоді, коли один з векторів дорівнює нулю або всі три вектори паралельні одній площині, тобто компланарні.

Дійсно, якщо один з векторів дорівнює нулю, то очевидно, що . Якщо ж три ненульових вектори компланарні, то ясно, що (або , якщо ║ ), тому .

Навпаки, якщо , то можливі такі варіанти:

1) один з векторів дорівнює ,

2) вектори – ненульові, але ║ ,

3) вектори – ненульові при цьому , тобто паралельні одній площині.

У другому та третьому випадках вектори – компланарні. Таким чином, якщо , то або один з векторів нульовий, або ненульові вектори – компланарні. 

Властивість 2. Мішаний добуток трьох відмінних від нульового вектору некомпланарних векторів за абсолютним значенням дорівнює об’єму паралелепіпеда, який побудовано на векторах . При цьому, якщо трійка векторів – права, то , якщо ж вона – ліва, то . Вірно й зворотне твердження.

Рис.3.9. Паралелепіпед, що побудовано на векторах

 Нехай – права трійка векторів (рис. 3.9), тоді кут між векторами і є гострим і тому . Відомо з § 3.7, що є площа паралелограма, який побудовано на векторах і , тобто площа основи паралелепіпеда. Висота паралелепіпеда, як видно з малюнку 3.9, дорівнює . Таким чином, об’єм паралелепіпеда дорівнює . Звідки за означенням скалярного та мішаного добутків векторів . Отже, якщо трійка векторів є правою, то

.

Аналогічним чином можна переконатися, що у випадку лівої трійки векторів об’єм паралелепіпеда, побудованого на цих векторах, обчислюється за формулою

.

Методом доведення від супротивного легко перевірити, якщо , то трійка векторів – права, якщо ж , то трійка – ліва.

Властивість 3. При циклічному переставленні векторів у мішаному добутку останній не змінюється, тобто . При переставленні двох будь-яких сусідніх векторів у мішаному добутку останній змінює знак, тобто

.

Легко переконатися за допомогою малюнка 3.9, що при циклічному переставленні некомпланарних векторів орієнтація нової трійки залишається незмінною, тобто якщо вона була, наприклад, до переставлення правою, то й після переставлення залишається правою. Але тоді за властивістю 2 мішаного добутку . При переставленні двох будь-яких векторів у некомпланарній трійці векторів орієнтація нової трійки буде протилежною по відношенню до вихідної трійки. Тому за властивістю 2 мішаного добутку векторів .

Примітка. Доведенні рівності вірні також у тому випадку, коли вектори компланарні, бо в цьому випадку =0.

Властивість 4. Для будь-яких векторів та для будь-яких дійсних чисел та вірні рівності:

,

,

.

Наведені формули є наслідком аналогічних властивостей скалярного та векторного добутків.