§ 3.6 Скалярний добуток двох векторів

Означення 3.6.1. Скалярним добутком двох ненульових векторів та називається число, яке дорівнює добутку довжин векторів, що перемножуються, на косинус кута між ними:

.

Якщо хоча б один з векторів або є нульовим, тоді вважають . Іноді для скалярного добутку користуються іншим позначенням: . З означення скалярного добутку двох векторів випливають наступні його властивості.

Властивість 1. Скалярний добуток комутативний. Для будь-яких векторів та :

.

Властивість 2. Скалярний добуток довільного вектора на себе дорівнює квадрату довжини цього вектора:

.

Відзначимо, що скалярний добуток прийнято називати скалярним квадратом вектора та позначати: . Внаслідок властивості 2 скалярного добутку

.

Властивість 3. Для будь-яких векторів та : , якщо .

 За теоремою 3.5.4 . Помножимо обидві частини цієї рівності на модуль вектора , одержимо

.

Таким чином, . Очевидно, при .

Властивість 4. Для будь-яких векторів та та для будь-якого дійсного вірні рівності

.

 Якщо один з векторів або є нульовим, то твердження теореми справедливо. Нехай та ненульові вектори, тоді за властивістю 3 скалярного добутку та за теоремою 3.5.3 (властивість проекцій) маємо

.

У силу комутативності скалярного добутку: .

Властивість 5. Якщо та – довільні ненульові вектори та , то та – ортогональні.

 Нехай – кут між векторами та . За умовою . Оскільки і , то . В області функція лише при . Отже, вектори і ортогональні. 

Властивість 6. Для будь-яких векторів та :

.

 При зазначена рівність виконується. Нехай , тоді за властивістю 3 скалярного добутку векторів . За теоремою 3.5.2: , тому .

Наслідок. Для будь-яких векторів та : .

У § 3.4 було показано, що будь-які три некомпланарні вектори можуть утворювати базис у тривимірному векторному просторі.

Означення 3.6.2. Якщо базисні вектори – одиничні (довжини дорівнюють одиниці) та попарно ортогональні, то базис називається ортонормованим.

Ортонормований базис може бути правим або лівим.

Означення 3.6.3. Відкладаємо вектори ортонормованого базису з однієї точки О простору. Будемо прагнути, повертаючи вектор навколо точки О у площині векторів і сполучити його з вектором . Із двох напрямків обертання варто обрати той, якому відповідає найменший кут повороту. Якщо для спостерігача, що дивиться з кінця вектора на площину векторів і , зазначений поворот вектора відбувається проти ходу годинникової стрілки, то базис вважається правим. У супротивному випадку базис – лівий. На малюнках зображені правий і лівий ортонормовані базиси.

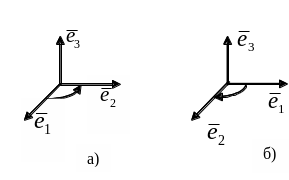
Рис.3.5. а) Правий базис Рис.3.5. б) Лівий базис

Надалі, говорячи про ортонормований базис тривимірного векторного простору, будемо завжди вважати, що базис є правим. Легко переконатися у тому, що базис є ортонормованим тоді й тільки тоді, коли мають місце рівності

. (6.1)

Розглянемо тепер кілька завдань, з якими доводиться часто зустрічатися під час розв’язування практичних і теоретичних питань векторної алгебри.