Тема 3. Елементи векторної алгебри

§ 3.1. Означення вектора

Означення 3.1.1. Як відомо, відрізок прямої задається двома точками – його кінцями, які вважаються рівноправними. Якщо одну із цих точок вважати початковою, а іншу кінцевою, то на відрізку встановлюється напрямок від початку до кінця. Такий відрізок називається спрямованим або вектором. Якщо – початок вектора, а – кінець, то для такого вектора будемо користуватися позначенням . Точка А називається початковою точкою вектора .

Примітка. Оскільки на подальшому у межах курсу поняття вектора буде поступово поширюватися, то означені вище вектори будемо називати геометричними векторами.

Означення 3.1.2. Відстань між кінцем і початком вектора будемо називати довжиною або модулем вектора та позначати одним із символів: або .

Означення 3.1.3. Два або більше векторів називають колінеарними, якщо вони паралельні або лежать на одній прямій.

Означення 3.1.4. Три або більше векторів називають компланарними, якщо всі вони паралельні деякій площини або лежать в одній площині.

Вектор , початок і кінець якого збігаються (довжина вектора при цьому дорівнює нулю) називають нульовим і пишуть . Напрямок нульового вектора вважається невизначеним. Однак за згодою нульовий вектор вважається колінеарним будь-якому ненульовому вектору.

У більшості прикладних задач істотною є довжина вектора та його напрямок. Причому розташування початкової точки вектора у просторі значення не має. Такі вектори називають вільними.

Означення 3.1.5. Два вільних вектори вважаються рівними, якщо вони мають однакові довжини та однакові напрямки.

Невільні вектори діляться на ковзні та зв'язні.

Означення 3.1.6. Два ковзні вектори вважаються рівними, якщо вони мають однакові довжини, їх напрямки збігаються і при цьому вектори розташовані на одній прямій.

Прикладом ковзного вектора є вектор сили в статиці твердого тіла.

Означення 3.1.7. Зв'язні вектори вважаються рівними у тому випадку, коли їхні довжини рівні, напрями збігаються, а також збігаються і точки прикладення.

Вектор швидкості матеріальної точки, що рухається у просторі, є прикладом зв'язного вектора.

Примітка. Надалі будемо розглядати тільки вільні вектори.

§ 3.2. Лінійні операції над векторами

Під лінійними операціями над векторами розуміють операції додавання векторів та множення вектора на число.

Означення 3.2.1. Сумою векторів і називають вектор , який побудовано після виконання послідовності таких дій. З довільної точки простору відкладаємо вектор , з кінця цього вектора відкладаємо вектор . Нехай кінець вектора розташовано у точці С, тоді вектор і є сумою (рис. 3.1).

Рис. 3.1 Сума векторів

Під сумою трьох векторів будемо розуміти вектор . За цим правилом поняття суми легко узагальнюється на випадок будь-якого скінченого числа векторів.

Означення 3.2.2. Вектор будемо називати протилежним вектору , якщо . Вектор, протилежний вектору , будемо позначати: .

Напрямки та протилежні, а модулі однакові. Під різницею векторів і розуміють вектор . Різницю векторів та будемо позначати так: .

Означення 3.2.3. Добутком вектора на число називають вектор, що має довжину , при цьому напрямок вектора збігається з напрямком вектора , якщо , і є протилежним напрямку , якщо . Якщо , то .

Операції додавання векторів та множення їх на числа мають наступні властивості :

1. Додавання векторів комутативне, тобто для будь-яких векторів та : .

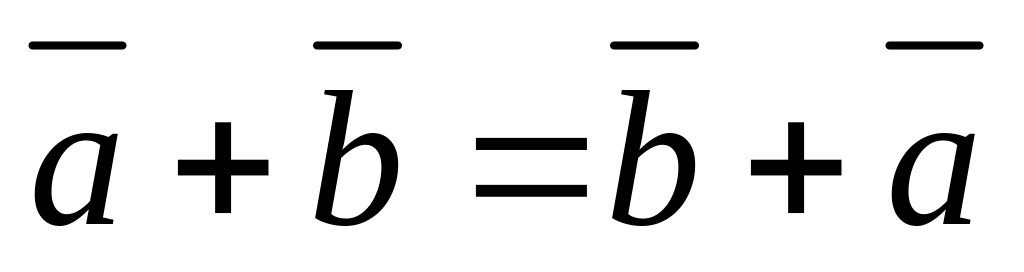2. Додавання векторів асоціативно, тобто для будь-яких векторів , та : .

3. Додавання нульового вектора до будь-якого вектора не змінює останнього: .

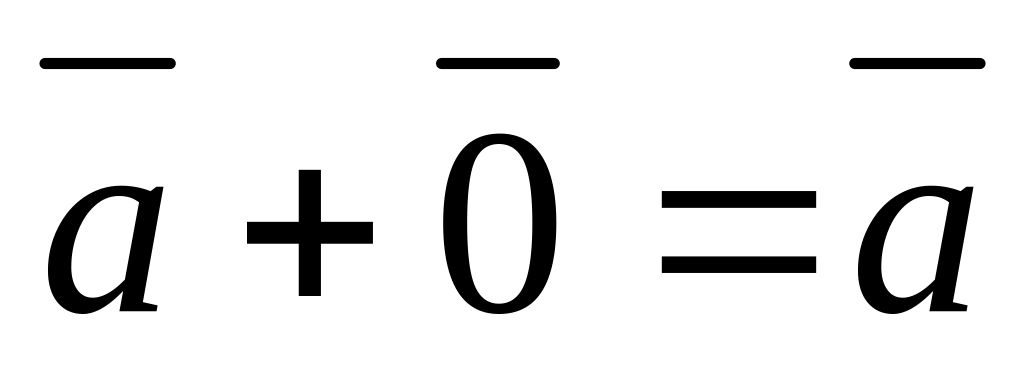4. Для будь-якого вектора : .

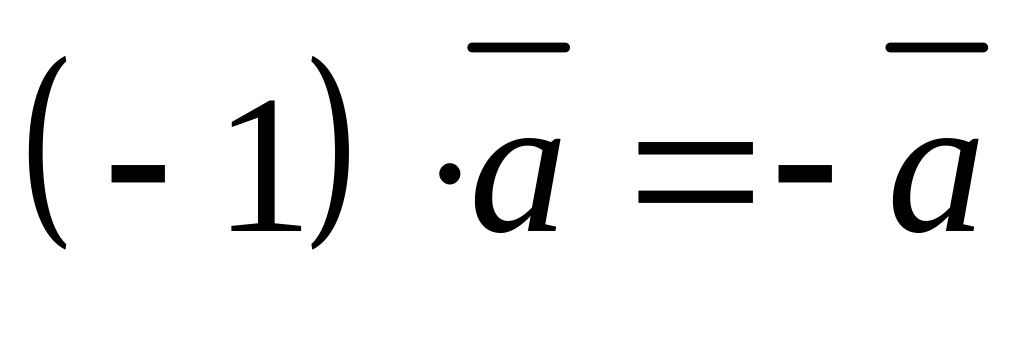5. Множення вектора на число асоціативно, тобто для будь-якого вектора та .

6. Множення вектора на число дистрибутивно відносно операції додавання чисел. Для будь-якого вектора та .

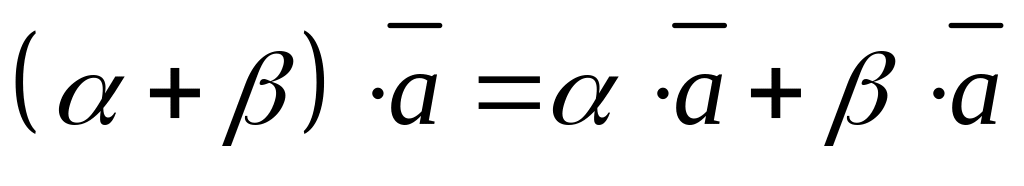7. Множення вектора на число дистрибутивно відносно операції додавання векторів. Для і будь-яких векторів та .

8. Множення вектора на одиницю не змінює останнього: 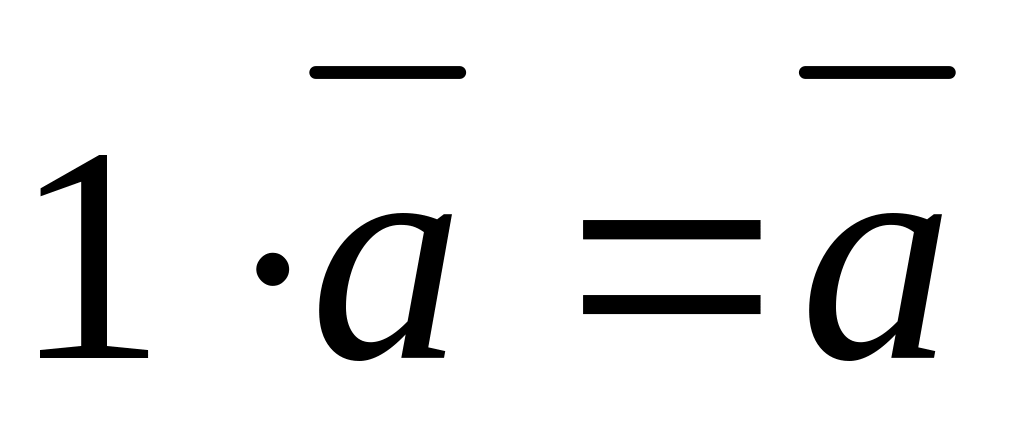, де .

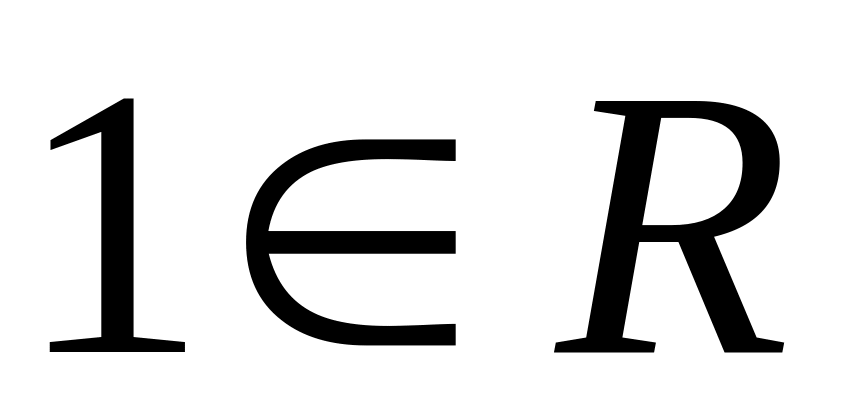Відзначимо, що властивості векторів ідентичні властивостям n-вимірних рядків.

Використовуючи лінійні операції над векторами, можна утворювати суми такого вигляду , які називаються лінійними комбінаціями векторів . Властивості 1-8 лінійних операцій над векторами дозволяють за звичайними правилами розкривати дужки у лінійних комбінаціях, приводити подібні доданки, виносити за дужки загальні множники. У випадку рівності двох лінійних комбінацій можна переносити доданки з однієї частини рівності в іншу, змінюючи їхні знаки на протилежні.

Приклад. Знайти вектори та із системи рівнянь

Розв’язання. Віднімемо від першого рівняння друге, помножене на 2, одержимо . Звідки . Підставимо знайдене у друге рівняння та за звичайними правилами знайдемо .