Лекция 2

Волновое уравнение. Параметры звукового поля. Скорость звука и волновое сопротивление. Спектральные и временные характеристики случайного процесса. Корреляционная и автокорреляционная функции. Сплошные и дискретные спектры, относительная полоса частот, энергетическое суммирование сигналов

Волновое уравнение

Любое нарушение стационарности состояния упругой сплошной твердой, жидкой или газообразной среды в какой-либо точке прост­ранства приводит к появлению возмущений (волн), распростра­няющихся от этой точки.

В твердой среде могут существовать продольные волны, в которых частицы колеблются вдоль распространения вол­ны, и волны поперечные, колебания частиц в которых про­исходят в направлениях, перпендикулярных к распространению волны.

В данном разделе рассматриваются волны в газах и жидкостях, в которых могут распространяться {при отсутствии свободной по­верхности или поверхности раздела двух жидкостей) только про­дольные волны (рисунок 2.1).

Особенности звуковых волн заключаются в том, что частицы в них .колеблются относительно некоторого положения равнове­сия и скорость распространения волны (скорость звука или ско­рость, с которой перемещается максимум давления) значительно больше скорости колебания частиц (колебательной скорости) относительно положения равновесия.

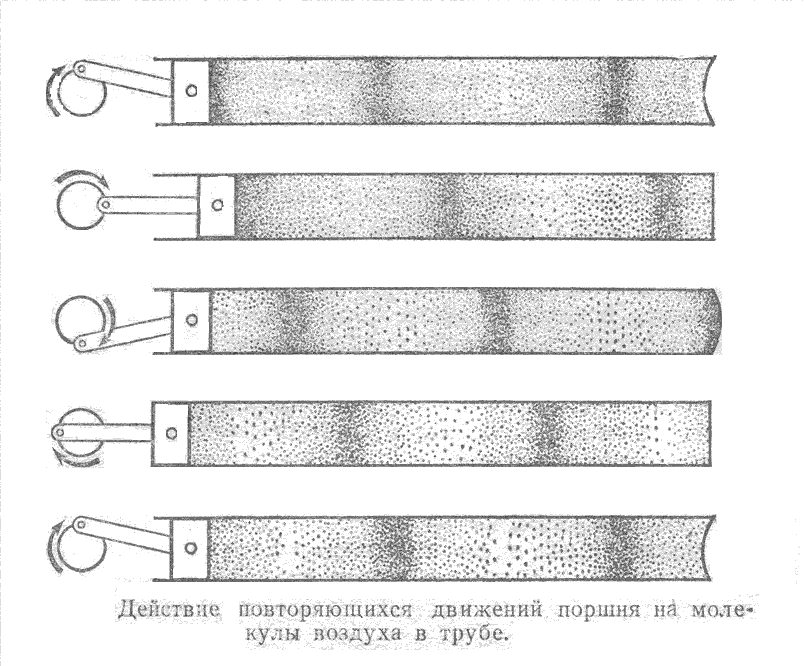
Рисунок 2.1

Рассмотрим физическую интерпретацию волнового уравнения. Для этого рассмотрим трубку с единичным поперечным сечением, наполненную средой с плотностью ρ. Выделим внутри трубки объем, ограниченный двумя плоскостями, расположенными на расстоянии dx друг от друга (рисунок 2.2). Сила, действующая на выделенный элемент в направлении оси Х, равна разности полных давлений, действующих на противоположные стороны элемента, то есть

Р₁ – Р₂ = Р(х) – Р(х + dx) ≈ - (2.1)

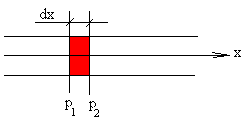
Рисунок 2.2

Если смещение левой грани элемента равно u(x), а правой u(x+dx), то относительная деформация элемента составляет . Сила инерции элемента равна . Приравнивая последнее выражение правой части (2.1), получим:

- (2.2)

Продифференцируем (2.2) по координате Х и воспользуемся законом Гука (давление пропорционально степени сжатия) , где β – сжимаемость среды (обратная величина модуля упругости 1/К). Учитывая , что , где р – мгновенное значение отклонения давления в звуковой волне от равновесного его значения Р₀, получим

; .

Мы получили волновое уравнение для одномерного случая. Первый член волнового уравнения обусловлен сжатием элемента среды, а второй – инерцией. В трехмерном случае звуковое давление в жидкости удовлетворяет следующему волновому уравнению:

, (2.3)

где - оператор Лапласа, с – скорость звука в среде. Связь между вектором колебательной скорости и звуковым давлением в среде определяется уравнением Эйлера

, (2.4)

где .

Можно считать, что градиент температуры в волне, обуслов­ленный сжатием среды, в диапазоне частот звуковых волн, встре­чающихся в практике борьбы с шумом, так мал, что явления теплообмена между соседними частицами не имеют места, и ко­лебательный процесс является адиабатическим. Тогда скорость звука

,

где χ = Ср/С_V - показатель адиабаты (для воздуха χ = 1,41); Ср —теплоемкость воздуха при постоянном давлении; С_V - теплоемкость при постоянном объеме; ρ₀ - плотность (масса единицы объема) покоящейся среды.

Изменение давления и изменение плотности, отсчитанные от равновесных значений Р₀ и ρ₀, в звуковой волне связаны соотно­шением .

Звуковое поле является векторным полем, поскольку движение каждой частицы описывается вектором колебательной скорости с компонентами v_x, v_y, v_z. В идеальной жидкости при отсутствии вязкости равнодействующая сил, действующих на элемент среды, проходит через его центр и вращательный момент равен 0, то есть выполняется условие . В этом случае звуковое поле является незавихренным и его можно охарактеризовать исчерпывающим образом одной скалярной функцией - потенциалом скорости φ (х, y, z, t). По известному потенциалу скорости можно определить звуковое давление и колебательную скорость. Колебательная скорость равна

, (2.5)

а, воспользовавшись уравнением Эйлера (2.4), получим:

. (2.6)

Наряду с волновым уравнением (2.3) в акустике для описания волновых процессов широко используется уравнение Гельмгольца, которое получается при подстановке в уравнение (2.3) звукового давления в комплексном виде , где - амплитуда колебания, ω – угловая частота:

(2.7)

В уравнении Гельмгольца (2.7) физический смысл имеет лишь вещественная часть давления.

В математической физике волновое уравнение относится к уравнениям гиперболического типа (члены уравнения имеют разные знаки), а уравнение Гельмгольца – к уравнениям эллиптического типа (все члены уравнения имеют одинаковый знак). Методы решения этих уравнений существенно различаются.

Физическое различие между гиперболическими и эллиптическими уравнениями хорошо иллюстрируется на примере акустики движущейся среды. Уравнение Блохинцева, описывающее распространение звука в среде, движущейся в направлении оси Х со скоростью u=Mc, где М – число Маха, имеет вид:

.

Если М<1, то уравнение является эллиптическим и звуковые поля в среде, движущейся с дозвуковой скоростью, не отличаются качественно от полей в неподвижной среде. Если же M>1, то уравнение становится гиперболическим. Решения таких уравнений рассматриваются в газодинамике больших скоростей, когда в поле течения появляются скачки уплотнения и ударные волны, в частности, при исследовании распространения звукового удара от сверхзвукового самолета.

Звуковая волна. Параметры звукового поля.

Волна называется бегущей, если обратная волна отсутствует. Пример распространения плоской бегущей волны представлен на рисунке 2.1 Стоячей называется волна, если она образована наложением двух одинаковых волн — прямой .и обратной, движущихся в про­тивоположных направлениях. Отношение звукового давления к колебательной скорости в плоской бегущей волне не зависит от амплитуды колебаний и называется волновым сопротивлением среды:

(2.8)

В техниче­ской системе единиц при нормальных атмосферных условиях (t = 20° С, Р₀= 10 330 кГ/м²) волновое сопротивление W₀ = = 42 кГ сек/м³, в системе СИ W₀ = 420 н сек/м². В бегущей вол­не скорость и давление отличаются лишь масштабом - увеличе­нию давления соответствует увеличение колебательной скорости, и наоборот, скоростям частиц в отрицательном направлении соответствуют разрежения.

Изменение плотности в бегущей волне равно:

(2.9)

Бегущая волна переносит энергию в направлении своего дви­жения. Средний поток энергии в какой-либо точке среды в единицу времени, отнесенный к единице поверхности, нормальной к .на­правлению распространения звука, называется интенсивностью звука в данной точке:

I = lim 1/T , (2.10)

где черта означает осреднение во времени t; V ~ колебательная скорость частиц в звуковой волне. Интенсивность измеряется либо в кГм/см² или кГ/с м, либо в системе СИ в вт!м².

Интенсивность звуков, с которыми приходится иметь дело в практике борьбы с шумами, изменяется в очень широких пре­делах. Поэтому введена логарифмическая величина - уровень интенсивности звука

L_i = 10lg , дБ (2.11)

Где I₀ = 10^-12 вт/м² = 10^-13 кГм/см² называется пороговой. В практике борьбы с современными шу­мами приходится иметь дело с уровнями интенсивности, лежа­щими в диапазоне от 20 до 170 дБ (т. е. диапазон изменения ин­тенсивности составляет 10¹⁵).

Человеческое ухо и многие акустические приборы чувстви­тельны не к интенсивности, а к среднему квадрату звукового давления. Поэтому введена величина уровня звукового давления

L_р = 10 lg = 20 lg , дБ (2.12)

где пороговое звуковое давление р₀ выбрано таким образом, что при нормальных атмосферных условиях

I₀ = (2.13)

где и c₀ — плотность и скорость звука при нормальных ат­мосферных условиях. Тогда

p₀ = 2 10^-4дин/см² = 2 10^-5 н/м² = 2 10^-4 кГ/м²

Связь между уровнем интенсивности и уровнем звукового давления можно получить, разделив уравнение (2.10) на (2.13):

=

Прологарифмировав последнее соотношение, получим соотношение между уровнем интенсивности и уровнем звукового давления:

(2.15)

При нормальных атмосферных условиях L_j = L_р.

В таблице рассмотрено соотношение между интенсивностью звука, величиной звукового давления и уровня звукового давления.

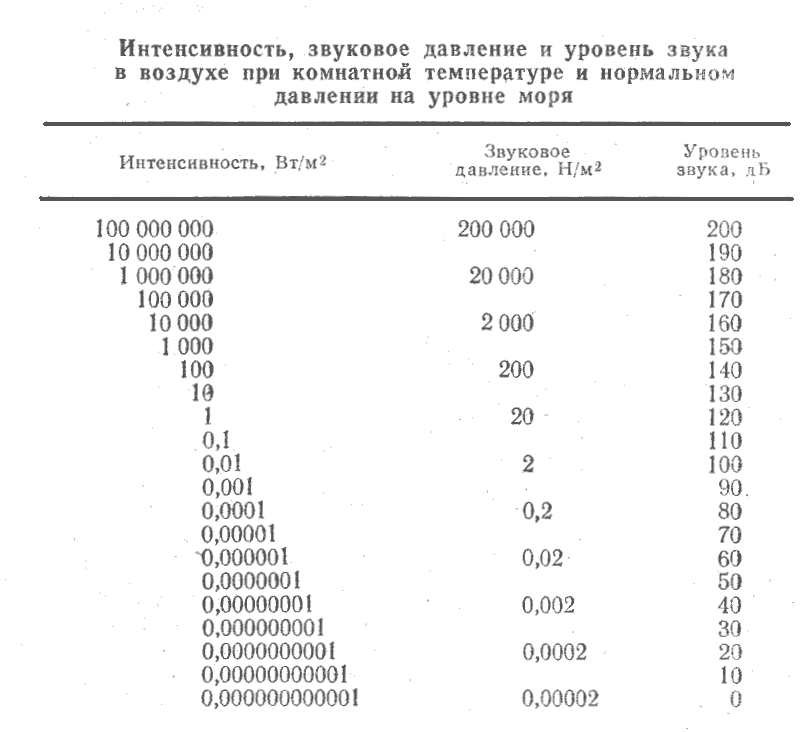
В простейшем случае физические параметры в звуковой вол­не меняются по закону косинуса (или синуса)

(2.16)

где р_m- амплитуда (р здесь не только звуковое давление, но и плотность, колебательная скорость, потенциал); ω—круговая частота; t - время. Такой звук называется чистым тоном.

Круговая частота связана с обычной частотой f , то есть с. числом полных колебаний в сек, измеряемым в герцах (гц] соотноше­нием

(2.17)

Как известно, в комплексных величинах

.

Обозначив , где к — волновое число; λ = с / f - длина звуковой волны, то есть расстояние между сосед­ними максимумами звукового давления, и применив комплексные обозначения, получим уравнение рас­пространения прямой плоской волны в комплексной форме:

, (2.18)

где - мнимая единица. Действительная часть выражения (2.18) соответствует выра­жению (2.16). Вместо (2.18) можно написать

.

Выражения е^iωt и е^-ikx называются соответственно времен­ным и фазовым множителями. Физические характеристики синусоидальных звуковых волн выражаются с помощью следующих соотношений.

Звуковое давление:

;

; (2.19)

.

Колебательная скорость:

;

; (2.20)

Интенсивность звука:

(2.21)

Пример. Определить физические характеристики бегущей плоской синусо­идальной волны, соответствующей звуку с уровнем интенсивности L_i = 160 дБ при нормальных атмосферных условиях.

дБ, откуда кГм/с∙м².

Амплитуда звукового давления (2.19): кГ/м²;

Амплитуда колебательной скорости (2.20): ; м/с

Относительная ампли­туда изменения плотности .

На примере видно, что даже при очень высоких уровнях ин­тенсивности колебательные скорости малы по сравнению со ско­ростью звука, звуковые давления малы по сравнению с атмос­ферным давлением, а изменения плотности в волне очень неве­лики по сравнению с плотностью атмосферы.

Плотность звуковой энергии Е определяется количеством энергии в единице объема. В технической системе единиц размерность [Е] обозначается кГм/м³ или кГ/м², в СИ - дж/м³.

Скорость переноса энергии звуковой волны в неподвижной атмосфере равна скорости распространения звука с. Интенсив­ность звука в плоской бегущей волне можно представить как произведение плотности энергии Е на скорость ее переноса с: I = Еc, откуда

(2.22)

Плотность звуковой энергии есть величина скалярная; она лучше характеризует энергию поля, чем интенсивность в тех слу­чаях, когда направление звука является неопределенным, напри­мер, в закрытых помещениях.

Звуковая волна при распространении переносит не только энергию, но и импульс. Другими словами, она оказывает давле­ние на предметы, находящиеся в звуковом поле. Это давление радиации обычно весьма невелико, но при высоких интенсивностях может стать заметным.

Наличие давления радиации исполь­зуется для измерения интенсивности в сильных звуковых полях. Оно представляет собой эффект второго порядка малости по от­ношению к звуковому давлению и обусловлено преимущественно наличием квадратов скоростей в уравнениях движения, отбрасы­ваемых при выводе уравнения акустики.

Величину давления радиации впервые определил Релей. Она зависит от поглощающих свойств площадки, на которую падает звуковой луч, от ориентировки этой площадки и ее размеров. В очень важном случае нормального падения плоской волны на твердую непоглощающую стенку бесконечных размеров давле­ние радиации равно:

(2.23)

Спектральные и временные характеристики

Отклонение физической величины р(t) в звуковой волне от состояния покоя может быть определено для каждого момента времени (детерминированный процесс) и носить случайный не­определенный характер (случайный процесс). Примером процес­са первого рода является шум вращения воздушного винта, звук сирены; примером процесса второго рода - шум воздушной струи. Совокупность детерминированных процессов может носить характер случайного процесса (рисунок 2.3), например наложение детермини­рованных шумов выхлопа отдельных автомобилей дает уличный шум, имеющий случайный характер.

Периодические процессы, повторяющиеся через время Т, на­зываемое периодом, являются детерминированными. Кратковре­менные процессы всегда являются непериодическими.

Случайный процесс можно представить состоящим из боль­шого числа кратковременных непериодических процессов, отли­чающихся друг от друга. Случайный процесс, средние статисти­ческие характеристики которого со временем не меняются, назы­вается стационарным, хотя он состоит из неповторяющихся эле­ментов.

Раньше шумом называли всякий звук случайного характера. В соответствии с установившейся в настоящее время терминоло­гией шумом будем называть всякий нежелательный звук в слышимом диапазоне частот. Поэ­тому при рассмотрении физических характеристик поля на практике чаще используется термин «звук », а при описании источников звука или физиологического воздействия звукового поля на че­ловека преимущественно применяется термин «шум».

Рисунок 2.3

Спектр периодического процесса

В силу линейности уравнений акустики сложное колебание р(t) всегда можно представить в виде суммы (суперпози­ции) более простых колебаний, например в виде суммы синусои­дальных волн. Для периодического детерминированного процес­са в какой-либо точке среды эта сумма будет иметь вид:

(2.24)

где n - целые числа, а основная круговая частота ω связана с периодом Т соотношением .

Величины С _n являются комплексными амплитудами отдель­ных синусоидальных составляющих. Они выражаются формулой

(2.25)

Процесс определения амплитуды С_п называется гармониче­ским анализом функции р(t), а величины С_п называются гармониками периодического процесса. Если учесть комплексность величины С_п, то выражение (2.24) мож­но представить в виде:

Величина А₀ является постоянной слагающей; если рассмат­риваются отклонения физических величин в волне от невозму­щенного состояния, то А₀ = 0. Аргумент называется фазой колебания, ψ_n - начальной фазой. Максимальное откло­нение р_тп называется амплитудой. Индекс п называется но­мером гармоники; значению п=1 соответствует первая гармони­ка или основная частота. Колебания с кратными друг другу ча­стотами называются гармоническими составляющими.

Зависимость амплитуд р_тп или фаз ψ_n от частоты колебаний называется соответственно спектром амплитуд или фаз. Обычно в практике борьбы с шумом интерес представляет лишь абсолютная величина (модуль) гармоник р_тп безотноси­тельно к фазе ψ_n.

Средний квадрат периодической функции р(t), исходя из определения средней величины, равен:

(2.26)

Проделав необходимые вычисления, получим для синусои­дальных составляющих

. (2.27)

Это важная формула, так как она устанавливает связь мощности процесса (например, интенсивность звука в данной точке звукового поля) с амплитудами синусоидальных составляющих. Каждая величина пропорциональна мощности синусоидальной составляющей с амплитудой Р_mn. Таким образом, мощность периодического процесса равна сумме мощностей гармоник (энергетическое суммирование со­ставляющих). Начальные фазы гармоник никакой роли при этом не играют.

Зависимость от частоты называется спектром мощности или энергетическим спектром данного процесса.

Среднее квадратическое значение физической величины называется действующим или эффективным ее значением. Действующие значения гармоник выражаются через действую­щие значения амплитуд как .

Процесс может состоять из некратных друг другу синусои­дальных колебаний (почти периодический процесс, не являю­щийся периодическим), например сложение двух процессов с не­кратными друг другу периодами Т₁ и Т₂. В этом случае формула (2.27) также справедлива. Таким образом, средняя мощность любого детерминированно­го периодического или почти периодического процесса равна сум­ме мощностей его составляющих.

Спектр случайного процесса

Случайный процесс (каковыми в большинстве случаев явля­ются шумы) не имеет резко выраженного периода и поэтому, в отличие от периодического процесса, не может быть выражен че­рез гармонические составляющие. Однако он также обладает важными спектральными харак­теристиками.

Рассмотрим характеристику стационарного случайного шума. Установив­шимся во времени устойчивым процессам соответствуют обычно такие шумы, вероятностные характеристики которых не изменя­ются при любом сдвиге по времени. Если в бесконечной записи случайного процесса выделить несколько произвольных участ­ков одинаковой продолжительности Т (такие участки называются реализациями данного случайного процесса) и наложить друг на друга, то записанные кривые не совпадут ни при каких Т.

Такой непрерывный процесс обладает средней мощностью и энергетическим спектром этой мощности, т. е. распределением ее по частотам колебаний. Средняя фаза в силу случайности ко­лебания смысла не имеет.

Мощность такого процесса

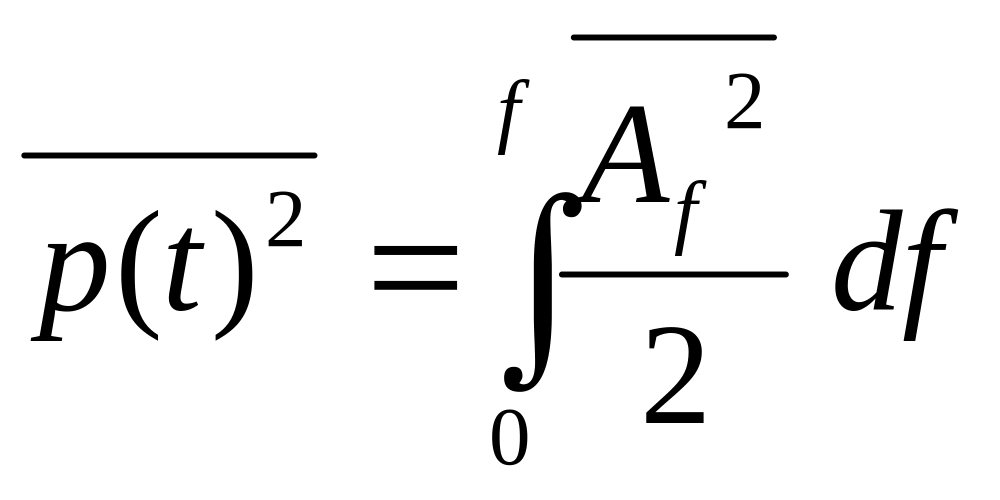(2.28)

где - средняя по времени мощность, приходящаяся на по­лосу частот шириной 1 гц.

Зависимость - от частоты называется энергетическим спект­ром данного случайного процесса или спектром его мощности. Величину можно назвать эффективной амплитудой слу­чайного процесса на частоте f, отнесенной к полосе шириной 1 гц.

Вид спектра зависит от спектральных характеристик одиноч­ных процессов, совокупность которых составляет случайный про­цесс, и от распределения их во времени.

Таким образом, средняя мощность периодического, почти пе­риодического и случайного процессов равна сумме мощностей их синусоидальных составляющих.

Совсем другая .картина может наблюдаться, если складыва­ются колебания от двух различных источников

P(t) = P₁(t) + P₂(t),

а не спектральные составляющие одного и того же .процесса. В этом случае:

(2.29)

Процессы p₁ и р₂ называются некогерентными в том случае, если их взаимная мощность 2р₁р₂ равна нулю. Для независимых друг от друга процессов, как показывает теория вероятностей, это условие соблюдается всегда.

Степень причинной связи двух одновременных процессов характеризуется их моментом (функцией) корре­ляции

, (2.30)

или нормированной величиной, называемой коэффициентом корреляции:

(2.31)

Условие равенства нулю коэффициента корреляции не всегда означает отсутствие причинной связи между составляющими, как .мы видели на примере синусоидальных составляющих одно­го и того же процесса.

При сложении двух процессов с одной и той же частотой они могут быть как когерентными, так и некоге­рентными (в зависимости от разности фаз составляющих).

Степень причинной связи во времени одного и того же слу­чайного процесса характеризует функция автокорреляции

(2.32)

где τ — время задержки. Для стационарного слу­чайного процесса R(τ) не зависит от момента време­ни, принятого за нуль.

Функция автокорреля­ции случайного процесса однозначно связана с его спектром мощности. Функ­ция автокорреляции и спектр мощности полностью равноправны при описании случайного процесса.

Составляющие энергети­ческого спектра стационар­ного случайного процесса сами являются случайными функциями времени, и их можно считать постоянными лишь при бесконечном времени усреднения. Реальные измерительные приборы обладают конечным временем усреднения, и поэтому показания их при измерениях спектра испытывают флуктуации случайного характера, размах которых зависит от свойств при­бора и ширины полосы частот. Чем эта полоса 'больше, тем флуктуации меньше.

По этой же причине при сложении случайных звуков, а так­же периодических сигналов, отличающихся по частоте менее чем на 10 гц, слух человека различает биения, так как время осред­нения человеческого уха составляет конечную величину порядка 1 00 мсек.

Графическоео изображение спектров.

Спектр периодического .процесса с основной частотой f₁ изобра­жается , в виде зависимости амплитуд составляющих от частоты (рисунок 2.4а). На графике откладываются отрезки, пропорциональные

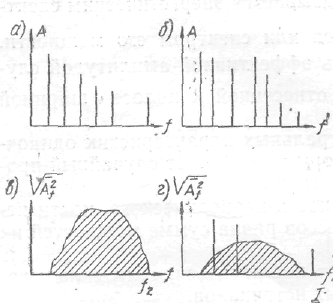
Рисунок 2.4

либо амплитудам, либо их квадратам. Начальные фазы нас не интересуют.

Спектр почти периодического процесса имеет такой же вид, только частоты не всех составляющих кратны друг другу {рисунок 2.4б). Спектры процессов, составленных из синусоид, называются дискретными или линейчатыми. Следует обратить внимание на то, что линии на таком спектре, теоретически рассуждая, не име­ют ширины.

Спектр случайного или непериодического процесса (рисунок 2.4в) является оплошным, и поэтому его изображение требует обязательной оговорки о ширине ∆f элементарных полосок, к которым оно относится. По оси ординат откладываются, как по­казано на рисунке, либо средние квадратические значения эф­фективных амплитуд , либо соответствующие значения средних квадратов (энергий) в указанной полосе частот

, либо действующее значение амплитуды , либо уровни этих величин в дБ. Частота f₁ называется .нижней граничной частотой полосы спектра, а f₂ — верхней. За среднюю частоту полосы обычно при­нимают среднюю геометрическую, равную

(2.33)

При оперировании с шумами их частотные .составляющие поч­ти всегда считают некогерентными, и предполагают, что они подчиняются энергетическим соотношениям. Тогда, если известна эффективная амплитуда полосы ∆₂ = f₂-f₁, то амплитуду полоски ∆₁f = 1 гц легко рассчитать по формуле

(2.34)

Обратный пересчет будет справедлив, если известно, что в диапазоне f₂-f₁ амплитуда существенно не изменяется.

Спектр нескольких пе­риодических и случайных процессов имеет смешанный характер (рисунок 2.4г) и изображается в виде наложения сплошного и дискретного спектров, причем совмещение их на одном графике является условным, так как амплитуда дискрет­ной составляющей не зависит от ширины полосы спектра, а ор­дината сплошной части от этой ширины сильно зависит в соот­ветствии с (2.34). Недопустимо распределять мощность дискрет­ной составляющей по частотам в полосе, так как это не соответ­ствует физической природе процесса.

Полосы частот.

При исследованиях шумов часто пользуются анализаторами с постоянной относительной полосой пропускания f₂/f₁=const. Полоса, у которой отношение f₂/f₁ ⁼ 2, называется октавой; если

f ₂/f₁ =1.26, то ширина полосы равна '/з октавы. При измерениях шумов используются также анализаторы с постоянной абсолютной полосой пропускания ∆_f = const. Стандарт­ные полосы указаны в таблице.

Октавные полосы частот			Третьоктавные полосы частот
Граничные частоты, Гц	Среднегеометрические частоты, Гц	Граничные частоты, Гц		Среднегеометрические частоты, Гц
45-90	63	45-55 55-70 70-90		50 63 80
90-180	125	90-113 113-141 141-181		100 125 160
180-355	250	181-226 226-282 282-356		200 250 315
355-710	500	356-450 450-565 565-710		400 500 630
710-1400	1000	710-900 900-1130 1130-1415		800 1000 1250
1400-2800	2000	1415-1800 1800-2260 2260-2820		1600 2000 2500
2800-5600	4000	2820-3560 3560-4500 4500-5650		3150 4000 5000
5600-11200	8000	5650-7100 7100-9000 9000-11300		6300 8000 10000
11200-22400	16000	11300-14100 14100-18100 18100-22000		12500 16000 20000

Уровень звукового давления

При анализе шума в качестве основной физиче­ской характеристики процесса обычно .выбирают уровень звуко­вого давления. Уровень в полосе ∆f = 1 Гц называется уровнем спектра и обозначается β_Ш. Исходя из условия некогерентности составляющих связь между уровнем в полосе частот f₂ –f₁ и уровнем спектра записывается в виде:

L_(f2-f1) = 10lg (2.35)

Эта формула следует из закона сложения составляющих:

(2.36)

и из формулы (2.12), которую можно переписать в виде:

(2.37)

Таким образом, для конечного числа составляющих суммарный уровень звукового давления равен:

, (2.38)

где n — число полос сплошного шума плюс число дискретных составляющих, или

10^L/10 = (2.39)

Если имеется п одинаковых составляющих с уровнем звуко­вого давления каждой L_i , то суммарный уровень звукового давления будет равен:

L = L_i + 10lg n (2.40)

Чтобы облегчить вычисление суммарного уровня звукового давления при сложении “n” уровней, можно вместо формулы (2.38) воспользо­ваться графиком (рисунок 2.4), построенным последующему соотношению:

.

Рисунок 2.4

По оси абсцисс отсчитывается разность L₁-L₂ , по оси орди­нат - величина ∆L, которую нужно прибавить к большему уровню L₁, чтобы получить суммарный уровень. Так последова­тельно складываются все п составляющих.

Этим же графиком удобно пользоваться при определении уровня звукового давления, развиваемого несколькими некоге­рентными источниками.

Пример. Определить суммарный уровень звукового давления трех ком­понентов, уровни каждого из которых равны L₁=75 дБ, L₂=62 дБ и L₃=59 дБ.

Вычисляем значение L₂ -L₃=3 дБ; по графику находим ∆L=1,8 дБ, от­куда L₂^”= 62+1,8=63,8 дБ; L₁ – L₂^” =11.2 дБ; ∆L=0,3дБ; L = 75+0,3= =75,3 дБ.

Спектры, выраженные в уровнях звукового давления, обычно вычерчиваются в полулогарифмических координатах — равно­мерная шкала уровней и логарифмическая шкала частот.