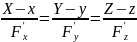Кручение пространственной кривой

Кривизна характеризует отклонение кривой от криволинейной формы, а кручение (2-я кривизна) – отклонение кривой от плоской формы

b

b

M

ψ

P₀

Пусть т. и М – т. близкая к т. . Обозначим - угол между соприкасающимися плоскостями в этих точках (или угол между бинормалями).

Тогда под абсолютным кручением кривой в т. будем понимать:

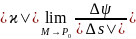
Кручение

Теорема. Регулярная (трижды непрерывно дифференцируемая) кривая в каждой своей точке, где кривизна отлична от нуля, имеет определение абсолютное кручение 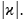Если 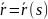естественная параметризация кривой, то

□ Если кривизна в т. отлична от нуля, то она отлична от нуля в окрестности т. вектора - не коллинеарны в любой т. М близкой к существует единственная соприкасающаяся плоскость

b(s+

b(s)

M

b(s+

P₀

ψ

b(s)

b(s+

ψ

b(s)

n

Получим, что .

Но 1) 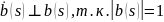(свойство векторной функции).

2)

Из 1) и 2) следует, что

Известно, что

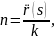
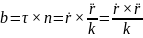, тогда .

Получаем:

О знаке кручения (определение кручения)

Из параллельности векторов и следует, что при движении по кривой в сторону возрастающих s соприкасающаяся плоскость кривой поворачивается около касательной (кручение, длина вектора выражает скорость вращения вектора бинормали, а следовательно соприкасающейся плоскости).

Кручение кривой определяется равенством Знак «+» берется, если вращение соприкасающейся плоскости происходит в направлении от b к и « », если вращение происходит в направлении от . Таким образом, .

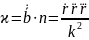Замечание. Точки кривой, в которых кручение равно нулю, называются точками уплощения.

Вычисление кручения

1) Кривая r = r(t) задана в естественной параметризации.

,

1) Так как

2)

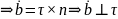
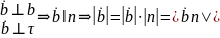
Но вектор кривизны.

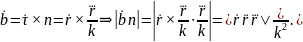
О знаке. Т.к. при движении вдоль кривой в сторону возрастания параметра s соприкасающаяся плоскость поворачивается возле касательной. Если движение происходит от от b к , то «+» и если от , то « ».

2) Кривая r = r(t) задана векторно-параметрически:

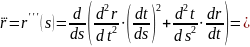
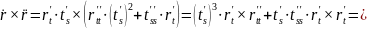
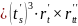
3) Кривая задана параметрически:

4) Кривая задана явно:

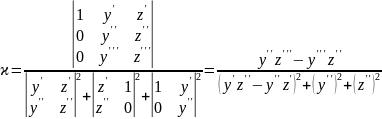
Формулы Френе-Серре

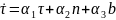
b

n

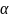
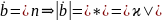
Натуральные уравнения пространственной кривой

M

O

Пусть на данной кривой L выбрана т. …. О и установим положительное направление для дуг, тогда положение любой точки М на L определяется заданием длины дуги ОМ. Кривизна и кручение т. М тоже будут зависеть от длины дуги, т.е.

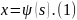
Определение. Уравнения (1) выражающие кривизну и кручение кривой через её дугу, называются «натуральными» или «внутренними» уравнениями этой кривой.

Теорема. Каковы бы ни были непрерывные функции существует одна и только одна линия (с точностью до положения в пространстве), натуральные уравнения которой есть: .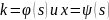

Геометрия поверхностей

1) Понятие поверхности. Определение поверхности.

Def. Под элементарной поверхностью (простой поверхностью) понимают любые семейства точек, которые можно топологично отобразить на замкнутый круг.

Замечание. Локально (в малом) поверхность получается в результате непрерывной деформации в 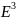(гомоморфизм) плоской области.

Глобально (в целом) поверхность «склеивается» из таких кусков.

Def. Поверхностью называют множество точек, состоящих из конечного или счетного множества простых поверхностей склеенных друг с другом.

Будем рассматривать поверхности, которые гомоморфны некоторой плоской области D. Область D – область плоскости переменных u и v.

Замечание. Гомоморфизм же области D в пространстве , в результате которого и возникает рассматриваемая поверхность, обычно задают, выбрав … - т. О и вектор-функцию .

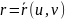2) Способы задания поверхности:

O

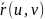
а) векторно-параметрический: r = r(u,v).

б) если в введена прямоугольная система координат:

r(u,v) = х(u,v)i + y(u,v)j + z(u,v)k

в) в частном случае, когда из уравнений 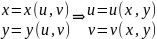и подставим в явное уравнение поверхности

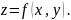
г) неявное задание поверхности:

Замечание. Мы будем изучать регулярные или дифференцируемые поверхности.

Def. Поверхность является - гладкой (регулярной) поверхностью, если среди её параметризации найдется такая параметризация r = r(u,v), что вектор-функция r(u,v) – n раз непрерывно диффенцируема и в каждой точке (u,v) её первые частные производные 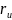(u,v) и (u,v) неколлинеарны.

3) Кривые на поверхности. Координатные линии.

Рассмотрим в пространстве поверхность Ф заданную гладкой параметризацией r = r(u,v). Вектор-функция r(u,v) определена в области D переменных u и v.

Если в области D выбрать кривую , то её образом будет кривая на поверхности Ф. Кривую в D можно задать параметрически: тогда

Замечание 1. Уравнения называются внутренними уравнениями кривой на поверхности Ф.

Замечание 2. Если в качестве внутренних уравнений взять семейства кривых:

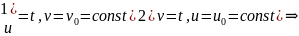
координатная сеть на множестве D, то они определяют координатные линии на поверхности Ф.

4) Касательная плоскость к поверхности Ф.

Def. Под касательной плоскостью к любой поверхности в данной точке будем понимать плоскость, которая содержит все касательные прямые к кривым, лежащим на поверхности и проходящим через выбранную точку. Это определение подтверждает следующее:

Теорема. Пусть Ф – гладкая поверхность, вектор-функция r(u,v) определенная на D её гладкая параметризация. Точка плоскость, проходящая через т. х и имеющие векторы своими направляющими векторами. Тогда все касательные прямые в т. х к гладким кривым, лежащим на поверхности Ф и проходящим через т. х, содержаться в плоскости и заполняют

Из теоремы следует, что векторы R – r, компланарные векторное уравнение касательной плоскости или через координаты:

=0.

В случае явного задания поверхности:

=0 или

В случае неявного задания поверхности:

5) Нормаль к поверхности и её уравнение.

Определение. Прямая, проведенная через заданную точку поверхности и ортогональная касательной плоскости поверхности проведенной через эту же точку поверхности, называется нормалью к поверхности в данной точке.

Замечание. Иногда называют вектор касательной плоскости в данной точке.

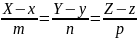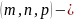Уравнение нормали: , где координаты вектора

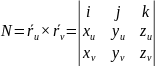
В этом случае: а) для явного задания поверхности:

б) для неявного: