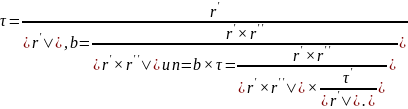- •Параметризация кривой
- •Касательная к кривой (в частности плоской)
- •Нормаль к кривой
- •Подкасательная и поднормаль
- •Длина дуги
- •Плоская кривая
- •Е стественная параметризация кривой
- •Кривизна кривой
- •Радиус кривизны кривой. Центр кривизны кривой. Круг кривизны кривой (для плоской кривой)
- •Радиус и центр кривизны кривой
- •Геометрия пространственных кривых
- •С b опровождающий трехгранник. Формулы Френе. Кручение
- •Главная нормаль. Бинормаль и её уравнение. Спрямляющая плоскость
- •Кручение пространственной кривой
- •Формулы Френе-Серре
- •Натуральные уравнения пространственной кривой
- •Геометрия поверхностей
- •О внутренней геометрии поверхности.
- •Первая квадратичная форма поверхности (метрика поверхности).
С b опровождающий трехгранник. Формулы Френе. Кручение
n
2. Уравнение нормальной плоскости
b
R(t)
R(t)
R(t)
норм
n
r(t)
Def. Множество всех нормалей проведенных к пространственной кривой в рассматриваемой точке и образуют нормальную плоскость.
Замечание. В качестве вектора нормали выбирают вектор касательной кривой, т.е. вектор , тогда:

 -
уравнение нормальной плоскости
-
уравнение нормальной плоскости
Если
кривая задана неявно (как пересечение
поверхностей
 и
и
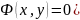 ,
то вектор
,
то вектор
 и
и
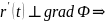 вектора
вектора
 - компланарные
- компланарные
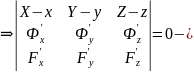 уравнение
нормальной плоскости.
уравнение
нормальной плоскости.
3. Соприкасающаяся плоскость криво
ℒ

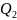
Пусть
т.
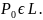 возьмем на ней еще точки
возьмем на ней еще точки
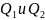 расположенные по разные стороны от т.
расположенные по разные стороны от т.
 проведем через них плоскость.
проведем через них плоскость.
Def.
Предельное положение построенной
плоскости, проходящей через т.
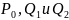 когда
две из них
стремятся к третьей т.
,
и будем называть соприкасающейся
плоскостью кривой в т.
когда
две из них
стремятся к третьей т.
,
и будем называть соприкасающейся
плоскостью кривой в т.
Теорема.
Пусть r
= r(t)
– дважды непрерывно дифференцируемая
кривая. Если в т.
вектора
 - неколлинеарны (
),
то в этой точке существует соприкасающаяся
плоскость, и она проходит через вектора
- неколлинеарны (
),
то в этой точке существует соприкасающаяся
плоскость, и она проходит через вектора
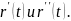
Замечание 1. Точки кривой, в которых векторы - коллинеарны, называются точками распрямления кривой.
Замечание 2. Вектор нормали, лежащий в соприкасающейся плоскости, называется главным вектором нормали кривой. Орт этого вектора
 .
.
Замечание
3.
Из теоремы следует, что вектора
 - коллинеарные, поэтому
- коллинеарные, поэтому
1)
 или
или
 векторное уравнение плоскости или
векторное уравнение плоскости или
2)
 уравнение соприкасаящейся плоскости
в координатном виде.
уравнение соприкасаящейся плоскости
в координатном виде.
Так
как
 принадлежат
соприкасающейся плоскости , то
соприкасающуюся плоскость назавают
плоскостью ускорения:
принадлежат
соприкасающейся плоскости , то
соприкасающуюся плоскость назавают
плоскостью ускорения:
а)
вектора
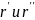 принадлежат соприкасающейся плоскости,
т.к. плоскость проходит через касательную
прямую;
принадлежат соприкасающейся плоскости,
т.к. плоскость проходит через касательную
прямую;
б)
 принадлежит соприкасающейся плоскости,
т.е. плоскость проходит через главный
вектор нормали;
принадлежит соприкасающейся плоскости,
т.е. плоскость проходит через главный
вектор нормали;
в)
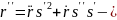 т.е. по нормале разложения вектора
т.е. по нормале разложения вектора
 лежат в одной плоскости.
лежат в одной плоскости.
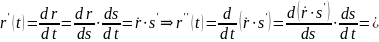

Главная нормаль. Бинормаль и её уравнение. Спрямляющая плоскость
Def 1. Плоскость, проходящая через касательную к кривой в т. и ортогональная соприкасающейся плоскости, называется спрямляющей плоскостью.
Def 2. Бинормалью называется прямая, которая получается при пересечении спрямляющей плоскости нормальной плоскостью.
З
амечание.
Из определений следует, что вектор
бинормали
 - ортогонален касательному вектору
(т.к. спрямляющая плоскость перпендикулярна
касательной) и вектору главной нормали
( т.к. вектор главной нормали принадлежит
соприкасающейся плоскости), т.е.
- ортогонален касательному вектору
(т.к. спрямляющая плоскость перпендикулярна
касательной) и вектору главной нормали
( т.к. вектор главной нормали принадлежит
соприкасающейся плоскости), т.е.

У
B
равнение бинормали
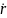

r
R
Вектор
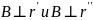 (т.к. в
(т.к. в
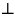 соприкасающейся плоскости)
соприкасающейся плоскости)

Теперь можем записать уравнение бинормали в каноническом виде:

или

Уравнение главной нормали
В
качестве направляющего вектора главной
нормали можно выбрать вектор равный
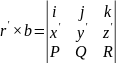 ,
тогда получим следующее уравнение:
,
тогда получим следующее уравнение:
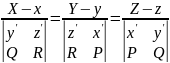
Уравнение спрямляющей плоскости
Для спрямляющей плоскости вектором нормали является направляющий вектор главной нормали, поэтому получим следующее уравнение:

В
b
ыпишем теперь натуральную систему координат (орты сопровождающего трехгранника – триэдраn