Радиус кривизны кривой. Центр кривизны кривой. Круг кривизны кривой (для плоской кривой)
Рассмотрим
плоскую кривую ℒ
с кривизной
.
В малой окрестности точки
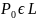кривую можно заменить ее касательной
прямой в этой точке. Это первое приближение.
Второе приближение кривой является
соприкасающаяся окружность (вернее её
малая дуга).
Расположим
оси координат так, что начало координат
совпадет с т.
и ось Ох казалась кривой ℒ
в этой точке. Пусть у = у(х) – уравнение
кривой, а
- уравнение окружности проходящей через
т.
.
Def.
Окружность
называется соприкасающейся, если в т.
х = 0 совпадают между собой значения
функции у(х) и
и их первых и вторых производных, т. е.
(функции
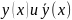совпадают с точкой О(
)).
Следствие: 1)Касательные совпадают в т.
2) Кривизны совпадают в
Def.
Радиус окружности
- и называется радиусом кривизны кривой
ℒ
в т.
.
Центр соприкасающейся окружности………….
Радиус и центр кривизны кривой
На предыдущей лекции мы выяснили, что радиус и центр соприкасающейся окружности (или окружности кривизны) и является радиусом и центром кривизны кривой. Выясним их математический смысл.
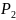
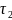
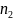
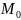
M
,
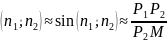тогда
Отрезок
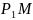называют радиусом кривизны,
.
Получили, что
.
Def
(центр кривизны). Точку М0
как точку пересечения 2-х нормалей кривой
выходящих из точек
и
при
стремлении
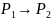называют центром кривизны кривой центр
кривизны кривой находят на нормали
кривой проведенной в данной т.
на
расстоянии обратном к кривизне кривой
в этой точке
.
Выводим формулы для координат центра кривизны:
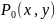
R
1)
центр кривизны принадлежит нормали
кривой построенной в т.
,
т.е.
2) центр кривизны является центром соприкасающейся окружности, т.е.
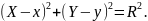
Решаем совм-ю систему:
и
.
Получим
следующие координаты центра кривизны:
(учитывая, что
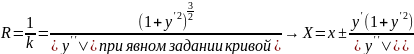и
Для
выяснения знака надо рассмотреть случаи,
когда
и
.
Если
,
то кривая выпукла вниз. Следовательно,
и надо взять нижние знаки.
Замечание.
Если кривая задана параметрическими
уравнениями: х = х(t),
y
= y(t),
то подставим в формулу (**) значения
и
получаем
и
.
Определения.1) Множество всех центров кривизны данной линии называется эволютой.
2) По отношению к своей эволюте исходная линия называется эвольвентой (или разверткой)
Пример:
.
Найти её эволюту.
2
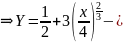уравнение
эволюты
Геометрия пространственных кривых
Для натуральной системы координат.
При построении пространственной системы координат, связанной с кривой, за начало координат берут любую точку на кривой, а за оси ДПСК следующие: за ось абсцисс принимают касательную в этой точке, за ось ординат – главную нормаль, а за ось аппликат – бинормаль. За координатные плоскости выбирают: соприкасающуюся, нормальную и спрямляющую плоскости.
b
P
спрямл
норм
n
сопр
Способы задания пространственных кривых:
Способ задания |
Кривая |
Векторно-параметрический |
|
Параметрический |
|
Явный |
|
Как пересечение 2-х поверхностей |
|
1) Касательная к пространственной кривой:
R(t)
O
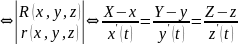
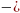каноническое
уравнение касательной
Получим уравнение касательной и кривой как пересечение поверхностей:
.
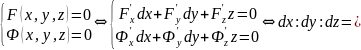
Тогда заменяя производные дифференциалами в уравнении касательной, получим:
.
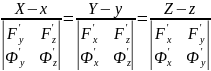2) Нормальная плоскость и её уравнение:
r
R
O
Def. Множество нормалей, проведенных к данной точке на кривой, образуют нормальную плоскость.
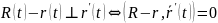(векторное
уравнение плоскости)
или
если
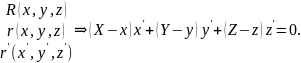
В случае, когда кривая задана неявно как пересечение двух плоскостей, уравнение нормальной плоскости следующее:
N
.3) Соприкасающаяся плоскость
R(t)
r(t)
L
Рассмотрим
дважды непрерывно дифференцируемую
кривую L
и т.
.
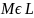В точке М определены векторы
- вектор касательной и
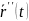- вектор …. Если они не коллинеарны, то
они и определены уравнениями соприкасающейся
плоскости:
или
.