Параметризация кривой

Задания кривой с помощью радиус-вектора (векторно-параметрически) означает, что каждому числовому заданию параметра t мы ставим в соответствие вектор r=r(t). Если собрать все точки этих векторов в одну точку, то концы этих векторов опишут кривую, годограф вектор-функции. Таким образом между типовыми значениями параметра t и точками на кривой установлено взаимно-однозначное соответствие. Такое соответствие и называется параметризацией кривой.

Замечание. Параметризовать кривую можно не единственным образом, если параметр t = f(u), где f = f(u) – непрерывная монотонная (иногда возрастающая) функция, то мы получим новую параметризацию кривой с помощью вектор – функции r = r(t) = r(f(u)).

Пример. (единичная окружность)

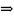
Определение. Будем называть кривую L – регулярной (n–раз дифференцируемой) без особых точек, если эта кривая допускает параметризацию с помощью параметра t такую, что вектор-функция r = r(t) n–раз дифференцируема ( ) и 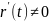при всех значениях параметра 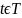. В частности рассматриваем кривые, класс гладкости которых n=1, 2 или 3.

Аналитические способы задания плоских (пространственных) кривых.

def. Кривая называется плоской, если все ее точки принадлежат некоторой плоскости.

Способ задания	Кривая
Явный	y = f(x)
Неявный	F(x,y) =0 (*)
Параметрический
Векторно-параметрический

Замечание. Если между решением уравнения (*) и точками кривой существует взаимно-однозначное соответствие, то уравнение определяет кривую .

Способы аналитического задания (образования) кривых

1. Как линии пересечения данной поверхности и данной плоскости.

2. Как геометрическое место точек (ГМТ) обладающих данным свойством.

3. Как траектория точки, характер движения которой известен (….).

4. По способу сопряжения проективно соответствующих элементов.

5. Заданием ее дифференциальных свойств ( как положительное решение некоторого дифференциального уравнения).

6. В результате геометрического преобразования уже известной кривой.

7. Аналитический способ задания (в виде решения уравнения).

Пример. Указать, какие линии задаются уравнением в ПСК:

1. ,

.

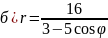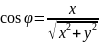Способ 1. Используя зависимость и , переходим в ДПС и преобразовываем кривую к каноническому виду.

Способ 2. В общем виде уравнения кривой 2-го порядка равенство , где р – фокальный параметр, - эксцентриситет и - положительный угол.

Тогда (из уравнения случай б)) Но отрезок. гипербола. .

Касательная к кривой (в частности плоской)

Q M ℒ

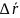
Р

r(t)

Def (касательной). Прямая PQ к которой стремится секущая PH при H – P (по кривой) называется касательной к кривой в точке Р.

Теорема. Гладкая кривая (n=1) 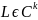без особых точек имеет в любой точке Р касательную.

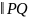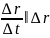Замечание. Покажем, что вектор (вычисляемый в точке Р) является направляющим вектором …. к кривой ( ).

: и при , т. е. в силу дифференцируемости r(t) в т. Р ( ) … предел и с другой стороны секущая при переходит в касательную.

Тогда (из аналитической геометрии) уравнения касательной к кривой

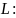
а) в векторно-параметрической форме: , – параметр

б) в параметрической форме: (т.к.

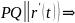
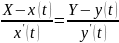
или

.

в) кривая заданная явным уравнением: y = f(x). Параметризуя это уравнение: и используя предыдущую формулу, получаем:

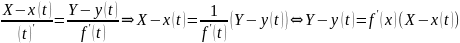
г) кривая задана неявным уравнением: F(x,y) =0. Из математического анализа: 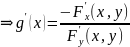и 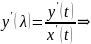подстав. в …

.