11. Розрахунок балок на ударну дію
Теоретичні відомості
Задачі на удар, згідно з технічною теорією удару, розв’язуються при таких допущеннях:
1. Матеріал пружної системи (елементу конструкції, що розраховується) при деформаціях, викликаних ударним навантаженням, слідує закону Гуку. Система є лінійно-деформованою, при цьому модуль пружності має те ж значення, що і при статичному навантаженні.
2. Кінетична енергія падаючого тіла повністю переходить в потенційну енергію деформації елементу конструкції, тобто не враховуються місцеві деформації.
3. Маса пружної системи (елементу конструкції), що сприймає дію ударного навантаження, мала в порівнянні з масою падаючого тіла, тобто система розглядається як невагома.
4. Удар вважається непружним, тобто після зіткнення падаючого тіла з системою він не відскакує, а при її деформації рухається з нею спільно.
З
алежно
від напрямку прикладання ударного
навантаження до стержня розрізняють
поздовжній, поперечний і крутильний
удари.
Мал. 38. Види ударів
Поздовжній удар – удар, при якому напрям сили паралельний до осі стержня (мал. 38, а). Він може бути розтягуючим, або стискуючим.
Поперечний удар – удар, при якому діючої напрям сили перпендикулярний до осі стержня (мал. 38, б).
Крутильний удар – удар, в результаті якого під дією зовнішніх сил виникає скручуючий момент відносно осі стержня (мал. 38, в).
Матеріали конструкції інакше реагують на ударні навантаження, ніж на статичні. Відбувається значне зменшення пластичності матеріалу з одночасним збільшенням значень механічних характеристик міцності.
Рекомендації до розв’язання задачі №11
1. При розв’язанні задач на ударну дію необхідно прикласти статичну силу, рівну вазі падаючого вантажу і побудувати епюру згинаючих моментів.
2. По епюрі згинаючих моментів треба знайти максимальний згинаючий момент і обчислити максимальну напругу.
3. Переміщення і напруження, викликані дією ударного навантаження, дорівнюють переміщенням і напруженням від цього ж статично прикладеного навантаження, помноженим на динамічний коефіцієнт:
;
,
(11.1)
де kД – динамічний коефіцієнт
, (11.2)
h – висота, з якої падає вантаж.
4. Найбільше нормальне напруження в поперечному перерізі балки при статичному навантаженні обчислюється за формулою:
.
(11.3)
Статичний прогин в точці удару визначається за правилом Верещагіна. Для цього будується епюра згинаючих моментів від одиничного навантаження, прикладеного в точці удару з подальшим перемножуванням на епюру згинаючих моментів від статичної сили, що дорівнює вазі падаючого тіла.
Приклад розв’язання задачі №11
На сталеву балку двотаврового поперечного перерізу з висоти h = 10 см посередині прольоту падає вантаж масою т = 100 кг (мал. 39).
М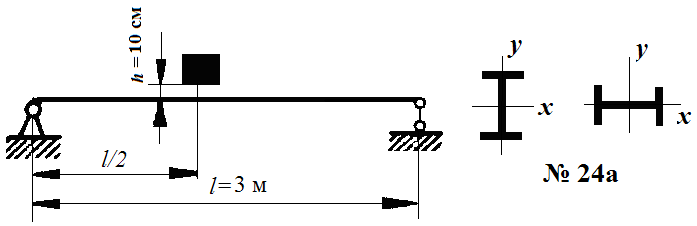
ал.
39. Балка під дією ударного навантаження
Зіставити найбільші статичну і динамічну напруження в поперечному перерізі балки і прогини під вантажем для випадків згину балки в площині найбільшої і найменшої жорсткості.
Розглянемо спочатку випадок згину балки в площині найбільшої жорсткості. Визначимо найбільше нормальне напруження в поперечному перерізі балки:
Момент опору і момент інерції поперечного перерізу двотавра 24а в площині найбільшої жорсткості відповідно
.
Прогин в середині прольоту балки при статичному навантаженні
де Е = 2∙105 МПа – модуль пружності сталі.
Динамічний коефіцієнт
Динамічний прогин і динамічне напруження визначимо по формулах:
Момент опору і момент інерції поперечного перерізу двотавра 24а в площині найменшої жорсткості відповідно
.
Нормальне напруження в поперечному перерізі балки:
Динамічний прогин і динамічне напруження
При статичній дії навантаження напруження в другому випадку більше, ніж в першому в 7,63 разу, а при її ударній дії – лише в 2,36 разу. Ця відмінність пояснюється тим, що в другому випадку жорсткість балки у 14,6 разу менша, ніж в першому, що приводить до істотного зменшення динамічного коефіцієнта.