
- •Вариант 2
- •Решить матричное уравнение
- •Вариант 3
- •Решить матричное уравнение
- •Вариант 4
- •Решить матричное уравнение
- •Найти общее решение системы линейных уравнений и все базисные решения
- •Написать общие уравнения прямых, проходящих через:
- •Точку под углом к оси ;
- •Вариант 5
- •Решить матричное уравнение
- •Вариант 6
- •Решить матричное уравнение
- •Найти общее решение системы линейных уравнений и все базисные решения
- •Написать общие уравнения прямых, проходящих через:
- •Точку под углом к оси ;
- •Вариант 7
- •Решить матричное уравнение
- •Вариант 8
- •Решить матричное уравнение
- •Вариант 9
- •Решить матричное уравнение
- •Вариант 10
- •Решить матричное уравнение
Решить матричное уравнение
(5E-A)•X•B = 4•C,
где A=
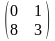 ,
B=
,
B=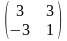 ,
C=
,
C=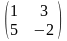 .
.
Предприятие специализируется по выпуску изделий трех видов: A, B, C; при этом используется сырье трех типов: S1, S2, S3. Нормы расхода каждого вида сырья на единицу изделия каждого вида и объем расхода сырья на 1 день заданы таблицей:
-
Вид сырья
Расходы сырья на единицу продукции, усл. ед.
Запасы сырья на один день, усл. ед.
A
B
C
S1
2
3
2
1700
S2
4
2
2
1800
S3
2
1
5
1700
Найти ежедневный объем выпуска изделий каждого вида.
Получить систему уравнений и решить ее тремя способами: по формулам Крамера, с помощью обратной матрицы и методом Гаусса.
 Исследовать
совместность, найти общее решение и
одно частное решение системы уравнений
Исследовать
совместность, найти общее решение и
одно частное решение системы уравнений
x1 - 2x2 +3x3 - 4x4 +2x5= 0
x1 +2x2 - x3 - x5= 1
x1 - x2 +2x3 - 3x4 = -1
x2 - x3 + x4 - 2x5= -1
Найти общее решение системы линейных уравнений и все базисные решения
-3x1 + x2 - 4x3 + 2x4= 9
5x1 - 2x2 + 7x3 - 3x4= -15
По заданным векторам
 ,
,
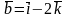 ,
,
 найти:
найти:
а)
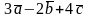 ;
б)
;
в)
;
г)
;
д) орт вектора
;
е) угол между векторами
и
;
б)
;
в)
;
г)
;
д) орт вектора
;
е) угол между векторами
и
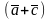 ;
ж)
.
;
ж)
.
Дана пирамида с вершинами в точках
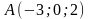 ,
,
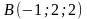 ,
,
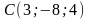 ,
,
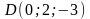 .
Найти: а) длину ребра
;
б) косинус угла между ребрами
.
Найти: а) длину ребра
;
б) косинус угла между ребрами
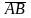 и
и
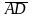 ;
в) объем пирамиды.
;
в) объем пирамиды.Написать общие уравнения прямых, проходящих через:
Точку
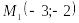 под углом
к оси
;
под углом
к оси
;Точки и
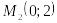 ;
;Точку параллельно оси абсцисс;
Точку перпендикулярно вектору
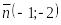 ;
;Точку параллельно вектору
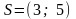 ;
;Найти расстояние от точки до прямой
![]() .
.
Привести уравнение кривой
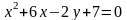 к каноническому виду и построить кривую.
Найти фокусы,
вершины линий,
эксцентриситет, уравнения директрис
и асимптот (если они есть).
к каноническому виду и построить кривую.
Найти фокусы,
вершины линий,
эксцентриситет, уравнения директрис
и асимптот (если они есть).
Построить в полярной системе координат линию
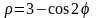 .
.
Вариант 8
Предприятие выпускает m видов изделий с использованием k видов сырья. Нормы расхода сырья для производства единицы продукции каждого вида даны матрицей Аm×k. Стоимость единицы сырья задана матрицей С. Найти затраты каждого вида сырья при заданном плане выпуска Q и суммарные затраты на сырье. Представить результаты с помощью матриц A, C, Q.
А=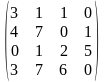 С=
С=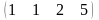 Q=
Q=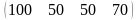
Решить матричное уравнение
(2E+A)•X•B2
= 6E+C, где A=
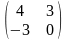 ,
B=
,
B=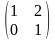 ,
C=
,
C=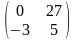 .
.
Предприятие специализируется по выпуску изделий трех видов: A, B, C; при этом используется сырье трех типов: S1, S2, S3. Нормы расхода каждого вида сырья на единицу изделия каждого вида и объем расхода сырья на 1 день заданы таблицей:
-
Вид сырья
Расходы сырья на единицу продукции, усл. ед.
Запасы сырья на один день, усл. ед.
A
B
C
S1
5
2
2
2300
S2
3
4
2
2100
S3
4
2
1
1800
Найти ежедневный объем выпуска изделий каждого вида.
Получить систему уравнений и решить ее тремя способами: по формулам Крамера, с помощью обратной матрицы и методом Гаусса.
Исследовать совместность, найти общее решение и одно частное решение системы уравнений
x1 + 3x2 +2x3 - 2x4 + x5 =5
x1 - 2x2 + x3 - x4 - x5 = -2
x1 - 4x2 + x3 + x4 - x5 = -2
3x1 - 3x2 + 4x3 - 2x4 - x5 = 1
Найти общее решение системы линейных уравнений и все базисные решения
x1 + x2 - x3 + x4 = 2
x1 + 2x2 - 2x3 + 4x4 = 3
По заданным векторам
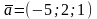 ,
,
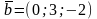 ,
,
 найти:
найти:
а)
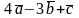 ;
б)
;
в)
;
б)
;
в)
 ;
г)
;
д) направляющие косинусы вектора
;
е) угол между векторами
и
;
ж)
;
г)
;
д) направляющие косинусы вектора
;
е) угол между векторами
и
;
ж)
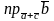 .
.
Дана пирамида с вершинами
 ,
,
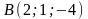 ,
,
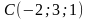 ,
,
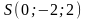 .
Найти:
.
Найти:
а) длину ребра
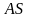 ;
б) площадь грани
;
в) объем пирамиды.
;
б) площадь грани
;
в) объем пирамиды.
Написать общие уравнения прямых, проходящих через:
Точку
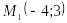 под углом
под углом
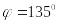 к оси
;
к оси
;Точки и
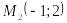 ;
;Точку параллельно оси абсцисс;
Точку перпендикулярно вектору
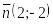 ;
;Точку параллельно вектору
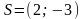 ;
;Найти расстояние от точки до прямой
![]() .
.
Привести уравнение кривой
 к каноническому виду и построить
кривую. Найти
фокусы, вершины линий,
эксцентриситет, уравнения директрис
и асимптот (если они есть).
к каноническому виду и построить
кривую. Найти
фокусы, вершины линий,
эксцентриситет, уравнения директрис
и асимптот (если они есть).Построить в полярной системе координат линию
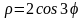 .
.
