3.5 Общая схема исследования функции и построение графика функции.
1. Найти область определения функции.
2. Найти точки пересечения графика с осями координат
3. Найти интервалы знакопостоянства функции.
4. Установить чётность и периодичность функции.
5. Найти асимптоты графика функции.
6. Найти интервалы монотонности и экстремумы функции.
7. Найти интервалы выпуклости, вогнутости и точки перегиба графика функции.
8. Построить график функции.
3.6 Наибольшее и наименьшее значения функции на отрезке.
Пусть функция
непрерывна на отрезке
.
Тогда на этом отрезке она достигает
своих наибольшего и наименьшего
значений. Эти значения функция может
принять либо во внутренней точке
отрезка
,
либо на границе отрезка, т.е. при
или
.
Если
,
то точку
следует искать среди критических точек
данной функции.
Получаем следующее правило нахождения наибольшего и наименьшего значений функции на :
1. найти критические точки функции на интервале ;
2. вычислить значения функции в найденных критических точках;
3. вычислить значения функции на концах отрезка, т.е. в точках и ;
4. среди всех вычисленных значений функции выбрать наибольшее и наименьшее.
4. Индивидуальные задания для контрольной работы
Задача №1. Вычислить предел.
1.1. а)
;
б)
;
в)
г)
1.2 а)
;
б)
;
в)
г)
1.3 а)
;
б)
;
в)
г)
1.4 а)
;
б)
;
в)
г)
1.5 а)
;
б)
;
в)
г)
1.6 а)
;
б)
;
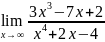в)
г)
1.7 а)
;
б)
;
в)
г)
1.8 а)
;
б)
;
в)
г)
1.9 а)
;
б)
;
в)
г)
1.10 а)
;
б)
;
в)
г)
1.11 а)
;
б)
;
в)
г)
1.12 а)
;
б)
;
в)
г)
1.13 а)
;
б)
;
в)
г)
1.14 а)
;
б)
;
в)
г)
1.15 а)
;
б)
;
в)
г)
1.16 а)
;
б)
;
в)
г)
1.17 а)
;
б)
;
в)
г)
1.18 а)
;
б)
;
в)
г)
1.19 а)
;
б)
;
в)
г)
1.20 а)
;
б)
;
в)
г)
Задача №2. Найти производную
функции
.
2.1
а)
;
б)
;
в)
г)
2.2 а)
;
б)
;
в)
г)
2.3 а)
;
б)
;
в)
г)
2.4 а)
;
б)
;
в)
г)
2.5 а)
;
б)
;
в)
г)
2.6 а)
;
б)
;
в)
г)
2.7 а)
;
б)
;
в)
г)
2.8 а)
;
б)
;
в)
г)
2.9 а)
;
б)
;
в)
г)
2.10 а)
;
б)
;
в)
г)
2.11 а)
;
б)
;
в)
г)
2.12 а)
;
б)
;
в)
г)
2.13 а)
;
б)
;
в)
г)
2.14 а)
;
б)
;
в)
г)
2.15 а)
;
б)
;
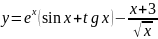в)
г)
2.16 а)
;
б)
;
в)
г)
2.17 а)
;
б)
;
в)
г)
2.18 а)
;
б)
;
в)
г)
2.19 а)
;
б)
;
в)
г)
2.20 а)
;
б)
;
в)
г)
Задача №3. Найти дифференциал
функции
.
.
Задача №4. Вычислить приближенно с помощью дифференциала.
.
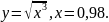
Задача №5. Составить уравнения касательной и нормали к данной кривой в точке с абсциссой
.
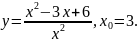
Задача №6. Найти
производную второго порядка
:
Задача №7. а) найти наибольшее и наименьшее значения функции на заданном промежутке.
б) провести полное исследование функции и построить её график.
