3. Правило подсчёта цифр.

При вычислении этим методом составляется обычная расчётная таблица, явный учёт погрешностей не ведётся, округления результатов промежуточных действий проводятся по следующим правилам:

1. при сложении и вычитании приближённых чисел следует округлить число с меньшей абсолютной погрешностью (для десятичных дробей с большим количеством знаков после запятой) так, чтобы в нём осталось на один-два разряда больше, чем в точном числе. В результате считать верными столько десятичных знаков после запятой, сколько их в приближённом данном с наименьшим числом десятичных знаков после запятой;

1. при умножении и делении двух приближённых чисел нужно округлить число с большим количеством значащих цифр так, чтобы в нём было лишь на одну значащую цифру больше, чем в другом числе. В результате считать верными столько значащих цифр, сколько их в приближённом данном с наименьшим числом значащих цифр;

2. в значениях элементарных функций от приближённых значений аргумента (включая возведение в степень, извлечение и т.д.) в результате можно считать верными столько значащих цифр, сколько верных значащих цифр имеет значение аргумента;

3. при записи промежуточных результатов следует сохранять на одну цифру больше, чем рекомендуют правила 1-3. В окончательном результате эта запасная цифра округляется.

4. Систематический учёт погрешностей.

Метод предусматривает поэтапный подсчёт границ погрешностей всех промежуточных и окончательного результатов по правилам вычисления погрешностей, рассмотренных выше. Промежуточные результаты, также как и их погрешности, заносятся в специальную расчётную таблицу, состоящую из двух параллельно заполняемых частей – для результатов и их погрешностей.

5. Метод границ.

В случае, когда не столь важно получить наиболее близкое к точному значению вычисляемой величины, сколь важно иметь абсолютно-гарантированные границы её возможных значений применяют метод границ, суть которого в следующем. Для функции u=f(x,y) из аргументов x и y необходимо вычислить f(a,b), где a и b – приближённые значения аргументов, причём совершенно точно известно, что НГ_a<a<ВГ_a, НГ_b<b<ВГ_b, где НГ и ВГ – соответственно обозначения нижней и верхней границы значений, и тогда

f(НГ_a, НГ_b)<f(a,b)< f(ВГ_a, ВГ_b),

если f возрастает по a и b, и

f(НГ_a, ВГ_b)<f(a,b)< f(ВГ_a, НГ_b),

если f возрастает по a и убывает по b.

В частности, для положительных аргументов

f(a,b)=a+b, то НГ_a + НГ_b <a+b< ВГ_a + ВГ_b;

f(a,b)=a-b, то НГ_a - ВГ_b <a-b< ВГ_a - НГ_b;

f(a,b)=a*b, то НГ_a * НГ_b <a*b< ВГ_a * ВГ_b;

f(a,b)=a/b, то НГ_a /ВГ_b <a/b< ВГ_a /НГ_b .

Расчётная граница метода имеет две строки для вычисления НГ и ВГ выражения.

Задание 1. Верные цифры

1. Определить, какое равенство точнее.

2. Округлить сомнительные цифры числа, оставив верные знаки: а) в узком смысле; б) в широком смысле. Определить абсолютную погрешность результата.

3. Найти предельные абсолютные и относительные погрешности чисел, если они имеют только верные цифры: а) в узком смысле; б) в широком смысле.

Образец выполнения задания

1. 

2. а) б) 2,3544;

3. а) 0,4357; б) 12,384

1. Находим значения данных выражений с большим числом десятичных знаков: . Затем вычисляем предельные абсолютные погрешности, округляя их с избытком:

Предельные относительные погрешности составляют

Так как то равенство является более точным.

2. а) Пусть Согласно условию, погрешность ; это означает, что в числе 72,353 верными в узком смысле являются цифры 7, 2, 3. По правилам округления найдем приближенное значение числа, сохранив десятые доли:

Полученная погрешность больше 0,05; значит, нужно уменьшить число цифр в приближенном числе до двух:

Так как то обе оставшиеся цифры верны в узком смысле.

б) Пусть а=2,3544; тогда В данном числе верными в широком смысле являются три цифры, поэтому округляем его, сохраняя эти три цифры:

; полная погрешность .

Значит, и в округленном числе 2,35 все три цифры верны в широком смысле.

3. а) Так как все четыре цифры в числе а=0,4357 верны в узком смысле, то абсолютная погрешность не превосходит половины единицы младшего разряда , а относительная погрешность

б) Так как все пять цифр числа а=12,384 верны в широком смысле, то ;

Индивидуальные задания

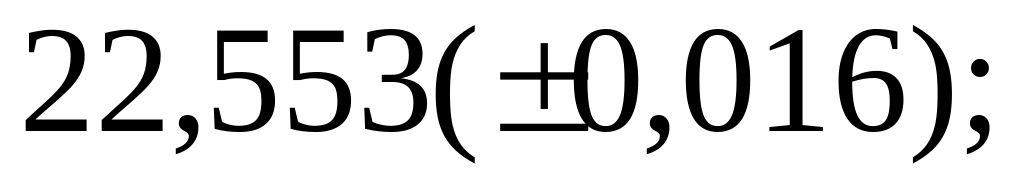
Вариант 1 1) 2) а) б) 3) а) 0,2387; б) 42,884.	Вариант 2 1) 2) а) б) 3) а) 3,751; б) 0,537.
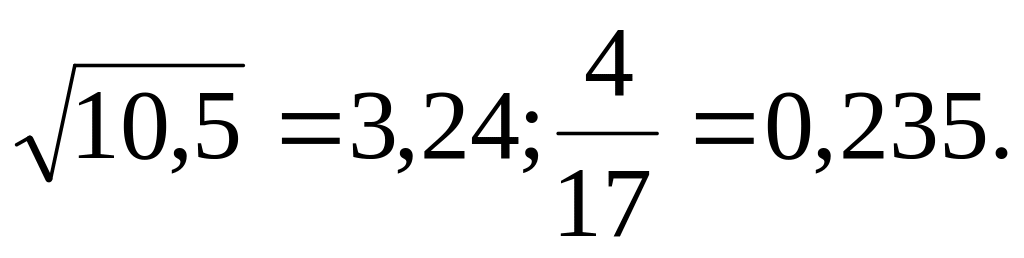
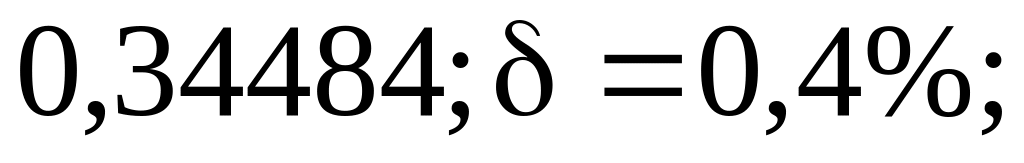
Вариант 3 1) 2) а) б) 3) а) 11,445; б) 2,043.	Вариант 4 1) 2) а) б) 3) а) 2,3445; б) 0,745.
Вариант 5 1) 2) а) б) 3) а) 8,345; б) 0,288.	Вариант 6 1) 2) а) б) 3) а) 12,45; б) 3,4453.
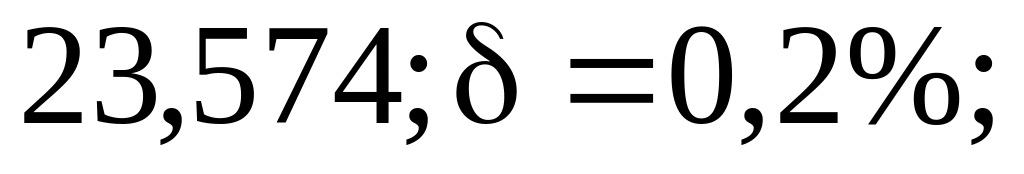
Вариант 7 1) 2) а) б) 3) а) 0,374; б) 4,348.	Вариант 8 1) 2) а) б) 3) а) 20,43; б) 0,576.
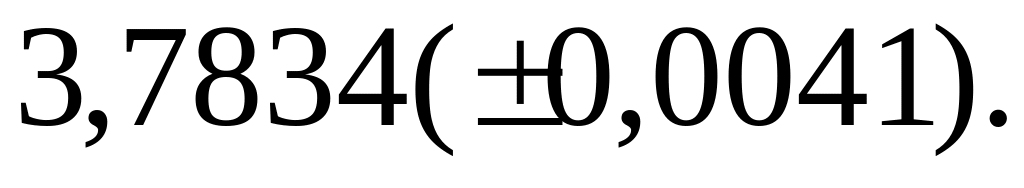
Вариант 9 1) 2) а) б) 3) а) 41,72; б) 0,678.	Вариант 10 1) 2) а) б) 3) а) 5,634; б) 0,0748.
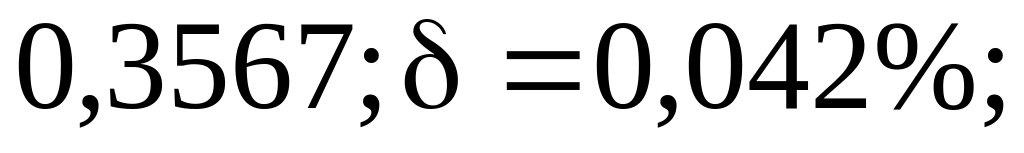
Вариант 11 1) 2) а) б) 3) а) 18,357; б) 2,16.	Вариант 12 1) 2) а) б) 3) а) 0,5746; б) 236,58.
Вариант 13 1) 2) а) б) 3) а) 14,862; б) 8,73.	Вариант 14 1) 2) а) б) 3) а) 0,3648; б) 21,7.
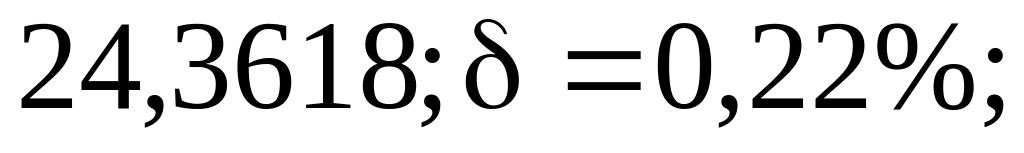
Вариант 15 1) 2) а) б) 3) а) 2,4516; б) 0,863.	Вариант 16 1) 2) а) б) 3) а) 62,74; б) 0,389.
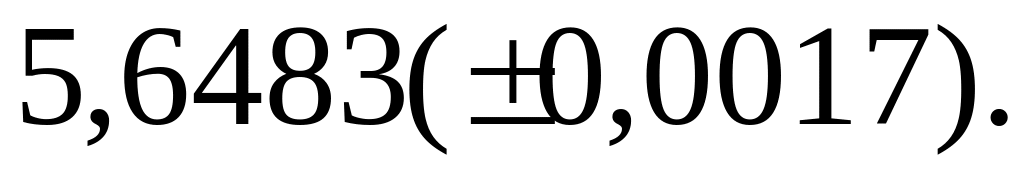
Вариант 17 1) 2) а) б) 3) а) 5,6432; б) 0,00858.	Вариант 18 1) 2) а) б) 3) а) 0,0384; б) 63,745.
Вариант 19 1) 2) а) б) 3) а) 12,688; б) 4,636.	Вариант 20 1) 2) а) б) 3) а) 6,743; б) 0,543.
Вариант 21 1) 2) а) б) 3) а) 15,644; б) 6,125.	Вариант 22 1) 2) а) б) 3) а) 0,3825; б) 24,6.
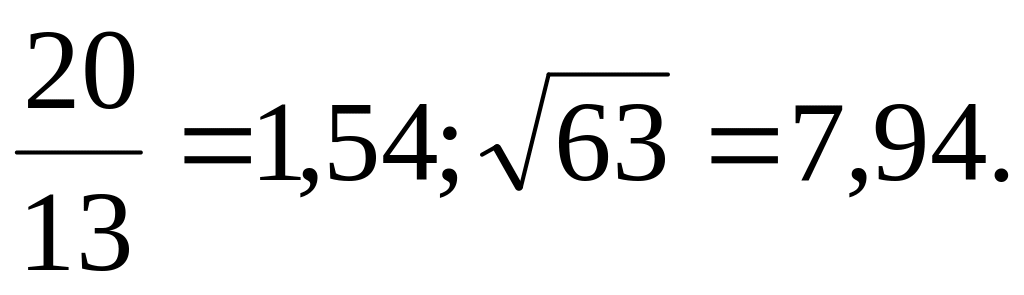
Вариант 23 1) 2) а) б) 3) а) 16,383; б) 5,734.	Вариант 24 1) 2) а) б) 3) а) 0,573; б) 3,6761.
Вариант 25 1) 2) а) б) 3) а) 18,275; б) 0,00644.	Вариант 26 1) 2) а) б) 3) а) 3,425; б) 7,38.
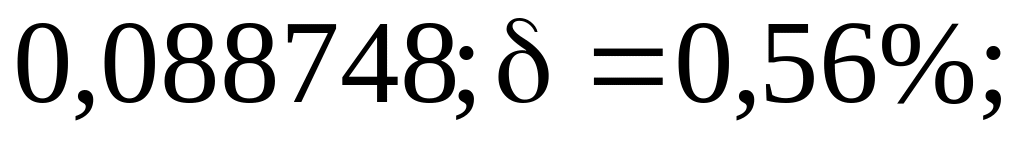
Вариант 27 1) 2) а) б) 3) а) 3,75; б) 6,8343.	Вариант 28 1) 2) а) б) 3) а) 3,643; б) 72,385.
Вариант 29 1) 2) а) б) 3) а) 26,3; б) 4,8556.	Вариант 30 1) 2) а) б) 3) а) 43,813; б) 0,645.