1.7. Исследование инут

Соберите схему, приведённую на рис.1.25 в пакете EWB.

Р ис. 1.25. Исследование ИНУТ

Изменяя сопротивление резистора R путём изменения положения движка этого резистора, записать показания амперметра М₁ и вольтметра М₂ в табл.1.7.

Таблица 1.7 - Исследование ИНУТ

n	R,Ом	U,В	I,mA	Rупр,Ом
1	200
2	400
3	600
4	800
5	1000

По результатам измерений (см. табл.1.7) построить внешнюю характеристику ИНУТ U(I). Определить управляющее сопротивление R_упр=U₂/I₁.

Контрольные вопросы

1. Перечислите основные этапы формирования электрической схемы в пакете EWB.

2. Опишите структуру интерфейса EWB.

3. Какие опции содержат разделы горизонтального меню?

4. Каким образом осуществляется вставка элементов электрической цепи и как выполняются соединения между их выводами?

5. Как назначаются значения параметрам элементам электрической цепи?

6. Каким образом проводится запуск программы на анализ?

7. Как выполняются настройки амперметра и вольтметра, выбранных с панели инструментов Indicators?

8. Перечислите все типы источников напряжения (ЭДС), имеющиеся в программе Electronics Workbench. Каковы их свойства и условные обозначения?

9. Перечислите все типы источников тока, имеющихся в программе Electronics Workbench. Каковы их свойства и условные обозначения?

10. Чему равно внутреннее сопротивление источника напряжения и источника тока?

11. Чем отличается неидеальные источники электрической энергии от идеальных?

12. Как осуществить эквивалентное преобразование неидеального источника напряжения в неидеальный источник тока и обратное преобразование?

13. Какие режимы работы неидеального источника Вы знаете?

14. Что такое режим холостого хода и короткого замыкания реального источника?

15. Что такое согласованный режим реального источника?

16. При каком сопротивлении нагрузки в ней выделяется максимальная мощность?

17. Какие типы зависимых источников Вам известны?

Лабораторная работа № 2 Тема: «Исследование простых линейных электрических цепей постоянного тока»

Цель работы – Ознакомиться с методами расчета простых электрических цепей постоянного тока.

Теоретические сведения

2.1. Основные понятия об электрической цепи

Электрической цепью называют совокупность соединённых друг с другом источников электрической энергии и нагрузок, по которым может протекать электрический ток. Графическое изображение такой цепи с помощью условных знаков, отражающее реальную взаимосвязь всех элементов между собой, называется принципиальной схемой.

В устройствах для генерирования электрической энергии (источниках электрической энергии) возбуждается электродвижущая сила (ЭДС) в процессе преобразования различных видов энергии в электрическую. Каждый источник характеризуется ЭДС и внутренним сопротивлением. Единицей измерения ЭДС является вольт (В), а сопротивления – ом (Ом).

В приёмниках происходит обратное преобразование электрической энергии в другие виды энергии: тепловую, механическую, световую, химическую и т. д. Приёмник энергии можно характеризовать рабочим напряжением, током, мощностью, а также сопротивлением.

Источники электрической энергии соединяются с приёмниками линиями электрической связи, которые на принципиальных схемах изображаются отрезками прямых. Сопротивление соединительных проводов в задачах считается равным нулю.

В замкнутой электрической цепи ЭДС источника создает ток. Цепь, в которой значение тока не зависит от времени, называется цепью постоянного тока. Обозначается такой ток прописной печатной буквой «I».

Если сопротивление элементов электрической цепи не зависит от тока или напряжения на них, то такие элементы называются линейными. Цепь, содержащая только линейные элементы, называется линейной. При наличии в цепи даже одного нелинейного элемента, сопротивление которого зависит от тока или напряжения, вся цепь считается нелинейной.

При решении некоторых задач используется величина, обратная сопротивлению, называемая проводимостью. Измеряется проводимость сименсами (См).

В простейшем случае, элементы цепи могут соединяться последовательно, параллельно и смешанно. Пример последовательного соединения приведен на рисунке 2.1, а. Во всех элементах, включённых последовательно, протекает один и тот же ток. Напряжение на элементах, включённых последовательно, прямо пропорционально их сопротивлению.

На рисунке 2.1, б дан пример параллельного соединения потребителей. При этом на всех элементах, включённых параллельно, действует одно напряжение, а токи в этих элементах обратно пропорциональны их сопротивлениям.

Отличительной чертой смешанного соединения является наличие в цепи участков с последовательным и параллельным соединениями. В качестве примера, на рисунке 2.1, в изображена цепь с пятью потребителями. Три из них (r1, r2, r3) включены последовательно, а два (r4, r5) параллельно. Следует отметить, что, несмотря на отсутствие непосредственного соединения потребителя r3 с потребителями r1 и r2, его также можно считать соединённым последовательно с первыми двумя. Это возможно потому, что по элементам r1, r2, r3 протекает один и тот же ток, а после подключения к зажимам цепи источника питания они входят в состав одной ветви. Через элементы r1, r2 ток входит на участок с потребителями r4, r5, а выходит из него через r3.

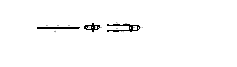Рисунок 2.1 – Способы соединения элементов в электрической цепи

В некоторых случаях элементы цепи могут соединяться по более сложным схемам, на рисунке 2.2 приведена схема, называемая мостовой. Цепь, на всех участках которой протекает один и тот же ток, называется неразветвлённой. Если же цепь содержит участки с различными токами, она является разветвлённой. На рисунке 2.3 приведён пример разветвлённой электрической цепи.

Рисунок 2.2 – Мостовая схема соединения	Рисунок 2.3 – Пример разветвлённой цепи

Электрические цепи могут быть простыми и сложными. Если цепь содержит только один источник электрической энергии, то такая цепь называется простой. К простым относятся и цепи, в которых есть несколько источников, но которые путём эквивалентных преобразований можно привести к виду с одним эквивалентным источником (рис. 2.4).

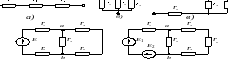
Рисунок 2.4 - Примеры простых электрических цепей

В электрической цепи можно выделить узлы, ветви и контуры. Ветвь – участок цепи, состоящий из одного или нескольких последовательно соединённых элементов, заключённый между двумя узлами. По всем элементам ветви протекает одинаковый ток. Узел – точка, где сходятся три и более ветви. Контур – любой замкнутый путь, образованный одной или несколькими ветвями. Независимыми контурами являются такие, при выборе которых в каждый последующий контур входит хотя бы одна новая ветвь, не входившая в предыдущие. В любой цепи содержатся ветви и контуры, а узлы присущи только разветвлённым цепям.

2.2 Основные законы электрических цепей.

При анализе простых и сложных цепей широко используются законы Ома, Кирхгофа, Джоуля–Ленца.

Закон Ома применяется для одного элемента, одной ветви или для одноконтурной замкнутой (не имеющей разветвлений) электрической цепи:

- для одного элемента или пассивной ветви ab (рис. 2.5)

Р исунок 2.5 - пассивная ветвь электрической цепи

Закон Ома для участка пассивной цепи:

где I – ток, проходящий через элемент цепи [A];

– приложенное к элементу (ветви) напряжение [B];

R – сопротивление [Ом].

- для активной ветви ab (рис. 2.6)

В общем случае, когда между узлами a и b включена активная резистивная ветвь и ток направлен от узла a к узлу b, закон Ома принимает вид:

, (2.1)

где - алгебраическая сумма ЭДС, при этом ЭДС, направления которых совпадают с направлением тока, берутся со знаком “+”, а если эти направления не совпадают, то соответствующие ЭДС берутся со знаком “–”.

Выражение (2.1) есть обобщенный закон Ома для участка цепи, содержащего источник ЭДС.

- для замкнутой одноконтурной цепи (рис. 2.7).

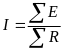, (2.2)

где – алгебраическая сумма ЭДС контура;

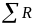– арифметическая сумма сопротивлений контура;

Рис. 2.7

Первый закон Кирхгофа применяется для узла электрической цепи. Формулируется он следующим образом: алгебраическая сумма токов, сходящихся в узле, равна нулю:

. (2.3)

В этом уравнении обычно принимают токи, направленные к узлу, со знаком минус, а выходящие из узла – со знаком плюс.

Второй закон Кирхгофа справедлив для контура электрической цепи и формулируется следующим образом: в любом замкнутом контуре электрической цепи алгебраическая сумма падений напряжений на участках цепи, входящих в этот контур, равна алгебраической сумме ЭДС в нем:

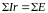(2.4)

В данном уравнении положительный знак для падения напряжения берётся в том случае, если направление тока, создающего это падение, совпадает с направлением обхода контура. В противном случае берется знак минус. Аналогично, если направление ЭДС совпадает с направлением обхода контура, то при алгебраическом суммировании эта ЭДС положительна. Направление обхода контура выбирается произвольно.

Закон Джоуля–Ленца позволяет определить количество тепловой энергии, которая выделяется на сопротивлении r при протекании по нему электрического тока:

где I – значение тока;

r – сопротивление нагрузки;

t – время протекания тока.

Для характеристики скорости превращения электрической энергии в тепловую используют мощность, выражение для которой можно получить из закона Джоуля–Ленца,:

.

Закон электромагнитной индукции устанавливает связь между индуктированным ЭДС в электрических цепях и изменением магнитного потока, пронизывающего поверхность, ограниченную контуром цепи, или индуктированное ЭДС в проводнике при пересечении им магнитного поля. В соответствии с этим законом ЭДС, индуктируемая в цепи при изменении магнитного потока, проходящего через поверхность, ограниченную контуром, равна скорости изменения магнитного потока, взятой с отрицательным знаком,

e= – dФ/dt ,

где Ф – магнитный поток;

t – время.

Уравнение баланса мощности:

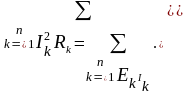0

Уравнение баланса мощности является модификацией закона сохранения энергии для электрических цепей. Это базовое уравнение для проверки правильности выполненных расчетов тех или иных цепей.

В левой части этого уравнения стоит арифметическая сумма мощностей, которые выделяются на сопро­тивлениях от токов, которые по ним протекают. В правой части – мощность, отданная источниками в сеть.

При этом возможна такая ситуация, когда одно из сла­гаемых суммы справа мо­жет оказаться отрицательным. Это будет означать, что в данной ситуации источник становится пот­ребителем. Она возникает в случае, когда ток, проте­кающий по источнику, направлен встречно направлению ЭДС.

2.3 Расчет простых цепей постоянного тока

Метод эквивалентных преобразований чаще всего применяют для электрической цепи с одним источником энергии. Преобразование части электрической цепи является эквивалентным, если оно не изменяет значения токов и напряжений в не преобразованной части цепи. Этот метод основан на постепенном упрощении цепи (т.н. «свертывание схемы») и нахождении одного эквивалентного сопротивления. При расчете токов в отдельных ветвях схему «развертывают» в обратном порядке. Упрощение электрической цепи или какого-либо участка производят таким образом, чтобы токи и напряжения в частях схемы, не подвергнутых преобразованию, остались неизменными. Такое преобразование называется эквивалентным, а схемы – эквивалентными. При этом мощности исходной цепи и преобразованной будут одинаковы.

Так несколько последовательно соединённых потребителей можно заменить одним, причём его эквивалентное сопротивление равно сумме сопротивлений потребителей, включённых последовательно. Для n потребителей можно записать:

r_э = r₁ +r₂+…+r_n , (2.5)

где r₁ , r₂, ..., r_n – сопротивления каждого из n потребителей.

При параллельном соединении n потребителей эквивалентная проводимость g_э равна сумме проводимостей отдельных элементов, включённых параллельно,

g_э= g₁ + g₂ +…+ g_n . (2.6)

Учитывая, что проводимость является обратной величиной по отношению к сопротивлению, можно эквивалентное сопротивление определить из выражения:

(2.7)

где r₁, r₂, ..., r_n – сопротивления каждого из n потребителей, включённых параллельно.

В частном случае, когда параллельно включены два потребителя r₁ и r₂ , эквивалентное сопротивление цепи

.

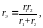Преобразования в сложных цепях, где отсутствует в явном виде последовательное и параллельное соединение элементов, начинают с замены элементов, включённых в исходной схеме треугольником, на эквивалентные элементы, соединённые звездой (или наоборот) рис. 2.8.

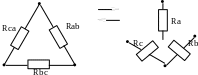
Рис. 2.8

Такие преобразования выполняют по формулам:

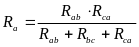
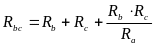
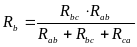
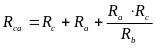
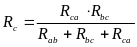
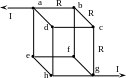
Для упрощения симметричных цепей используют прием объединения (или разъединения) равнопотенциальных точек (узлов). Так, для определения эквивалентного сопротивления между вершинами куба a и g R_ag (рис.2.9), равнопотенциальные точки b, d, c (c, f, n) можно объединить в один узел и тогда сопротивление R_ag можно определить по схеме, представленной на рис.2.10 (здесь все грани куба имеют равные сопротивления R).

R

Рис. 2.9

Видно, что эквивалентное сопротивление R_экв= R_ag определяется тремя параллельными группами (две по три и одна из шести сопротивлений), т.е. .

Для схемы, представленной на рис. 2.11 нужно, наоборот, разъединить ветви (сопротивление каждой ветви R) в узле m и тогда эквивалентное сопротивление цепи относительно зажимов ab составит .

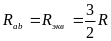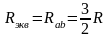
Преобразование источника ЭДС Е в эквивалентный источник тока J выполняется по схеме, приведенной на рис.2.12, а преобразование источника тока J в эквивалентный источник ЭДС Е – по схеме, приведенной на рис. 2.13.

Вынесение ЭДС за узел.

Рис. 2.14

Это преобразование поясняется рис. 2.14 В каждую ветвь, подходящую к узлу рис. 2.14,а можно включить ЭДС E, направленные, например, от узла рис. 2.14,б. В ветви с исходным источником появляется две равных по модулю и разнонаправленных ЭДС, которые можно сократить. В результате преобразований эквивалентная цепь представлена на рис. 2.14,в.

Замена источника тока эквивалентными источниками ЭДС.

Рассмотрим фрагмент цепи, в который входит контур, содержащий источник тока и ряд ветвей (рис. 2.15,а). Источник тока можно преобразовать в источники ЭДС (рис. 2.15,б), если в каждую ветвь контура включить дополнительный источник ЭДС, равный произведению тока источника тока на сопротивление ветви. Направление обхода контура выбирается по направлению источника тока, а направление ЭДС задаётся на встречу обхода контура.

Р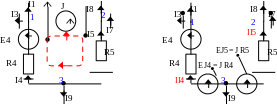 ис. 2.15

При практической реализации метода расчёта простой цепи с помощью преобразований выявляются в цепи участки с параллельным и последовательным соединением потребителей, а затем рассчитываются эквивалентные сопротивления этих участков. Если в исходной цепи в явном виде нет таких участков, то, применяя описанные ранее переходы от треугольника элементов к звезде или от звезды к треугольнику, проявляют их. Данные операции позволяют упростить цепь. Применив их несколько раз, приходят к виду с одним источником и одним эквивалентным потребителем энергии. Далее, применяя законы Ома и Кирхгофа, рассчитывают токи и напряжения на участках цепи.

Пример 2.1 – Расчёт разветвлённой электрической цепи постоянного тока.

В заданной цепи постоянного тока, изображённой на рисунке 2.16, определить токи ветвей.

Исходные данные для расчета:

E = 100 B, r₁ = 4 Ом, r₂ = 6 Ом, r₃ = 5 Ом, r₄ = 1 Ом , r₅ = 3 Ом.

Р исунок 2.16 – Схема разветвлённой электрической цепи постоянного тока

Для расчета задаёмся направлением токов всех ветвей и обозначаем эти токи на схеме. При определении направления тока следует учитывать тот факт, что ток в ветви течёт от большего потенциала к меньшему. Далее выполняем эквивалентные преобразования в цепи и последовательно упрощаем схему. Начинаем с замены двух последовательно включенных резисторов r₃ и r₄ одним эквивалентным. Схема упрощается и имеет вид, изображённый на рисунке 1.17, а.

Резистор r₃₄ рассчитывают следующим образом (при последовательном соединении r₃ и r₄): r₃₄ = r₃ + r₄ = 5+1= 6 Ом.

Дальнейшее упрощение схемы происходит в результате замены параллельно включенных резисторов r₂ и r₃₄ одним r₂₃₄ (рисунок 2.17, б). Эквивалентное сопротивление двух резисторов, включенных параллельно, можно определить из выражения (2.8):

r₂₃₄ = r₂r₃₄ / (r₂+r₃₄) = 6∙6 / (6+6) = 3 Ом.

Окончательное упрощение цепи происходит после замены трех последовательно соединенных резисторов r₁, r₂₃₄, и r₅ одним эквивалентным для всей цепи (рисунок 2.17, в):

r_э = r₁ + r₂₃₄ + r₅ = 4 + 3 + 3 = 10 Ом.

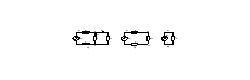Рисунок 2.17 – Эквивалентные схемы заданной цепи

В соответствии с законом Ома I₁ = E/r_э = 100/10 = 10 А.

Так как преобразования выполнялись эквивалентными, то ток I₁ будет одинаковым для всех цепей на рисунках 2.16 и 2.17.

Для определения токов I₂ и I₃ на участке после разветвления цепи необходимо найти напряжение U_ab между точками a и b, а затем, зная сопротивление ветвей, можно рассчитать токи в ветвях, включённых параллельно.

Межузловое напряжение U_ab находим из схемы, изображённой на рисунке 3.8, б. Здесь оно равно падению напряжения на резисторе r₂₃₄:

U_ab = I₁r₂₃₄ = 10 ∙ 3 = 30 В.

Токи после разветвления, на основании закона Ома, находим из выражений:

I₂ = U_ab/r₂ = 30 / 6 = 5 А, I₃ = U_ab / r₃₄ = 30 / 6 = 5 А.

Если подходящий к узлу ток разветвляется только на две ветви (как в данном примере), то путь нахождения токов после разветвления по известному току до разветвления можно сократить, исключая этап нахождения напряжения U_ab . Для такого частного случая можно воспользоваться формулой разброса. Структура формулы разброса – ток одной из ветвей после разветвления равен току до разветвления, умноженному на дробь. В числителе этой дроби – сопротивление соседней по отношению к определяемому току параллельной ветви, a в знаменателе – сумма сопротивлений ветвей, включенных параллельно.

Для определения тока I₂ формула разброса имеет вид

I ₂ = I₁ r₃₄/(r₂ + r₃₄) = 10 ∙ 6/ (6 + 6) = 5 A.

Третий ток в соответствии с этой формулой

I₃ = I₁r₂/(r₂ + r₃₄) = 10 ∙ 6/ (6 + 6) = 5 A.

Порядок выполнения лабораторной работы

1. В соответствие с номером варианта получить у преподавателя номиналы сопротивлений и источника для расчета схемы. Для расчета можно использовать математический пакет MathCad или другие программы для произведения расчетов.

2. Произвести в соответствии с методикой эквивалентные преобразования схемы.

3. Выполнить расчет эквивалентного сопротивления и общего тока в цепи.

4. В соответствии с описанной методикой расчета определить токи и напряжения на каждом из сопротивлений в цепи.

5. Собрать в пакете EWB схему в соответствии с вариантом.

6. Произвести моделирование работы схемы в среде EWB.

7. Измерить значения токов и напряжений на каждом из сопротивлений используя пакет моделирования EWB.

8. Все результаты расчета и моделирования занести в отчет по лабораторной работе, оформить отчет и сформулировать выводы по работе.

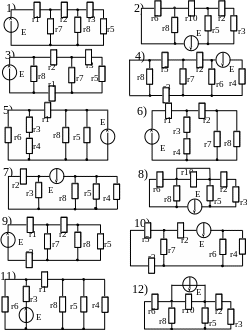
Индивидуальные задания

Контрольные вопросы

1. Что называют электрической цепью?

2. В чем измеряется сопротивление и проводимость цепи?

3. Какие существуют способы соединения элементов в электрической цепи?

4. Сформулируйте основные законы электрических цепей?

5. Сформулируйте правила получения эквивалентного сопротивления для последовательного и параллельного включения сопротивлений.

6. Назовите правила преобразования из соединения звездой в эквивалентное соединение треугольником и наоборот.

7. Сформулируйте алгоритм расчета методом эквивалентных преобразований.

ЛАБОРАТОРНАЯ РАБОТА № 3

Тема: «Метод непосредственного применения законов Кирхгофа»

Цель работы – Научиться рассчитывать электрические цепи на постоянном токе, используя законы Кирхгофа.

Теоретические сведения

4.1 Законы Кирхгофа

Первый закон Кирхгофа (закон токов). Алгебраическая сумма токов в любом узле равна нулю:

,

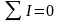или арифметическая сумма токов, входящих в узел, равна арифметической сумме токов, выходящих из узла.

Считая токи, входящие в узел, положительными, а выходящие – отрицательными для узла а (рис. 4.1) первый закон Кирхгофа можно записать следующим образом:

I₁ + I₂ – I₃ + I₄ = 0 или I₁ + I₂ + I₄ = I_3.

Рисунок 4.1 – Узел электрической цепи

Второй закон Кирхгофа (закон напряжений). Алгебраическая сумма напряжений на ветвях (элементах) любого замкнутого контура равна нулю:

,

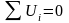или алгебраическая сумма ЭДС в любом замкнутом контуре равна алгебраической сумме падений напряжений на элементах этого контура:

(4.1)

Для составления уравнений по второму закону Кирхгофа вначале задают (указывают) направление токов во всех ветвях электрической цепи (если только токи не заданы по условию задачи) и для каждого контура выбирают направление обхода. Если при этом направление ЭДС совпадает с направлением обхода контура, то такую ЭДС в уравнении (4.1) берут со знаком “+”, если не совпадают – со знаком “–”. Падения напряжений в правой части уравнения (4.1) берут со знаком “+”, если выбранное направление тока ветви совпадает с направлением обхода контура, и со знаком “–”, если не совпадает.