2.2.. Оптимизация процесса работы механической мастерской
Для изготовления изделия в механической мастерской необходимо выполнить пять операции на машине и вернуться в точку первой операции. Эти операции могут быть произведены в любой последовательности. Однако время переналадки машины зависит от того, какой была предыдущая операция по изготовлению изделия. Длительности переналадок приведены в таблице 2.2. Какова наилучшая последовательность выполнения операций?
Таблица 2.11
Последующая операция
Предыдущая операция |
А |
Б |
В |
Г |
Д |
А |
|
15 |
20 |
5 |
10 |
Б |
15 |
|
30 |
25 |
12 |
В |
20 |
30 |
|
40 |
35 |
Г |
5 |
25 |
40 |
|
17 |
Д |
10 |
12 |
35 |
17 |
|
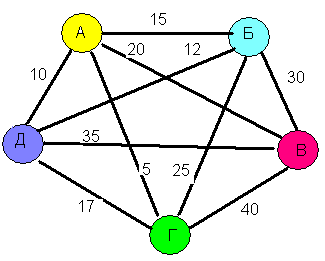
Рис. 2.3. Граф
2.2.1. Прямой алгоритм
;
;
;
;
;
;
;
;
;
И возвращаемся в точку А (+20)
;
Ответ: наилучшее время – 84. порядок обхода операций:
2.2.2. Метод Литтла
Табл. 2.12. исходная
|
А |
Б |
В |
Г |
Д |
А |
|
15 |
20 |
5 |
10 |
Б |
15 |
|
30 |
25 |
12 |
В |
20 |
30 |
|
40 |
35 |
Г |
5 |
25 |
40 |
|
17 |
Д |
10 |
12 |
35 |
17 |
|
Табл. 2.13. Зануление по столбцам
|
А |
Б |
В |
Г |
Д |
А |
|
10 |
15 |
0 |
5 |
Б |
3 |
|
18 |
13 |
0 |
В |
0 |
10 |
|
20 |
15 |
Г |
0 |
20 |
35 |
|
12 |
Д |
0 |
2 |
25 |
7 |
|
Табл. 2.14. Зануление по столбцам
|
А |
Б |
В |
Г |
Д |
А |
|
8 |
0 |
0 |
5 |
Б |
3 |
|
3 |
13 |
0 |
В |
0 |
8 |
|
20 |
15 |
Г |
0 |
18 |
20 |
|
12 |
Д |
0 |
0 |
10 |
7 |
|
Нижняя оценка: 5+12+20+5+10+2+15=69.
Табл. 2.15. Расчет оценок клеток
|
А |
Б |
В |
Г |
Д |
А |
|
8 |
|
|
5 |
Б |
3 |
|
3 |
13 |
|
В |
|
8 |
|
20 |
15 |
Г |
|
18 |
20 |
|
12 |
Д |
|
|
10 |
7 |
|
Шаг 2
Табл. 2.16. Снижение размера матрицы
|
Б |
В |
Г |
Д |
Б |
|
3 |
13 |
|
В |
8 |
|
20 |
15 |
А |
8 |
|
|
5 |
Д |
|
10 |
7 |
|
Табл. 2.17. Зануление
|
Б |
В |
Г |
Д |
Б |
|
3 |
6 |
|
В |
0 |
|
5 |
7 |
А |
8 |
|
|
5 |
Д |
|
10 |
0 |
|
Общий размер вычитаний: 7+8=15
Табл. 2.18. Расчет оценок клеток
|
Б |
В |
Г |
Д |
Б |
|
3 |
6 |
|
В |
|
|
5 |
7 |
А |
8 |
|
|
5 |
Д |
|
10 |
|
|
Шаг 3.
Табл.2.19. Снижение размера матрицы
|
Б |
Г |
Д |
Б |
|
6 |
|
В |
|
5 |
7 |
Д |
|
|
|
Зануление невозможно!
Табл. 2.20. Расчет оценок
|
Б |
Г |
Д |
Б |
|
6 |
|
В |
|
5 |
7 |
Д |
|
|
|
Шаг 4.
Табл.2.21. Снижение размера матрицы
|
Б |
Г |
Д |
|
|
В |
|
5 |
Остались два незапрещенных ребра: Д-Г и В-Б
Шаг 5. Составление дерева ветвления алгоритма
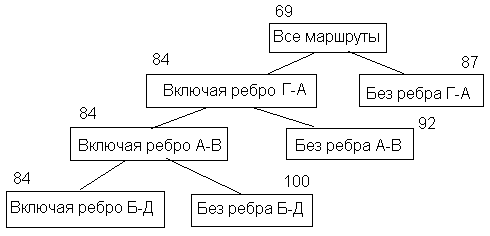
Рис. 2.4. Дерево ветвления алгоритма
Построение оптимального маршрута выполним, используя рис. 2.4. На последнем шаге остались два свободных не запрещенных ребра Д-Г и В-Б. Оба ребра включаем в маршрут и добавляем ребра из левой ветви дерева.
Оптимальный
маршрут будет состоять из ребер Г-А;
А-В; Б-Г; Д-Г и В-Б. После упорядочения
получим:
.
Ответ: Наилучшее время – 84. порядок обхода операций: