1.3.Постановка задачи

Классическая постановка задачи о коммивояжере выглядит следующим образом:

Имеется N городов, которые должен обойти коммивояжер с минимальными затратами. При этом на его маршрут накладывается два ограничения:

• маршрут должен быть замкнутым, то есть коммивояжер должен вернуться в тот город, из которого он начал движение;

• в каждом из городов коммивояжер должен побывать точно один раз, то есть надо обязательно обойти все города, при этом не побывав ни в одном городе дважды.

Для расчета затрат существует матрица условий (Рис. 1.8), содержащая затраты на переход из каждого города в каждый, при этом считается, что можно перейти из любого города в любой, кроме того же самого (в матрице как бы вычеркивается диагональ). Целью решения является нахождения маршрута, удовлетворяющего всем условиям и при этом имеющего минимальную сумму затрат.

Рис. 1.8

1.4. Формулировка задачи на графе

Задача коммивояжера может быть сформулирована как задача на графе в следующей последовательности: построить граф G(X,A), вершины которого соответствуют городам в зоне коммивояжера, а дуги отображают коммуникации, соединяющие пары городов (рис.). Пусть длина a(x,y)>=0 каждой дуги (x,y), принадлежащей А, равна расстоянию, стоимости или времени. Контур, включающий каждую вершину графа G хотя бы один раз, называется маршрутом коммивояжера. Контур, включающий каждую вершину графа G ровно один раз, называется гамильтоновым контуром (по имени ирландского математика Вильяма Роуана Гамильтона, который в 1859 г. первым начал изучение этих задач).

Общей задачей коммивояжера называется задача поиска маршрута наименьшей общей длинны.

Если городам поставить в соответствие вершины графа (рис. 1.9), а соединяющим их дорогам дуги, то в терминах теории графов задача заключается в определении гамильтонова контура минимальной длины.

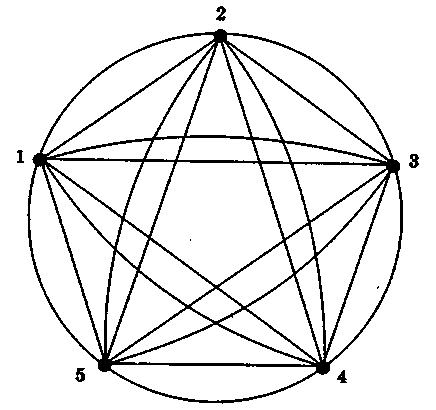
Рис.1.9 Неориентированный граф задачи коммивояжера

Наиболее очевидный способ решения подобных задач – это полный перебор всех вариантов. Однако этот способ наименее удачен, поскольку все интересные с практической точки зрения ситуации возникают именно тогда, когда число возможных вариантов чрезмерно велико. Полный перебор всех вариантов потребовал бы столь большого времени, что стал бы практически нереализуем даже на самых быстродействующих ЭВМ.

К счастью, для многих важных задач дискретной оптимизации существуют методы решения, намного более экономичные, чем полный перебор. Именно такие задачи и алгоритмы будут рассмотрены в данной курсовой работе.

1.5. Этапы решение задачи о почтальоне.

Разобьем процесс принятия решения на этапы:

• Замысел. Наши знания в области математического моделирования позволяют полагать: некоторые из процессов организации производства можно оптимизировать, не внося существенных изменений в структуру предприятия. И это возможно сделать, решая ЗК для оптимизируемого процесса.

• Сбор информации. Знания информационных технологий, позволяет воспользоваться всеми доступными средствами предоставления информации. Мы идем в нужную библиотеку, берем нужные первичные или вторичные источники информации, “заходим” в Интернет и также получаем доступ к вторичным источникам информации. Таким образом, имеем полную картину последних достижений в области методов решения ЗК и программных продуктов по этим алгоритмам. Теперь производим систематизацию данных.

• Анализ ситуации, диагноз и прогноз.

Из всего вышесказанного можно выбрать несколько вариантов поведения:

А. Выбрать и купить готовый программный продукт, внедрить его на производстве, обучить персонал его использованию.

Плюсы: Оперативное решение поставленной задачи.

В случае ошибок в программном обеспечении возможно получение компенсации (в случае грамотно составленного договора).

Минусы: Большие расходы средств компании.

Неизбежность разглашения деловых процессов компании.

Возможно неполное решение поставленной цели, в узких рамках предложенного программного продукта.

Б. Сделать программное обеспечение силами компании.

Плюсы: Управление процессом разработки. Легкость изменения и модернизации. Относительная конфиденциальность.

Минусы: Время написания программного обеспечения может затянуться на неопределенный срок. Возможно, понадобится дополнительно набрать высококвалифицированных специалистов.

За ошибки программного обеспечения придется расплачиваться компании.

В. Оставить все как есть.

Плюсы: Полное отсутствие расходов.

Минусы: Потеря времени на расчеты (для сохранения позиции на рынке нужно затрачивать ресурсы на дополнительный персонал).

Человеческий фактор (большая вероятность ошибки в расчетах людей, чем специализированного программного обеспечения).

Невозможность проконтролировать результаты расчетов в текущем времени. Нет возможности оперативно изменять решение.

Итак, мы решаем следовать варианту Б и решить данную задачу своими силами.