5. Метод Эйлера

1) Найдем постоянную времени , аппроксимируя рабочий участок АВ одним отрезком прямой.

Эквивалентная индуктивность в этом случае составляет величину

Гн,

эквивалентное активное сопротивление схемы (рис.5.40)

Ом,

постоянная времени

с.

Предполагаем, что длительность переходного процесса составляет .

2) Производная по времени в уравнении (5.3) заменяется отношением конечных приращений:

,

и уравнение (5.3) преобразуется к виду: .

Приращение времени фиксируется и связывается с предполагаемой длительностью переходного процесса и количеством шагов N:

.

Пусть , тогда с.

Потокосцепление на -ом шаге находят из найденных на предыдущем (k-ом) шаге значениях потокосцепления и тока. Алгоритм расчета выглядит следующим образом:

. (5.12)

соответствует начальным условиям задачи ( ), Вб, А.

– первый шаг с. В соответствии с выражением (5.12) имеем: Вб. Далее по вебер-амперной характеристике находим ток, соответствующий этому значению потокосцепления А.

– второй шаг с. В соответствии с выражением (5.12) имеем: Вб. Далее по вебер-амперной характеристике находим ток, соответствующий этому значению потокосцепления А.

Аналогичным образом совершаем остальные шаги.

По результатам расчетов строим зависимость . На рис. 5.43 показан начальный участок этой зависимости.

Рис.5.43

Из сопоставления рис.5.42 и 5.43 видно заметное различие зависимостей, найденных двумя способами, что объясняется значительной погрешностью метода Эйлера, связанных с величиной временного шага и графическим определением тока.

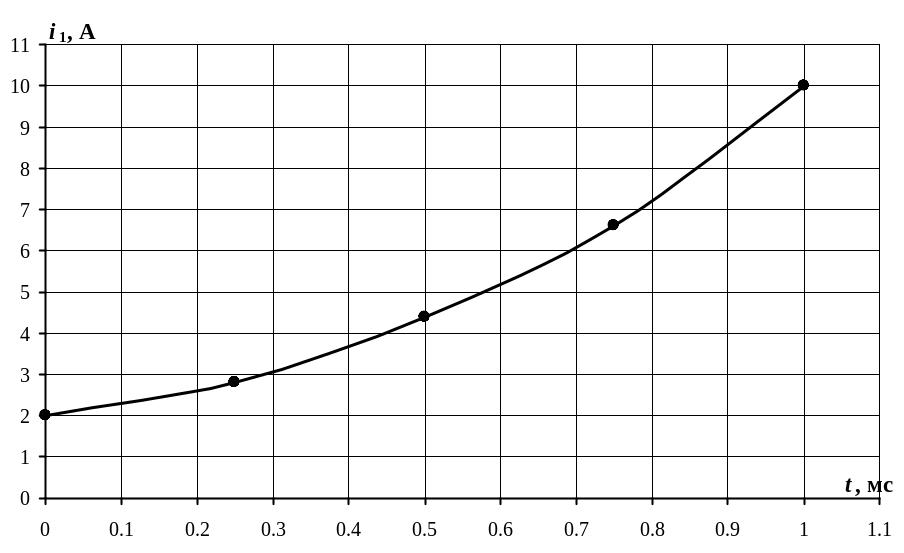
Пример расчета №2 «Расчет переходного процесса в цепи, содержащей нелинейный конденсатор»

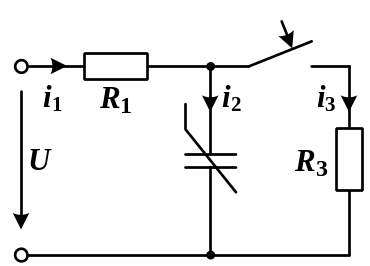
Схема цепи показана на рис. 5.44.

	Данные для расчета: В, Ом, Ом, Ом. Кулон-вольтная характеристика представлена на рис.5.38.
Рис. 5.44

1. – момент коммутации.

2. Для составим систему уравнений, используя законы Кирхгофа:

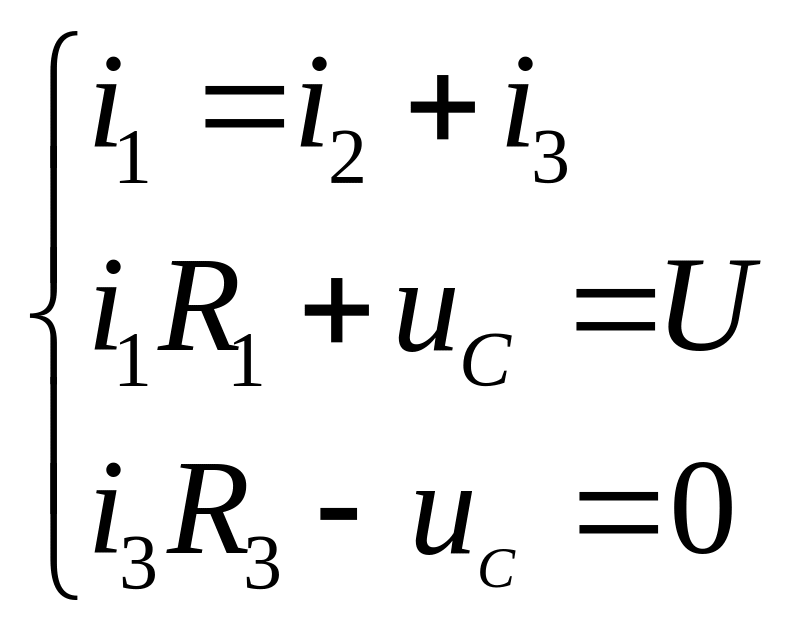. (5.13)

При этом ток через нелинейный конденсатор определяется выражением

.

Преобразуем данную систему к одному дифференциальному уравнению, в котором фигурируют только те переменные, которые описывают характеристику нелинейного элемента – для данной задачи заряд конденсатора q и напряжение на конденсаторе . Для того, чтобы исключить переменные и из системы (5.13), достаточно выразить их из второго и третьего уравнений и далее подставить соответствующие выражения в первое уравнение системы. В итоге получим требуемое дифференциальное уравнение:

.

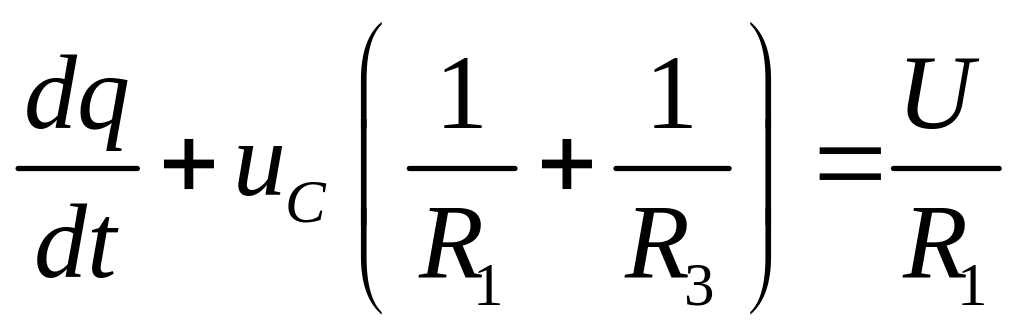Подставляя численные значения параметров, получим расчетное уравнение

. (5.14)

Дифференциальное уравнение (5.14) является нелинейным, так как нелинейной является зависимость .

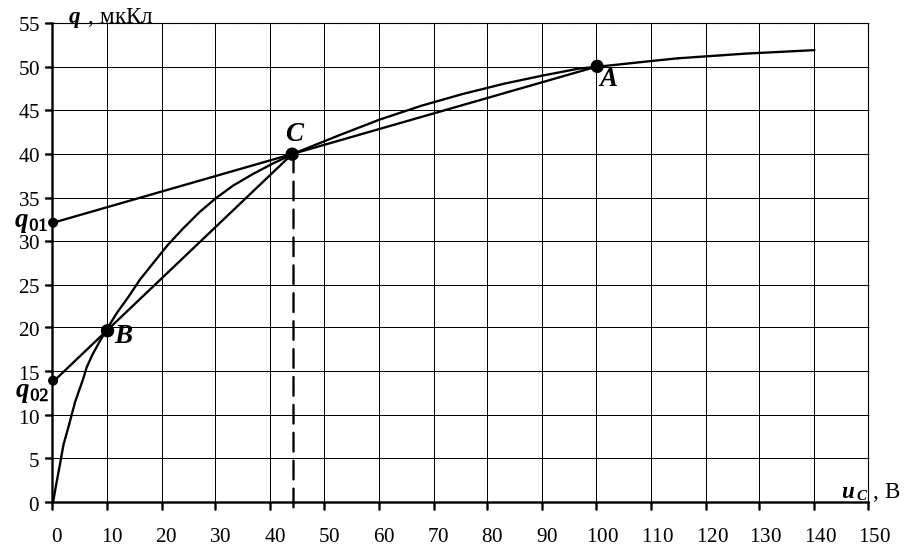
3. Определим рабочий участок на кулон-вольтной характеристике.

3.1. Рассмотрим установившийся режим до коммутации ( ).

Так как постоянный ток через конденсатор не протекает, напряжение на конденсаторе будет равно приложенному:

В

и далее по вебер-амперной характеристике находим Кл.

Таким образом, мы нашли координаты начала рабочего участка – точки А (рис. 5.45).

3.2. Найдем напряжение на конденсаторе в установившемся режиме после коммутации ( ).

Поскольку в этом режиме в цепи действует источник постоянного напряжения, в уравнении (5.14) следует положить , тогда В. Найденное напряжение определяет конец рабочего участка – точку В на рис.5.45.

Рис.5.45