
- •Методичнi рекомендації
- •Глосарій.
- •4. Ромб
- •7. Трапеція
- •Відрізки зображаються відрізками;
- •Паралельні відрізки зображаються паралельними відрізками або відрізками однієї прямої;
- •3) Відношення довжин паралельних відрізків і відрізків однієї прямої зберігається.
- •Глосарій.
- •Глосарій.
- •Теми рефератів для самостійної роботи студентів
МIНIСТЕРСТВО ОСВIТИ І НАУКИ УКРАЇНИ
ДЕРЖАВНИЙ ВИЩИЙ НАВЧАЛЬНИЙ ЗАКЛАД
«КРАСНОДОНСЬКИЙ ПРОМИСЛОВО-ЕКОНОМІЧНИЙ КОЛЕДЖ»
Затверджую заступник
директора з навчальної роботи ________О.Л.Кузьміна „____”
_________2013 р
Розглянуто
та ухвалено на засіданні циклової
комісії гуманітарних і фундаментальних
дисциплін Голова
комісії
______________
Т. О. Матвєєва „____”
_________2013 р Протокол
№_____


Методичнi рекомендації
для самостійного вивчення дисципліни «Вища математика»
для студентів спеціальностей
5.05010201 «Обслуговування комп’ютерних систем і мереж»
5.03050702 «Комерційна діяльність»
5.03050401 «Економіка підприємства»
5.03050901 «Бухгалтерський облік»
Викладач: Приліпа Г.С.
Краснодон 2013
Зміст
Вступ
Теми для самопроробки
Функції, їх графіки та властивості.
Степенева, показникова і логарифмічна функції.
Рівняння, нерівності, системи.
Тригонометричні функції.
Похідна та її застосування.
Інтеграл та його застосування. Елементи теорії ймовірностей та математичної статистики.
Систематизація та узагальнення фактів і методів планіметрії. Паралельність та перпендикулярність прямих і площин у просторі.
Вектори і координати. Многогранники. Об’єми та площі поверхонь многогранників.
Тіла обертання. Об’єми та площі поверхонь тіл обертання.
Теми рефератів для самостійної роботи студентів.
Література.
Вступ
Мета навчання математики у вищих навчальних закладах І-ІІ рівнів акредитації полягає у забезпеченні рівня підготовки студентів з математики, необхідного для спеціальної підготовки та майбутньої професійної діяльності.
Змістове наповнення дисципліни реалізує компетентнісний підхід до навчання, спрямований на формування системи відповідних знань, навичок, досвіду, здібностей і ставлення (відношення), яке дає змогу обґрунтовано судити про застосування математики в реальному житті.
Курс “ Математика” повинен, перш за все, розвивати, поглиблювати, розширювати деякі теми i питання, що вивчалися в основному курсі.
Курс математики, що призначений для спеціальностей «Обслуговування комп'ютерних та інтелектуальних систем і мереж», «Економіка підприємства», «Комерційна діяльність», «Бухгалтерський облік» забезпечуючи гармонійний розвиток образного і логічного мислення, повинен особливу увагу приділити ролі математики в розвитку суспільства та в окремих сферах її застосувань. Зокрема це означає, що студенти повинні оволодіти навиками математичного моделювання. Саме цей вид діяльності повинен бути головним у навчанні майбутніх інженерів та техніків. Досягти цього можна за рахунок зваженого компромісу між строгістю, доступністю та прикладною спрямованістю викладання.
Мета самостійного вивчення - виробити навички математичного дослідження прикладних задач, прищепити студентам уміння самостійно вивчати навчальну літературу з математики та її прикладних питань.
Вимоги до навчальних досягнень студентів орієнтують на результати навчання, які також є об’єктом контролю та оцінювання.
Теми для самопроробки.
ТЕМА №1: Функції, їх графіки та властивості.
Зміст.
Числові функції. Область визначення і множина значень.
Монотонність, парність і непарність функцій. Неперервність функцій.
Література.
Алгебра і початки аналізу: Підруч. Для 10 кл. загальноосвіт. навч. закладів / З. І. Шкіль, З. І. Слєпкань, О. С. Дубинчук: Зодіак-ЕКО, 2003.
Алгебра і початки аналізу: Підруч. Для 11 кл. загальноосвіт. навч. закладів / З. І. Шкіль, З. І. Слєпкань, О. С. Дубинчук: Зодіак-ЕКО, 2003.
Математика: Підруч. для 10 кл. загальноосвіт. навч. закладів / М. І. Бурда, Т. В. Колесник, Ю. І. Мальований, Н. А. Тарасенкова: Київ «Зодіак-ЕКО» 2010.
Алгебра і початки аналізу: : Підруч. для 10 кл. загальноосвіт. навч. закладів / Є. П. Нелін: Харків «Гімназія» 2010.
Алгебра і початки аналізу: : Підруч. для 10 кл. загальноосвіт. навч. закладів / А. Г. Мерзляк, Д. А Номіровський, В. Б. Полонський, М. С. Якір: Харків «Гімназія» 2010.
Завдання для перевірки якості засвоєння знань.
1. Знайти область визначення кожної з функцій:
1,
16)
 ;
2,
17)
;
2,
17)
 ;
3,
18)
;
3,
18)
 ;
;
4,
19)
 ; 5,
20)
; 5,
20)
 ;
6,
21)
;
6,
21)
 ;
;
7,
22)
 ;
8,23)
;
8,23)
 ;
9,
24)
;
9,
24)
 .
.
10,
25)
 ;
11,
26)
;
11,
26)
 ;
12, 27)
;
12, 27)
 ;
;
13,
28)
 ; 14,
29)
; 14,
29)
 ;
15, 30)
;
15, 30)
 .
.
2.Знайти область значень функції:
1)
f(х)
= x2; 2)
f(х)
=
х2
–
2;
3)
f(х)
=
x2
+
4; 4)
f(х)
=
 ;
;
5)
f(х)
=
–
2; 6)
f(х)
=
+
3;
7)
f(х)
=
 ; 8)
f(х)
=
|
x
|
–
4;
; 8)
f(х)
=
|
x
|
–
4;
9)
f(х)
=
|
x
|
+ l;
10)
f(x)=
x2
+
2x;
11)
f(x)
=
 –
2; 12) f(х)
=
–
2; 12) f(х)
=
 .
.
13)
f(х)
=
x2
–
4;
14)
f(х)
=
+
2;
15)
f(х)
=
 ;
;
16) f(х) = x2; 17) f(х) = х2 – 2; 18) f(х) = x2 + 4; 19) f(х) = ;
20) f(х) = – 2; 21) f(х) = + 3; 22) f(х) = ; 23) f(х) = | x | – 4;
24) f(х) = | x | + l; 25) f(x)= x2 + 2x; 26) f(x) = – 2; 27) f(х) = .
28) f(х) = x2 – 4; 29) f(х) = + 2; 30) f(х) = .
3. Чи є парною або непарною функція, задана формулою:
1) f(х) = 3 + х; 2) f(х) = x2 – 8; 3) f(х) = 15х11; 4) f(х) = х2 + х;
5)
f(х)
=
4х10
–
8х12; 6)
f(х)
=
7x3
-
x;
7)
 ; 8)
; 8)
 +
1;
+
1;
9)
 ; 10)
; 10)
 ;
11)
f(х)
=
х2
+
2х
–
5;
;
11)
f(х)
=
х2
+
2х
–
5;
12)
 ; 13)
; 13)
 ;
14)
;
14)
 ;
;
15)
 ;
16) f(х)
=
|х
– 3| + |х
+ 3| 17) f(х)
=
7х2
–
2х;
;
16) f(х)
=
|х
– 3| + |х
+ 3| 17) f(х)
=
7х2
–
2х;
18)
 ;
19) f(х)
= 17х4
– 8х12;
20)
;
19) f(х)
= 17х4
– 8х12;
20)
 ;
;
21)
 ;
22)
;
22)
 ;
23) f(х)
= x2
–
4x
– 3;
;
23) f(х)
= x2
–
4x
– 3;
24)
 ;
25) f(х)
= x
|
x
|;
26)
;
25) f(х)
= x
|
x
|;
26)
 ;
;
27) ; 28) + 1; 29) ;
30) .
Глосарій.
Числовою функцією з областю визначення D називається відповідність, при якої кожному числу x з множини D співставляється за деяким правилом число y, що залежить від x.
Множину, що складається з усіх чисел f(x), таких, що x належить області визначення функції f, називають областю значень функції f і позначають E(f).
Функція f називається парної, якщо для будь-якого x з її області визначення f (–x) = f (x)
Функція f називається непарної, якщо для будь-якого x з її області визначення f (–x) = –f (x)
Функція
 зростає
на множині
зростає
на множині
 ,
якщо для будь-яких x1
і x2
з множині
,
таких, що x2
>
x1,
виконується нерівність
,
якщо для будь-яких x1
і x2
з множині
,
таких, що x2
>
x1,
виконується нерівність
 .
.
Функція
спадає
на множині
,
якщо для будь-яких x1
і x2
з множині
,
таких, що x2
>
x1,
виконується нерівність
 .
.
Достатня
ознака зростання функції.
Якщо
 в кожній точці інтервалу I, то функція
зростає на I.
в кожній точці інтервалу I, то функція
зростає на I.
Достатня
ознака спадання функції.
Якщо
 в кожній точці інтервалу I, то функція
спадає на I.
в кожній точці інтервалу I, то функція
спадає на I.
ТЕМА №2: Степенева, показникова і логарифмічна функції.
Зміст.
Степінь із довільним дійсним показником.
Література.
Алгебра і початки аналізу: Підруч. Для 10 кл. загальноосвіт. навч. закладів / З. І. Шкіль, З. І. Слєпкань, О. С. Дубинчук: Зодіак-ЕКО, 2003.
Алгебра і початки аналізу: Підруч. Для 11 кл. загальноосвіт. навч. закладів / З. І. Шкіль, З. І. Слєпкань, О. С. Дубинчук: Зодіак-ЕКО, 2003.
Математика: Підруч. для 10 кл. загальноосвіт. навч. закладів / М. І. Бурда, Т. В. Колесник, Ю. І. Мальований, Н. А. Тарасенкова: Київ «Зодіак-ЕКО» 2010.
Алгебра і початки аналізу: : Підруч. для 10 кл. загальноосвіт. навч. закладів / Є. П. Нелін: Харків «Гімназія» 2010.
Алгебра і початки аналізу: : Підруч. для 10 кл. загальноосвіт. навч. закладів / А. Г. Мерзляк, Д. А Номіровський, В. Б. Полонський, М. С. Якір: Харків «Гімназія» 2010.
Завдання для перевірки якості засвоєння знань.
Завдання №1. Подати вираз у вигляді суми:
1,
17)
 ;
2, 18)
;
2, 18)
 ;
;
3,
19)
 ; 4,
22)
; 4,
22)
 ;
;
5,
21)
 ;
6, 20)
;
6, 20)
 ;
;
7,
23)
 ;
8, 24)
;
8, 24)
 .
.
9,
25)
 ;
10, 26)
;
10, 26)
 ;
;
11,
27)
 ;
12, 28)
;
12, 28)
 ;
;
13,
29)
 ; 14,
30)
; 14,
30)
 ;
;
15)
 ;
16)
;
16)
 .
.
Завдання №2. Спростити вираз:
1,
16)
 ; 2,
17)
; 2,
17)
 ;
;
3,
18)
 ; 4,
19)
; 4,
19)
 ;
;
5,
20)
 ; 6,
21)
; 6,
21)
 ;
;
7,
22) ;
8, 23)
;
8, 23) ;
;
9,
24) ;
10, 25)
;
10, 25) ;
;
11,
26)
 ;
12, 27)
;
12, 27)

 ;
;
13,
28)
 ;
14, 29)
;
14, 29)
 ;
;
15,
30)
 .
.
Завдання №3. Записати степінь з дробовим показником у вигляді кореня:
1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 ;
5)
;
5)
 ;
6)
;
6)
 ;
;
7)
 ;
8)
;
8)
 ;
9)
;
9)
 ;
10)
;
10)
 ;
11)
;
11)
 ;
12)
;
12)
 ;
;
13)
 ;
14)
;
14)
 ;
15)
;
15)
 ;
16)
;
16)
 ;
;
17)
 ;
18)
;
18)
 ;
19)
;
19)
 ;
20)
;
20)
 ;
21)
;
21)
 ;
;
22)
 ;
23)
;
23)
 ;
24)
;
24)
 ;
25)
;
25)
 ;
26)
;
26)
 ;
27)
;
27)
 ;
;
28)
 ;
29)
;
29)
 ;
30)
;
30)
 .
.
Глосарій.
Степенем
 числа а
> 0 з раціональним показником
числа а
> 0 з раціональним показником
 ,
де
m
,
де
m Z,
п
N
(п>1)
називається число
Z,
п
N
(п>1)
називається число
 .
.
Для будь-яких раціональних чисел р і q і будь-яких додатних а і b справедливі рівності:
-
аp · аq = ap +qn;
аp : аq = ap – q ;
(аp)q = аpq ;
(аb)p = apbp;
 .
.
ТЕМА №3: Рівняння, нерівності, системи.
Зміст.
Системи нелінійних рівнянь, їх види, методи їх розв’язання.
Література.
Алгебра і початки аналізу: Підруч. Для 10 кл. загальноосвіт. навч. закладів / З. І. Шкіль, З. І. Слєпкань, О. С. Дубинчук: Зодіак-ЕКО, 2003.
Алгебра і початки аналізу: Підруч. Для 11 кл. загальноосвіт. навч. закладів / З. І. Шкіль, З. І. Слєпкань, О. С. Дубинчук: Зодіак-ЕКО, 2003.
Математика: Підруч. для 10 кл. загальноосвіт. навч. закладів / М. І. Бурда, Т. В. Колесник, Ю. І. Мальований, Н. А. Тарасенкова: Київ «Зодіак-ЕКО» 2010.
Алгебра і початки аналізу: : Підруч. для 10 кл. загальноосвіт. навч. закладів / Є. П. Нелін: Харків «Гімназія» 2010.
Алгебра і початки аналізу: : Підруч. для 10 кл. загальноосвіт. навч. закладів / А. Г. Мерзляк, Д. А Номіровський, В. Б. Полонський, М. С. Якір: Харків «Гімназія» 2010.
Завдання для перевірки якості засвоєння знань.
Завдання №1. Розв’язати систему рівнянь.
№
|
завдання |
№
|
завдання |
№
|
завдання |
1 |
|
9 |
|
17 |
|
2 |
|
10 |
|
18 |
|
3 |
|
11 |
|
19 |
|
4 |
|
12 |
|
20 |
|
5 |
|
13 |
|
21 |
|
6 |
|
14 |
|
22 |
|
7 |
|
15 |
|
23 |
|
8 |
|
16 |
|
24 |
|
|
|
|
|
25 |
|
Глосарій.
Рівнянням називається рівність, який містить перемінні величини і виконується лише при деяких значеннях цих перемінних.
Рівняння першої степені з одним невідомим
Системи двох рівнянь з двома невідомими
1. Виняток одного невідомого. Якщо одне із рівнянь системи дозволено відносно одного із невідомих, то знаходимо це невідоме і підставляємо в друге рівняння. При цьому приходимо до одного рівняння з одним невідомим.
2. Рішення, основних ненегативних дискримінантів
Нехай
кожне рівняння системи рівняння ,
,

являється
квадратною функцією відносно одного
із невідомого, наприклад,
 .
Щоб система мала розв’язок необхідно,
щоб дискримінанти рівнянь були негативні,
так як
.
Щоб система мала розв’язок необхідно,
щоб дискримінанти рівнянь були негативні,
так як


Якщо
система нерівностей має рішення
 ,
а система рівнянь при
має загальний розв’язок
,
а система рівнянь при
має загальний розв’язок
 ,
то система рівнянь має розв’язок
,
то система рівнянь має розв’язок

Методи їх розв’язання:
а) розклад на множники;
б) виключення змінних;
в) алгебраїчне додавання;
г) заміна змінних;
д) системи однорідних рівнянь;
ж) метод введення нових змінних;
з) графічний метод.
ТЕМА №4: Тригонометричні функції.
Зміст.
Гармонічні коливання.
Література.
Алгебра і початки аналізу: : Підруч. для 10 кл. загальноосвіт. навч. закладів / Є. П. Нелін: Харків «Гімназія» 2010.
Алгебра і початки аналізу: : Підруч. для 10 кл. загальноосвіт. навч. закладів / А. Г. Мерзляк, Д. А Номіровський, В. Б. Полонський, М. С. Якір: Харків «Гімназія» 2010.
Питання для перевірки якості засвоєння знань.
Величина, що характеризує стан коливального процесу в якийсь момент часу.
Назвіть коливання, що поширюється в просторі з часом .
Характеристикою коливань є …
Гармонічні коливання деякої фізичної величини х описуються рівнянням…
Назвіть джерело звуку певної частоти .
Як називається найбільше відхилення тіла від положення рівноваги.
Як називається графік гармонічних коливань.
Побудувати графік функції y = 3 sin (2x + 2π/3).
Побудувати графік функції y = -2sin(0,5x + π/6)
Глосарій.
Коливаннями називаються рухи або процеси, які характеризуються певною повторюваністю в часі.
Гармонічні
коливання деякої фізичної величини х
описуються таким рівнянням де А-
максимальне
значення коливної величини x,
яке називається амплітудою
коливань;
де А-
максимальне
значення коливної величини x,
яке називається амплітудою
коливань;
 -
колова, або циклічна частота; φ - початкова
фаза коливань для моменту часу t
= 0;
-
колова, або циклічна частота; φ - початкова
фаза коливань для моменту часу t
= 0;
 -
фаза коливань для довільного моменту
часу t.
-
фаза коливань для довільного моменту
часу t.
Графік гармонічних коливань – косинусоїда (або синусоїда).
Коливання будуть вільними якщо вони відбуваються за рахунок деякої енергії, переданої коливальній системі в початковий момент часу, при відсутності в наступні моменти часу будь-яких зовнішніх впливів на цю систему.
Певні стани системи в процесі гармонічних коливань повторюються
через
однаковий проміжок часу Т,
який
називається
періодом
коливань
Величина,
обернена до періоду коливань
 виконана коливною системою за одиницю
часу, називається частотою
коливань.
виконана коливною системою за одиницю
часу, називається частотою
коливань.
ТЕМА №5: Похідна та її застосування.
Зміст.
Ознаки сталості, зростання й спадання функції. Екстремуми функції.
Побудова графіків функцій з застосуванням похідної.
Література.
Алгебра і початки аналізу: Підруч. Для 10 кл. загальноосвіт. навч. закладів / З. І. Шкіль, З. І. Слєпкань, О. С. Дубинчук: Зодіак-ЕКО, 2003.
Математика: Підруч. для 10 кл. загальноосвіт. навч. закладів / М. І. Бурда, Т. В. Колесник, Ю. І. Мальований, Н. А. Тарасенкова: Київ «Зодіак-ЕКО» 2010.
Алгебра і початки аналізу: : Підруч. для 10 кл. загальноосвіт. навч. закладів / Є. П. Нелін: Харків «Гімназія» 2010.
Алгебра і початки аналізу: : Підруч. для 10 кл. загальноосвіт. навч. закладів / А. Г. Мерзляк, Д. А Номіровський, В. Б. Полонський, М. С. Якір: Харків «Гімназія» 2010.
Завдання для перевірки якості засвоєння знань.
Завдання №1. Знайти інтервали монотонності функції та її екстремуми.
1).  2).
2). 
3).  4).
4). 
5).  6).
6). 
7).  8).
8). 
9).  10).
10). 
11).  12).
12). 
13).  14).
14). 
15). 
Завдання №2. Дослідити функцію та побудувати її графік.
1).  2).
2). 
3).  4).
4). 
5).  6).
6). 
7).  8).
8). 
9).  10).
10). 
11).  12).
12). 
13).  14).
14). 
15). 
Глосарій.
Якщо
функція
 у внутрішній точці
у внутрішній точці
 проміжку
проміжку
 має екстремум, то в цій точці похідна
має екстремум, то в цій точці похідна
 ,
якщо вона існує, дорівнює нулю.
,
якщо вона існує, дорівнює нулю.
Внутрішня
точка
проміжку
називається стаціонарною
точкою функції
,
якщо в цій точці
 .
Стаціонарні точки і точки, в яких похідна
не існує, називаються критичними
точками функції.
.
Стаціонарні точки і точки, в яких похідна
не існує, називаються критичними
точками функції.
Правило дослідження функції на екстремум
Щоб дослідити функцію на екстремум, треба:
1) знайти стаціонарні точки заданої функції, для цього слід розв’язати рівняння , з коренів цього рівняння вибрати тільки дійсні і ті, які є внутрішніми точками існування функції;
2)
знайти точки, в яких похідна
 не існує (функція
в ціх точках існує). Якщо критичних точок
функція
не має, то вона не має й екстремальних
точок. Така функція не має екстремуму.
Якщо критичні точки є, то їх треба
досліджувати далі, для чого:
не існує (функція
в ціх точках існує). Якщо критичних точок
функція
не має, то вона не має й екстремальних
точок. Така функція не має екстремуму.
Якщо критичні точки є, то їх треба
досліджувати далі, для чого:
3) у кожній критичній точці перевірити зміну знака похідної першого порядку.
Якщо при переході через критичну точку (зліва направо) змінює знак з + на –, то ця точка є точкою максимуму. Якщо змінює знак з – на +, то ця критична точка є точкою мінімуму.
Якщо при переході через критичну точку знак похідної не змінюється, то розглядувана критична точка не є екстремальною точкою заданою функції.
Загальна схема дослідження функції та побудова її графіка
Перш ніж побудувати графік функції, треба провести дослідження функції, а саме:
1. Знайти область існування функції.
2. Знайти точки перетину графіка з координатними осями, інтервали знакосталості функції.
3. Дослідити функцію на періодичність, парність і непарність.
4. Дослідити функцію за допомогою першої похідної (екстремуми функції та інтервали монотонності).
5. На основі проведеного дослідження заповнити таблицю (не обов’язково) та побудувати графік функції.
ТЕМА №6: Інтеграл та його застосування.
Елементи теорії ймовірностей та математичної статистики.
Зміст.
Операції над подіями. Ймовірності суми та добутку подій.
Математичне сподівання дискретної випадкової величини.
Література.
Алгебра і початки аналізу: Підруч. Для 10 кл. загальноосвіт. навч. закладів / З. І. Шкіль, З. І. Слєпкань, О. С. Дубинчук: Зодіак-ЕКО, 2003.
Алгебра і початки аналізу: Підруч. Для 11 кл. загальноосвіт. навч. закладів / З. І. Шкіль, З. І. Слєпкань, О. С. Дубинчук: Зодіак-ЕКО, 2003.
Математика: Підруч. для 10 кл. загальноосвіт. навч. закладів / М. І. Бурда, Т. В. Колесник, Ю. І. Мальований, Н. А. Тарасенкова: Київ «Зодіак-ЕКО» 2010.
Алгебра і початки аналізу: : Підруч. для 10 кл. загальноосвіт. навч. закладів / Є. П. Нелін: Харків «Гімназія» 2010.
Алгебра і початки аналізу: : Підруч. для 10 кл. загальноосвіт. навч. закладів / А. Г. Мерзляк, Д. А Номіровський, В. Б. Полонський, М. С. Якір: Харків «Гімназія» 2010.
Завдання для перевірки якості засвоєння знань.
Завдання №1.
Задача
1.
В урні
 білих і
білих і
 чорних куль. З урни виймають навмання
одну кулю. Знайти ймовірність того, що
ця куля - біла.
чорних куль. З урни виймають навмання
одну кулю. Знайти ймовірність того, що
ця куля - біла.
Задача 2. Кинуто дві гральні кістки. Знайти ймовірність того, що сума очок на гранях, що випали , дорівнює семи.
Задача 3. Кинуто дві гральні кістки. Знайти ймовірність того, що сума очок на гранях, що випали , дорівнює п'яти, а добуток - чотирьом.
Задача 4. Монета кинута три рази. Знайти ймовірність того, що хоча б один раз з'явився герб.
Задача 5. У коробці міститься 6 однакових занумерованих кубиків. Навмання по одному витягають усі кубики з коробки. Знайти ймовірність того, що номера витягнутих кубиків з'являться в зростаючому порядку.
Задача 6. Повна колода карт (52 листа) ділиться навмання на дві рівні пачки по 26 листів. Знайти ймовірність того, що в кожній із пачок виявиться по два туза.
Задача 7. Повна колода карт (52 листа) ділиться навмання на дві рівні пачки по 26 листів. Знайти ймовірність того, що в однієї з пачок не буде жодного туза, а в інший - усі чотири.
Задача 8. У шухляді є 15 деталей, серед котрих 10 пофарбованих. Складальник навмання витягає 3 деталі. Знайти ймовірність того, що витягнуті деталі виявляться пофарбованими.
Задача 9. У групі 12 студентів, серед котрих 8 відмінників. За списком навмання відібрані 9 студентів. Знайти ймовірність того, що серед відібраних студентів виявляться 5 відмінників.
Задача 10. Набираючи номер телефону, абонент забув останні три цифри і, пам'ятаючи лише, що цифри різноманітні, набрав їх навмання. Знайти ймовірність того, що набрані потрібні цифри.
Задача 11. На стелажі бібліотеки у випадковому порядку стоять 15 підручників, причому 5 із них у плетінні. Бібліотекар бере навмання 3 підручник. Знайти ймовірність того, що хоча б один з узятих підручників виявиться в плетінні.
Задача 12. Для сигналізації про аварію встановлені два незалежно працюючі сигналізатори. Ймовірність того, що при аварії сигналізатор спрацює, дорівнює 0,95 для першого і 0,9 для другого сигналізатора. Знайти ймовірність того, що при аварії спрацює тільки один сигналізатор.
Задача 13. Два стрілки стріляють по мішені. Ймовірність влучення в мішень при однім пострілі для першого стрілка дорівнює 0,7, а для другого - 0,8. Знайти ймовірність того, що при однім залпі в мішень потрапляє тільки один зі стрілків.
Задача 14. Ймовірність одного влучення в ціль при однім залпі з двох гармат дорівнює 0,38. Знайти ймовірність поразки цілі при однім пострілі першою гарматою, якщо відомо, що для другої гармати ця ймовірність дорівнює 0,8.
Задача 15. Відділ технічного контролю перевіряє вироби на стандартність. Ймовірність того, що виріб стандартний, дорівнює 0,8. Знайти ймовірність того, що з двох перевірених виробів тільки один стандартний.
Задача 16. Студент знає 20 із 25 питань програми. Знайти ймовірність того, що студент знає запропоновані йому екзаменатором три питання.
Задача 17. У шухляді міститься 10 однакових кубиків з номерами від 1 до 10. Навмання витягають по одному 3 кубика. Знайти ймовірність того, що послідовно з'являться кубики з номерами 1, 2, 3, якщо кубики витягаються без повернення.
Задача 18. Для руйнації моста достатньо влучення однієї авіаційної бомби. Знайти ймовірність того, що міст буде зруйнований, якщо на нього впадуть 4 бомби з ймовірностями влучення, відповідно рівними 0,3; 0,4; 0,6; 0,7.
Задача 19. Ймовірність хоча б одного влучення в мішень стрілком при трьох пострілах дорівнює 0,875. Знайти ймовірність улучення при однім пострілі.
Задача 20. Ймовірність хоча б одного влучення в ціль при чотирьох пострілах дорівнює 0,9984. Знайти ймовірність влучення в ціль при однім пострілі.
Задача 21. Прилад може працювати в двох режимах: 1) нормальному і 2) ненормальному. Нормальний режим спостерігається в 80% випадках роботи приладу; ненормальний - у 20%. Ймовірність виходу приладу з ладу за час t у нормальному режимі дорівнює 0,1; у ненормальному - 0,7. Знайти повну ймовірність виходу приладу з ладу за час t.
Задача 22. У шухляді міститься 12 деталей заводу №1, 20 деталей заводу №2, 18 деталей заводу №3. Ймовірність того, що деталь заводу №1 відмінної якості, дорівнює 0,9; для заводів №2 і №3 ці ймовірності відповідно рівні 0,6 і 0,9. Знайти ймовірність того, що витягнута навмання деталь виявиться відмінної якості.
Задача 23. У першій урні міститься 10 куль, із них 8 білих; у другій урні 20 куль, із них 4 білих. З кожної урни навмання витягли по одній кулі, а потім із цих двох куль навмання узята одна куля. Знайти ймовірність того, що узята біла куля.
Задача
24.
Є дві урни: у перший
білих куль і
чорних; у другій
 білих і
білих і
 чорних. З першої урни в другу переміщають
одну кулю; кулі перемішуються, і потім
із другої урни в першу переміщають одну
кулю. Після цього з першої урни беруть
навмання одну кулю. Знайти ймовірність
того, що вона буде білою.
чорних. З першої урни в другу переміщають
одну кулю; кулі перемішуються, і потім
із другої урни в першу переміщають одну
кулю. Після цього з першої урни беруть
навмання одну кулю. Знайти ймовірність
того, що вона буде білою.
Задача 25. Група студентів складається з відмінників, з , що добре встигають, і з , що займаються слабко. Відмінники на майбутньому іспиті можуть одержати тільки відмінно. Добре встигаючі студенти можуть одержати з рівною ймовірністю добре і відмінно. Ті, що займаються слабко, можуть одержати з рівною ймовірністю добре, задовільно і незадовільно. Для здавання іспиту викликається навмання один студент. Знайти ймовірність того, що він одержить добре або відмінно.
Глосарій.
Означення. Статистична ймовірність приблизно дорівнює відносній частоті (або числу, близькому до неї) при достатньо великому числі випробувань.
Теорема додавання ймовірностей. Ймовірність появи хоча б однієї з двох подій дорівнює сумі ймовірностей цих подій без ймовірності їх добутку:
 .
.
У випадку несумісних подій ця рівність набуває вигляд:
 .
.
Означення.
Ймовірністю події
 за умови, що наступила подія
за умови, що наступила подія
 (умовною ймовірністю), називається число
(умовною ймовірністю), називається число
 ,
,
 .
.
Теорема множення ймовірностей. Ймовірність спільної появи двох подій дорівнює добутку ймовірності однієї з них на умовну ймовірність іншої, обчислену в припущенні, що перша подія відбулася:
 .
.
формулу Байєса:
 ,
,
 ,
,
де
знаменник
 є повна ймовірність.
є повна ймовірність.
Означення.
Повторення
незалежних щодо події
 випробувань, у кожному з яких ймовірність
появи події
однакова, називають схемою
Бернулі.
випробувань, у кожному з яких ймовірність
появи події
однакова, називають схемою
Бернулі.
ТЕМА №7: Систематизація та узагальнення фактів і методів планіметрії.
Паралельність та перпендикулярність прямих і площин у просторі.
Зміст.
Аксіоми планіметрії. Система опорних фактів курсу планіметрії.
Геометричні і аналітичні методи розв’язування планіметричних задач
Паралельність прямих і площин у просторі. Основні поняття, аксіоми стереометрії і найпростіші наслідки із них.
Взаємне розміщення прямих у просторі. Паралельне проектування і його властивості.
Зображення фігур у стереометрії. Паралельність прямої і площини. Паралельність площин.
Література.
Алгебра і початки аналізу: Підруч. Для 11 кл. загальноосвіт. навч. закладів / З. І. Шкіль, З. І. Слєпкань, О. С. Дубинчук: Зодіак-ЕКО, 2003.
Погорєлов О.В. Геометрія: Планіметрія: Підруч. для 10-11 кл. загальноосвіт. навч. закл.– К.: Школяр, 2004, Освіта, 2001
Математика: Підруч. для 10 кл. загальноосвіт. навч. закладів / М. І. Бурда, Т. В. Колесник, Ю. І. Мальований, Н. А. Тарасенкова: Київ «Зодіак-ЕКО» 2010.
Завдання для перевірки якості засвоєння знань.
Завдання №1.
1.16Знайти площу трикутника, медіани якого рівні 12, 15 й 21.
2.17
Біля окружності описана равнобока
трапеція. Радіус цієї окружності в
 раз менше радіуса окружності, описаної
біля трапеції. Знайти кут при підставі
трапеції.
раз менше радіуса окружності, описаної
біля трапеції. Знайти кут при підставі
трапеції.
3.18
Визначити площа рівнобедреного
трикутника, якщо довжина його підстави
дорівнює
 ,
а висота, опущена на бічну сторону,
дорівнює
,
а висота, опущена на бічну сторону,
дорівнює
 .
.
4. 19 У рівнобедреному трикутнику бічна сторона дорівнює 20, підстава дорівнює 24. Знайти відстань між крапкою перетинання медіан і крапкою перетинання бісектрис цього трикутника.
5.20
Бісектриса прямого кута розділила
гіпотенузу на відрізки, рівні
 й
й
 .
Знайти площу трикутника.
.
Знайти площу трикутника.
6.21
Радіуси вписаної й описаної окружності
прямокутного трикутника відповідно
рівні 2 див й 5 див. Знайти катети
трикутника» якщо відстань між центрами
окружностей дорівнює
 .
.
7.22
Біля кола описана трапеція, бічні
сторони якої утворять із більшої з
паралельних сторін гострі кути
 й
й
 .
Визначити радіус кола, якщо площа
трапеції
.
Визначити радіус кола, якщо площа
трапеції

8.23
У прямокутному трикутнику гіпотенуза
 ,
а один з гострих кутів дорівнює
.
Визначити радіус уписаного кола.
,
а один з гострих кутів дорівнює
.
Визначити радіус уписаного кола.
9.
Катети прямокутного трикутника рівні
 й
.
Знайти довжину бісектриси прямого кута.
й
.
Знайти довжину бісектриси прямого кута.
10.24
У равнобочную трапецію вписане коло.
Одна з бічних сторін її ділиться крапкою
торкання на відрізки довжиною
 й
й
 .
Визначити площа трапеції.
.
Визначити площа трапеції.
11.25
У равнобочной трапеції, описаної біля
окружності радіуса
 відношення довжин бічної сторони й
більшої підстави є задане число
відношення довжин бічної сторони й
більшої підстави є задане число
 .
Знайдіть довжин меншої підстави.
.
Знайдіть довжин меншої підстави.
12.26 У равнобочной трапеції лежать дві дотичні окружності з радіусами , кожна з яких стосується обох підстав й однієї з бічних сторін, а центри окружностей лежать на діагоналях. Знайдіть сторони трапеції.
13.27 Окружності радіусами 8 й 3 стосуються внутрішнім образом. Із центра більшої окружності проведені дотичні до меншої окружності. Знайти довжину дотичної.
14.28Три окружності радіуса попарно зовнішнім образом стосуються один одного. Обчислити площу криволінійного трикутника, обмеженого цими окружностями.
15.29 На сторону ВР ромба АВСД опущена висота ДК. Діагональ АС перетинає висоту ДК у крапці М так, що ДМ:МК = 13:7. Знайдіть ДК, якщо відомо, що АК=17.
Завдання №2 Для перевірки якості засвоєння знань студенту необхідно скласти тест.
І варіант
1. Площина і пряма, яка не лежать на ній
А |
Б |
В |
Г |
Д |
не перетинаються |
перетинаються в одній точці |
або не перетинаються, або перетинаються в одній точці |
розташовані перпендикулярно |
Інша відповідь |
2. Скільки площин можна провести через пряму а і точку В, яка не належить прямій а?
А |
Б |
В |
Г |
Д |
одну |
дві |
Три |
безліч |
інша відповідь |
3. Якщо три вершини прямокутника лежать у деякій площині, то четверта його вершина лежить
А |
Б |
В |
Г |
Д |
поза цією площиною |
у цій же площині |
в точці перетину діагоналей |
в площині перпендикулярній до даної |
інша відповідь |
5. Точка М не лежить в площині трикутника АВС. Як розміщені прямі МА і ВС?
А |
Б |
В |
Г |
Д |
мимобіжні |
перпендикулярно |
паралельно |
перетинаються |
інша відповідь |
6. Площина , яка паралельна стороні трикутника АВС, перетинає сторони ВА і ВС відповідно у точках М і N. Знайти МN, якщо ВМ=4 м, АМ=6 см, АС=8 м.
А |
Б |
В |
Г |
Д |
3,2 м |
4 м |
5 м |
6 м |
інша відповідь |
7. Трикутники АВС і МВС не лежать в одній площині і мають спільну сторону. Точки Д, Н, К – середини сторін МВ, СМ, АС. Відрізок АВ перетинає площину ДНК в точці S. Знайти SК, якщо ВС=8 см.
А |
Б |
В |
Г |
Д |
12 см |
2 см |
16 см |
4 см |
інша відповідь |
8. Точка Р лежить між паралельними площинами і . Прямі m і n, що проходять через точку Р, перетинають площину в точках N1 і М1, а площину - в точках N2 і М2 відповідно. Знайдіть РМ,
якщо N1 Р : N1 N2 = 1:3, М1 М2 = 15 дм.
А |
Б |
В |
Г |
Д |
5 см |
5 дм |
45 дм |
немає розв’язку |
інша відповідь |
ІІ варіант
1. Дві прямі у просторі перетинаються і мають:
А |
Б |
В |
Г |
Д |
більш, ніж одну спільну точку |
дві спільні точки |
одну спільну точку |
безліч спільних точок |
інша відповідь |
2. Скільки площин можна провести через пряму і точку, яка лежить на цій прямій?
-
А
Б
В
Г
Д
одну
дві
три
безліч
інша відповідь
3. Скільки спільних прямих мають дві площини, які перетинаються?
-
А
Б
В
Г
Д
одну
дві
три
безліч
інша відповідь
5. Точка Р не належить площині квадрата АВСД. Як розміщені прямі ВС і РД?
-
А
Б
В
Г
Д
мимобіжні прямі
перпен
дикулярно
паралельно
перетинаються
інша відповідь
6. Через кінець А відрізка АВ проведено площину . Через кінець В і точку К цього відрізка проведено паралельні прямі, які перетинають площину в точках В1 і К1. Знайти довжину відрізка КК1, якщо АК:КВ =3:2 і ВВ1=16 м.
А |
Б |
В |
Г |
Д |
9,6 м |
6,4 м |
26 |
3,2 м |
інша відповідь |
7. Трикутник А SД і трапеція АВСД мають спільну сторону АД і лежать в різних площинах. Через основу ВС трапеції і середину відрізка S Д – точку Н проведено площину, яка перетинає пряму А S в точці К. Знайдіть НК, якщо АД=10 см.
А |
Б |
В |
Г |
Д |
5 см |
10 см |
15 см |
20 см |
інша відповідь |
8. Площини і паралельні. Точки N1 , N2 і М1 , М2 належать цим площинам так, що прямі N1 М1 і N2 М2 перетинаються в точці Р. Обчислити Р N1 і РМ2 , якщо N1 М1 = 6 дм, Р N2 = 25 см, Р М2 : Р N2 = 3.
А |
Б |
В |
Г |
Д |
15 см і 7,5 см |
1,5 дм і 7,5 дм Або 3 дм і 7,5 дм |
3 дм і 7,5 дм |
задача розв’язку немає |
інша відповідь |
ІІІ варіант
1. Як розміщені площина і пряма С, яка паралельна прямій а, якщо площина перпендикулярна до прямої а?
А |
Б |
В |
Г |
Д |
перпендикулярно |
паралельно |
мимобіжні прямі |
перетинаються |
інша відповідь |
2. Діагоналі двох квадратів відповідно паралельні. Чи паралельні відповідні сторони цих квадратів?
А |
Б |
В |
Г |
Д |
так |
ні |
перпендикулярн1 |
мимобіжні |
інша відповідь |
3. Похила дорівнює 2 см. Чому дорівнює проекція похилої на площину, якщо похила утворює з площиною проекції кут 300?
А |
Б |
В |
Г |
Д |
1 |
2 |
|
3 |
інша відповідь |
4. Площа трикутника А1В1С1 дорівнює 42 см. Він є ортогональною проекцією трикутника АВС з сторонами 13 см, 14 см і 15 см. Знайти кут між площинами АВС і А1В1С1.
А |
Б |
В |
Г |
Д |
300 |
450 |
600 |
900 |
інша відповідь |
6. Із точки до площини проведено дві похилі. Знайти довжини похилих, якщо одна з них на 13 см більша від другої, а проекції похилих дорівнюють 6 см і 20 см
А |
Б |
В |
Г |
Д |
6 см і 7 см |
7,5 см і 20,5 см |
3 |
13 см і 26 см |
інша відповідь |
7. Ребро куба АВСДА1В1С1Д1 дорівнює а. Знайти відстань між прямими АА1 і ВД.
А |
Б |
В |
Г |
Д |
|
|
|
|
інша відповідь |
8. Трикутник АВС і КВС правильні і лежать у взаємно перпендикулярних площинах. Знайти відстань від точки К до прямої АС, якщо ВС=2 см
А |
Б |
В |
Г |
Д |
3 см |
1,5 см |
|
5 см |
інша відповідь |
4 варіант
1. Через точку Р проведено прямі паралельні діагоналям даного правильного шестикутника. Чи є на малюнку взаємно перпендикулярні прямі?
А |
Б |
В |
Г |
Д |
так |
ні |
всі прямі паралельні |
всі прямі мимобіжні |
інша відповідь |
2. Скільки можна провести площин перпендикулярних до прямої а через точку А, що належить даній прямій?
А |
Б |
В |
Г |
Д |
одну |
дві |
три |
безліч |
інша відповідь |
3. Похила дорівнює 10 см. Чому дорівнює проекція похилої на площину, якщо похила утворює з площиною проекції кут 450?
А |
Б |
В |
Г |
Д |
10 |
5 см |
5 см |
9 см |
інша відповідь |
4. Площа трикутника А1В1С1 дорівнює 12 см2 . Він є ортогональною проекцією трикутника АВС з сторонами 4 см, 13 см і 15 см. Знайти кут між площинами АВС і А1В1С1.
А |
Б |
В |
Г |
Д |
300 |
450 |
600 |
900 |
інша відповідь |
 5.
Точка Е не належить площині прямокутника
АВСД, ВЕ АВ, ВЕ ВС. Як розміщені
прямі ВЕ і СД?
5.
Точка Е не належить площині прямокутника
АВСД, ВЕ АВ, ВЕ ВС. Як розміщені
прямі ВЕ і СД?
А |
Б |
В |
Г |
Д |
ВЕ ІІ СД |
ВЕ СД |
мимобіжні |
перетинаються
|
інша відповідь |
6. Із точки до площини проведено дві похилі, що дорівнюють 23 см і 33 см. Знайти довжину перпендикуляра до площини, якщо проекції похилих відносяться як 2:3.
А |
Б |
В |
Г |
Д |
10см |
9 см |
5 см |
4,6 см |
інша відповідь |
7. Ребро куба АВСДА1В1С1Д1 дорівнює 9. Знайти відстань між прямимиАС і В1 Д1.
А |
Б |
В |
Г |
Д |
4,5 |
|
|
9 см |
інша відповідь |
8.
Рівносторонній трикутник МВС і
прямокутний трикутник АВС лежать у
взаємно перпендикулярних площинах.
Знайти відстань від точки М до прямої
АС, якщо ВС=4
см,
 АСВ=600.
АСВ=600.
А |
Б |
В |
Г |
Д |
3 см |
15 см |
|
6 см |
інша відповідь |
Завдання №3. Розв’язати задачу, де N-це порядковий номер студента за списком у академічному журналі.
|
|









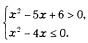
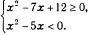













 м
м
 см;
16
см
см;
16
см




 см
см см
см
 75
см
75
см
