Нахождение значений шкалирующих коэффициентов.

Для удобства изложения введем некоторые специальные обозна­чения. Для каждого j-го критерия через w_j обозначим худшее значение и через b_j — лучшее. Тогда для положительно ориенти­рованных шкал будем иметь . Пусть I — множество всех номеров критериев; в нашем примере I={1, 2, 3, 4}. Пусть Т — подмножество множества I, а — его дополнение до I, или =1—Т. Через x^T обозначим профиль, в котором компоненты x_j равны b_j для всех и w_j для Таким образом, если, на­пример, Т ={2, 3}, то

Так как v_j(w_j) =0 и v_j(b_j)=1, то

,

так что когда Т ={2, 3}, то v(х^T) =λ₂+λ₃. Определим также

.

Отметим, что, когда Т является одноэлементным множеством {j}, мы имеем

v(x^{j})=λ_j=λ({j}).

Один из возможных методов для определения λ_j, например, та­кой. Вначале ранжируем профили x^{1}, …, x^{4}. Предположим, например, Вы считаете, что х^{2}>х^{1}>х^{4}>х^{3}. Отсюда сле­дует, что для Вас λ₂>λ₁>λ₄>λ₃. Затем Вы могли бы получить бо­лее тонкие неравенства, сравнивая, скажем, х^{2} и x^{1,3,4}. Если в этой паре х^{2} более предпочтительно, то мы могли бы сделать вывод, что λ₂>0,5.

Заметим, что когда Вас просят сравнить х^т с x^s, то Вам за­дают по существу такой вопрос: «Предположим, что профиль х соответствует наихудшему случаю (w₁, w₂, w₃, w₄) и Вы можете выбрать некоторые w_j, которые будут заменены на лучшие зна­чения. Хотите ли Вы улучшить уровни критериев с номерами из Т или же из S?».

Такой метод анализа позволяет только установить неравен­ства для λ_j. В некоторых специальных случаях могут быть полу­чены точные числовые значения, если имеются равенства некото­рых профилей по предпочтительности. Например, если Вам без­различен выбор между х^{T} и х^{{ }}, т. е. эти два вектора одинако­вы по предпочтительности, то λ(T)=0,5. Но это — специальный случай.

Продолжим разбор случая, когда λ₂>λ₁>λ₄>λ₃. Теперь будем сравнивать два профиля (w₁, x₂, w₃, w₄) и х^{T} и изменять уро­вень х₂, пока не наступит момент безразличия в выборе между ними. Предположим, что это происходит при x₂=350, т. е.

(2,0; 350; 0,15; 12,0) ~ (9,0; 200; 0,15; 13,50).

Тогда мы имеем

v(2,0; 350; 0,15; 13,50) = v(9,0; 200; 0,15; 13,50)

или

λ₂v₂(350)= λ_1.

А так как предполагается, что компонента v₂ функции ценности уже построена, то мы можем найти v₂(350). Допустим, что v₂(350) =0,6, так что

0,6 λ₂= λ₁. (1)

Таким же образом мы можем определить соотношения между λ₄ и λ₂ и между λ₃ и λ₂. Примем, в частности, что

(2,0; 240; 0,15; 13,50) ~ (2,0; 200; 0,15; 12,00)

и

v₂(240)=0,4,

т. е.

0,4λ₂= λ₄. (2)

а также, что

(2,0; 210; 0,15; 13,50) ~ (2,0; 200; 0,90; 13,50)

и

v₂(210)=0,1,

так что

0,1λ₂= λ₃. (3)

Из (1) —(3) и λ₁+λ₂+λ₃+λ₄=1 мы получаем

λ₁=0,286, λ₂=0,467, λ₃=0,048, λ₄=0,190.

При желании мы можем поставить дополнительные вопросы и на основании полученных ответов составить «переопределенную» систему уравнений (на практике совокупность полученных ответов наверняка окажется противоречивой). Эти противоречия анали­тик может использовать для того, чтобы «побудить» лицо, прини­мающее решение, более внимательно отнестись к своим предпоч­тениям, и может быть, пересмотреть их. Можно надеяться, что причины противоречивости будут найдены, после чего будет уста­новлена непротиворечивая система предпочтений.

Дополнительные замечания о функции λ.

Функция λ, оп­ределенная на подмножествах множества I, обладает обычными свойствами вероятностной меры:

1. λ(T)≥0;

2. λ(I)=1, для ;

3. λ(S U T)= λ(S)+ λ(T), если S и Т не пересекаются.

Таким образом, отыскание функции λ родственно задаче уста­новления подходящего вероятностного распределения на конеч­ном выборочном пространстве. Очень часто при определении ве­совой меры λ, точно так же, как и при нахождении численных значений вероятностной меры, нецелесообразно начинать с опре­деления численных значений на «атомарном» уровне, т. е. в нашем случае е чисел λ₁, λ₂, ... Вместо этого может оказаться удоб­нее вначале установить численные значения для подмножеств (т. е. определить λ(T) для специальных подмножеств), а затем определить условные меры. Рассмотрим, например, случай 10 кри­териев с иерархической структурой, представленной на рис. 3. Положим для этого случая

I={1,2, ..., 10},

A={1},B = {2, 3, 4}, С={5, 6}, D={7, 8, 9, 10},

Е=А U В, F=C U D.

И ерархическая структура целей, используе­мая при нахождении чис­ленных значений шкалирую­щих коэффициентов

В подобном примере с иерархической структурой может оказать­ся более естественно сравнивать

λ(E) с λ(F),

λ(A) с λ(B),

λ(C) с λ(D),

Используя аналогию с теорией вероятностей, определим также

условные весовые функции, как, например, λ(B|E)= λ(B)/ λ(E),

для , где λ(B|E) характеризует «весовую важность множества критериев В в подмножестве Е или условные веса В и Е. При на­личии большого числа критериев и их четко выраженной иерархи­ческой структуры очень важно выделить компоненты задачи я най­ти численные значения условных весов. На рис. 4 представле­ны численные значения условных весов, в данном случае произ­вольно назначенные нами (в действительности эти числовые зна­чения должны быть указаны (назначены) лицом, принимающим решение). Например, мы положили

λ(E)=0,6 и λ(F)=0,4,

λ(A|E)=0,5 и λ(B|E)=0,5

λ({2}|B)=0,5, λ({3}|B)=0,3,

и λ({4}|B)=0,2

λ(C|F)=0,8 и λ(D|F)=0,2,

и т.д.

Укажем теперь, как находится, например, значение λ₃. Чтобы найти λ₃, мы должны произвести умножение

λ₃= λ({3}|B)* λ(B|E)* λ(E).

Таким же образом мы получаем все остальные λ_j, представлен­ные на рис. 4 во второй строке снизу.

И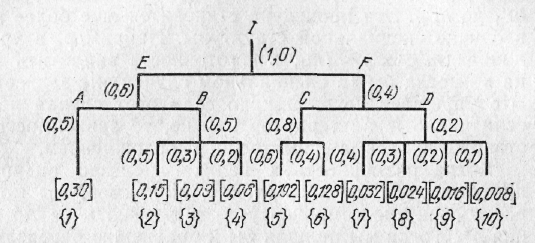 ллю­стративные значе­ния шкалирующих коэффициентов для иерархической структуры на рис.3

В подобной задаче может быть ясно, например, как назначить численные значения условных весов для подмножеств Е и F, но может оказаться трудным распределить веса между Е и F. Одна­ко способность структуризовать часть задачи может позволить произвести анализ чувствительности для тех решающих оценок, которые трудно получить. Это замечание об анализе чувствитель­ности и другие, ему подобные, особенно важны, если в процессе выработки решения участвует не один, а несколько лиц, ответ­ственных за принятие решения.

Задание

• сформировать множество Парето - оптимальных альтернатив;

• построить одномерные функции ценности для оценки альтернатив по каждому из критериев;

• проанализировать связь между критериями используя механизм построения профилей;

• построить многомерную функцию ценности и с ее помощью оценить альтернативы.

Литература

1. Кини Р.Л., Райфа Х. Принятие решений при многих критериях: предпочтение и замещение. М. "Радио и связь", 2006.

2. Методы и алгоритмы принятия решений в примерах и задачах: учебное пособие / М. А. Николаева, О. Ф. Зотова; Уфимск. гос. авиац. техн. ун-т. – Уфа, 2010 – 110 с.