Задание для самостоятельной работы

Вычислить тройные интегралы:

Задача 10. где призма, ограниченная плоскостями

Задача 11. где куб, ограниченный плоскостями

Задача 12. где область V расположена в первом октанте и ограничена конусом и плоскостями

Задача 13. где V – параллелепипед, ограниченный плоскостями

Задача 14. Вычислить трехкратный интеграл и построить область интегрирования

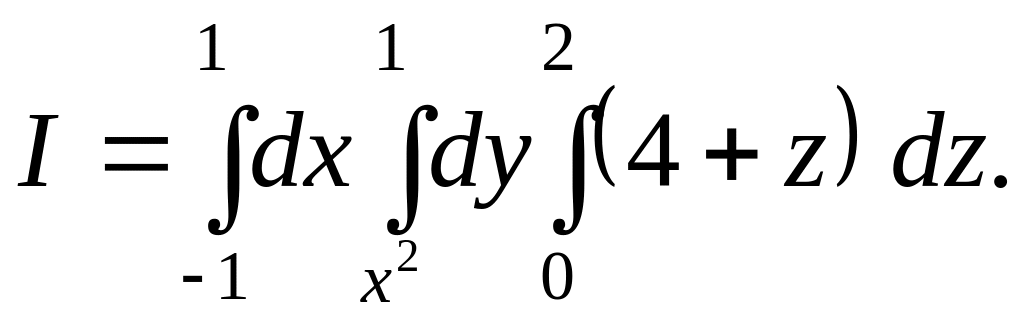
Указание. Вспомним из аналитической геометрии в пространстве, что геометрические образы, соответствующие уравнениям, следующие:

плоскости, параллельные координатной плоскости YOZ, проходящие через точки и

плоскость, параллельная координатной плоскости XOZ, проходящая через точку

параболический цилиндр, симметричный координатной плоскости YOZ, с образующей параллельной оси Oz («корыто», поставленное вертикально открытой частью в сторону положительного направления оси Oy).

координатная плоскость.

плоскость, параллельная плоскости XOY, отсекающая 2 единицы по оси Oz.

Занятие №9. Приложения тройных и криволинейных интегралов

Цель занятия: закрепить знания тройных и криволинейных интегралов на примерах использования их в прикладной математике.

Учебные вопросы

1. Решение геометрических задач с помощью тройных интегралов.

2. Решение физических задач с помощью тройных интегралов.

3. Решение геометрических и физических задач с помощью криволинейных интегралов

Ход занятия

1. Решение геометрических задач с помощью тройных интегралов

Рабочие формулы

Объем пространственной области V:

Решение задач сводится к вычислению тройных интегралов (см. предыдущее занятие).

Задание для самостоятельной работы

Задача 1. Найти объем тела, ограниченного поверхностями:

1)

2)

3)

4)

5)

Указание. 1. Необходимо вспомнить геометрические образы, соответствующие данным уравнением или построить данные поверхности методом сечений.

2. В случае 5) перейти к сферическим координатам.

2. Решение физических задач с помощью тройных интегралов

1. Статистические моменты.

Произведение массы точки на ее расстояние от какой-нибудь оси называется статистическим моментом этой точки относительно оси. Сумма статистических моментов точек называется статистическим моментом системы. Статистические моменты тела с плотностью в каждой точке относительно координатных плоскостей имеет вид:

2) Центр тяжести можно определить как такую точку, что если в ней сосредоточить всю массу системы, то ее статистический момент относительно какой-нибудь оси будет равен соответствующему статистическому моменту всей системы. Координаты центра тяжести определяются по формулам:

где есть масса тела.

3) Масса тела, занимающего объем V с заданной объемной плотностью в точке тела вычисляется по формуле:

4) Моментом инерции материальной точки P с массой M относительно какой-либо оси называется произведение массы на квадрат расстояния точки P от этой оси. Квадраты расстояний от точки до осей соответственно равны

тогда моменты инерции находятся по формулам:

Решение физических задач сводится к вычислению тройных интегралов, что было рассмотрено на предыдущем занятии.