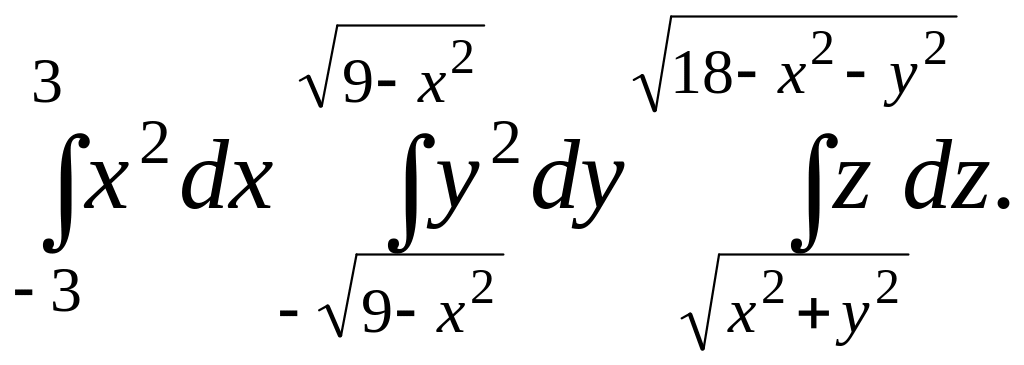Правило вычисления
Построить в плоскости XOY область, на которую проектируется тело объема V, определить линии, ограничивающие эту область.
Записать уравнения поверхностей
и
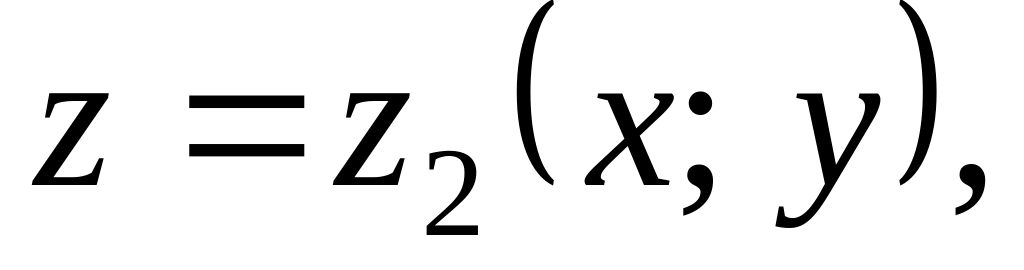ограничивающих объем V
снизу и сверху.Вычислить сначала внутренний интеграл по переменной z, считая x и y постоянными; от полученного результата вычислить средний интеграл по переменной
,
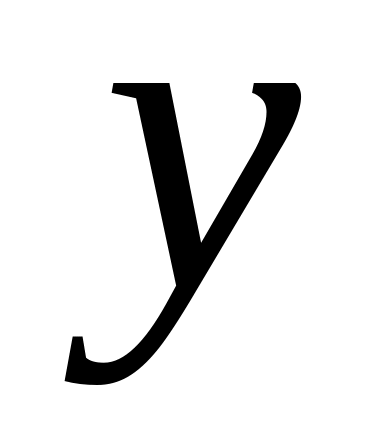считая
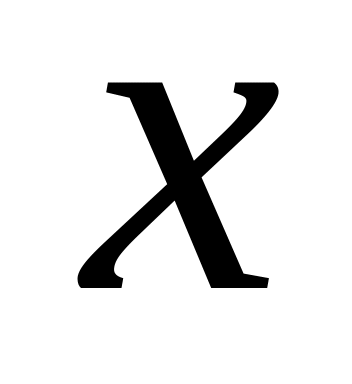постоянной величиной; затем от полученного
результата вычислить внешний интеграл
по переменной х.
Проектировать область V
можно на любую координатную плоскость,
соблюдая свойства правильной трехмерной
области.
1. Вычисление тройных интегралов в декартовых координатах
Задача 1. Вычислить тройной интеграл
где область V ограничена плоскостями:
Решение. Построив данные плоскости, получим треугольную призму (рис. 36). Пользуясь формулой, имеем:
Рис. 36
Ответ: 
Решить самостоятельно по образцу задачи 1. Вычислить трехкратные интегралы и построить их области интегрирования:
Задача
2. 
Задача
3. 
Задача
4. 
Задача
5. 
2. Переход к цилиндрическим координатам в тройном интеграле
Связь декартовых координат и цилиндрических осуществляется по формулам:
где
смысл
виден из рисунка 37.
Рис. 37
Задача 6. Вычислить тройной интеграл
где
область V
ограничена поверхностью
Решение. Построим область V. Методом сечений (аналитическая геометрия в пространстве) имеем:
есть
окружность в плоскости
есть
эллипс в плоскости
YOZ;
есть эллипс в плоскости XOZ.
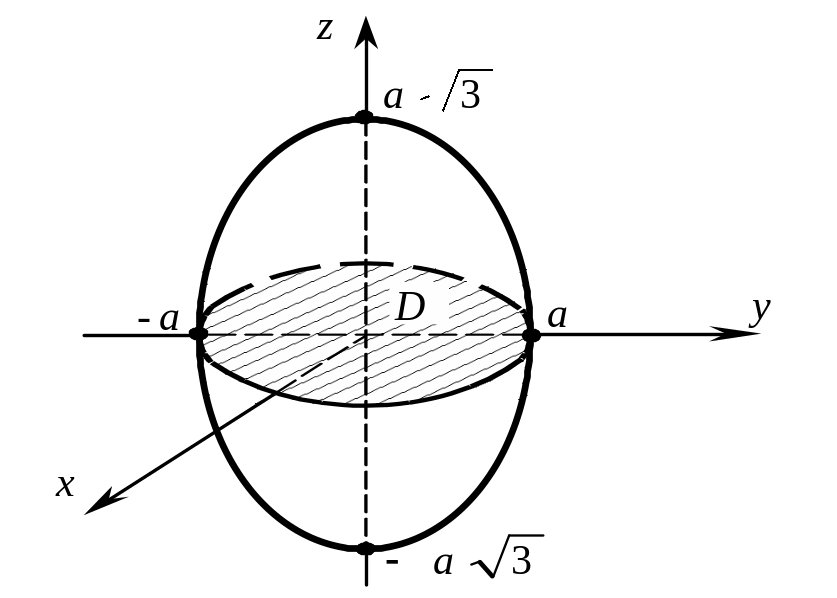
Рис. 38. Эллипсоид вращения
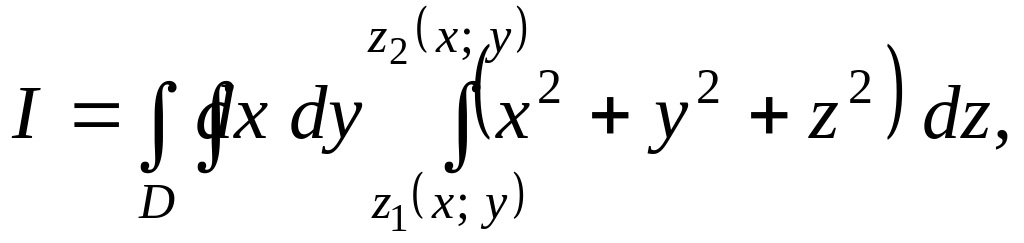
где
находим из уравнения эллипсоида
Вычислим внутренний интеграл по переменной z:
Получим двойной интеграл:
где
область D
в плоскости XOY
есть окружность
В случае «круглой» области D
(как
в нашем случае)
удобно перейти к координатам
Получим
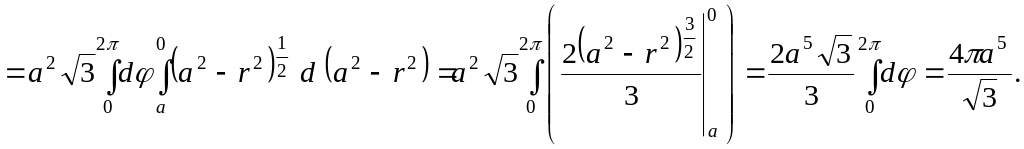
Ответ: 
Задача 7. Решить самостоятельно по образцу задачи 6. Вычислить тройной интеграл
по области V, ограниченной поверхностями
и
Указание. Геометрический
образ
конус,
открытый в сторону
поэтому удобно проектировать конус на
координатную плоскость
XOZ
(рис.
39). Имеем
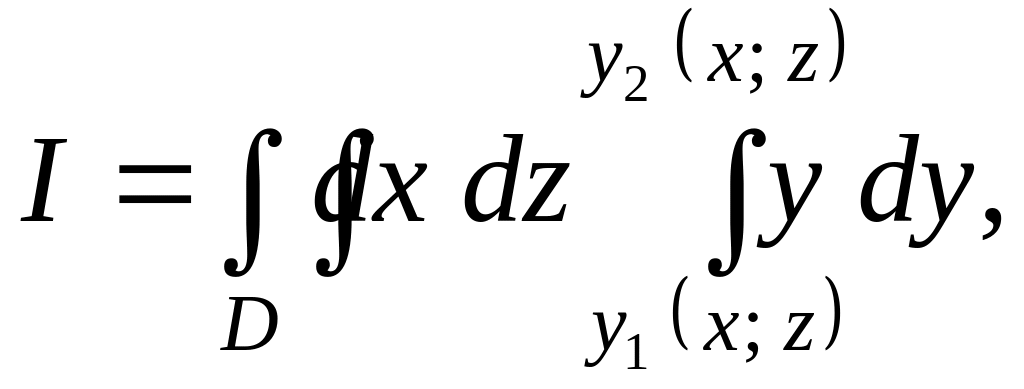
где
При
интегрировании по области D
(окружность) удобно перейти к координатам
уравнение окружности имеет вид:
Рис. 39
3. Переход к сферическим координатам в тройном интеграле
Связь декартовых и сферических координат осуществляется по формулам:
где
смысл
виден из рисунка 40.
Рис. 40
Задача
8. Вычислить
интеграл
где область V
– область, ограниченная поверхностью
Решение. Построим область V, которая представляет собой шар, ограниченный сферой, уравнение которой удобно записать в виде:
(рис.
41).
Рис. 41
Данный интеграл можно вычислить с помощью повторного интегрирования в прямоугольных координатах, но эти вычисления представляют собой определенную сложность.
Удобнее перейти к сферическим координатам:
причем
переменная
изменяется от 0 до
а при каждом значении
переменная Q
изменяется от 0 до
Подставляя сферические координаты в уравнение сферы, получим:
Эти
две поверхности в пространстве
при
ограничивают снизу и сверху область V.
Тогда
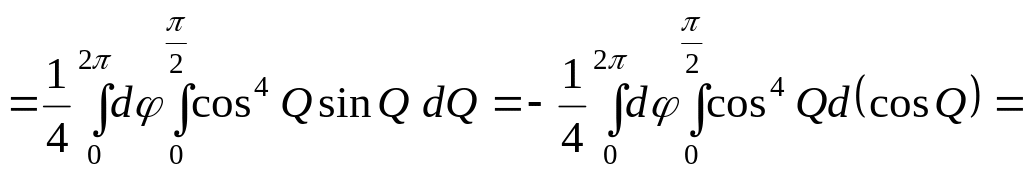
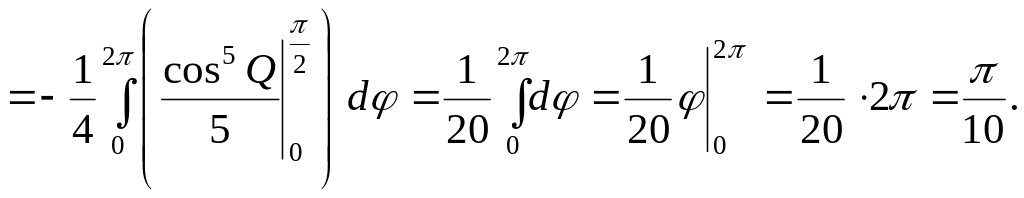
Ответ: 
Задача 9. Решить самостоятельно по образцу задачи 8. Вычислить интегралы, перейдя к сферическим координатам:
а)
где V
– область, ограниченная поверхностью
б)
