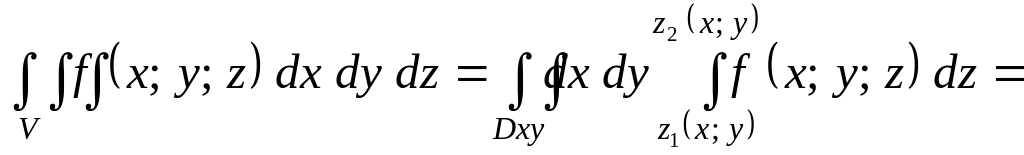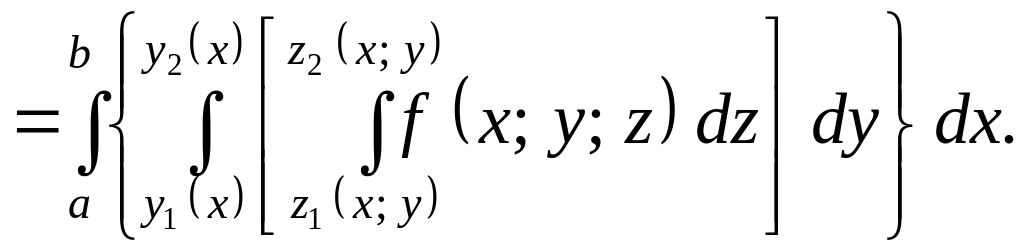1. Криволинейный интеграл по длине дуги (I рода)

Правило вычисления криволинейного интеграла по длине. Для того чтобы криволинейный интеграл

где линия задана параметрическими уравнения и преобразовать в обыкновенный, нужно в подынтегральном выражении положить

и взять интеграл по интервалу изменения t, соответствующему линии интегрирования.

Если уравнение линии имеет вид то дифференциал дуги

Задача 1. Вычислить криволинейный интеграл

где первая арка циклоиды (рис. 33).

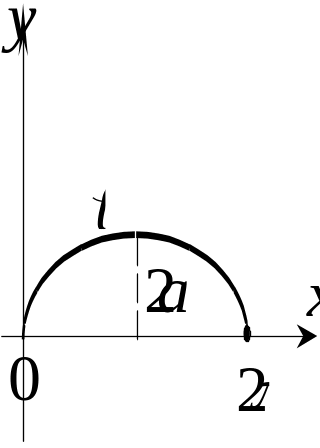
Рис. 33

Решение. Переходим к переменной t, пределы изменения которой для первой арки циклоиды от 0 до

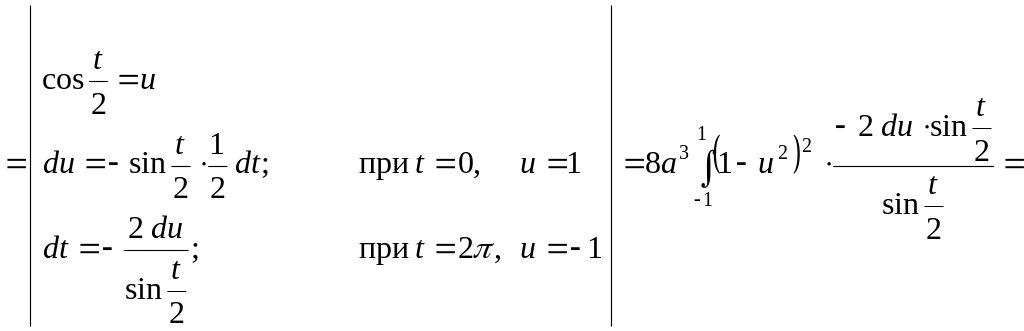
Ответ:

Задача 2. Вычислить криволинейный интеграл:

где отрезок прямой, соединяющий точки и

Решение. Составим уравнение прямой ОА: (рис. 34).

Рис. 34

Следовательно,

Подставим все в интеграл, получим

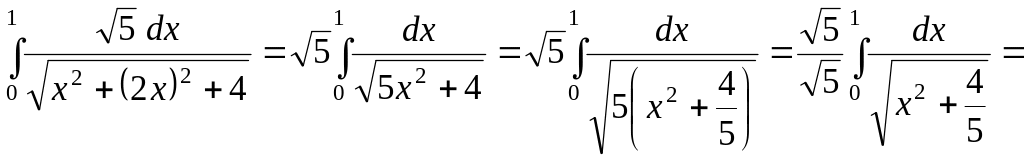
Ответ:

Решить самостоятельно по образцу задач 1 и 2. Вычислить криволинейные интегралы:

Задача 3. где четверть эллипса, лежащая в первом квадранте.

Указание. Параметрические уравнения эллипса

Задача 4. где контур квадрата

2. Криволинейные интегралы второго рода

Правило вычисления криволинейного интеграла по координатам (второго рода).

Для того чтобы криволинейный интеграл

взятый по линии , уравнение которой либо либо преобразовать в обыкновенный интеграл, нужно в подынтегральном выражении заменить либо у через функцию от х в пределах а также выразить либо заменить х, у, dx и dy их выражениями через t и dt в пределах и вычислить получившийся интеграл от одной переменной.

Задача 5. Вычислить интеграл принимая за линию дугу параболы соединяющую точки и (рис. 35).

Решение.

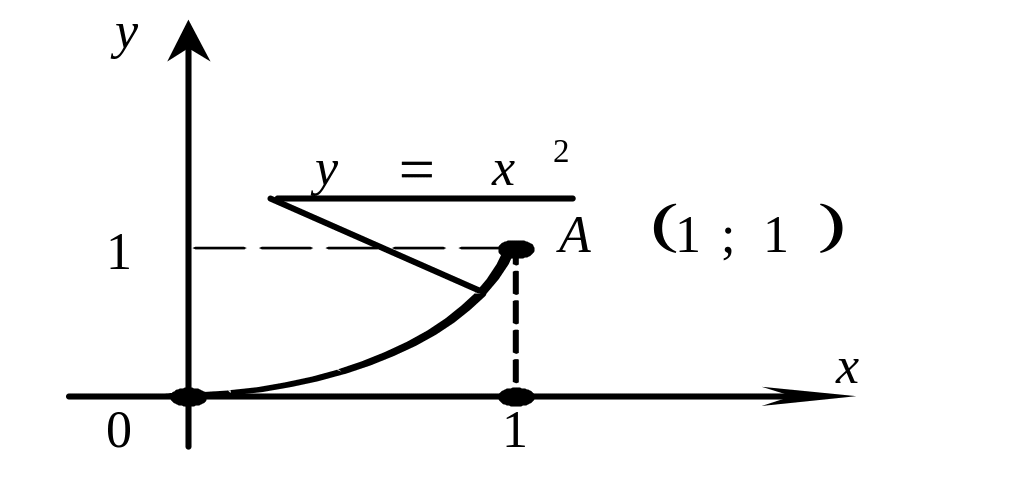
Рис. 35

Т.к.

то

Ответ:

Решить самостоятельно по образцу задачи 5. Вычислить криволинейные интегралы:

Задача 6. где дуга параболы от точки до точки

Задача 7. где дуга первой арки циклоиды пробегаемая в направлении возрастания параметра t.

Задача 8. взятый вдоль отрезка AB биссектрисы второго координатного угла, если абсцисса точки А равна 2 и ордината точки В равна 2.

Задание для самостоятельной работы

Задача 9. Вычислить криволинейный интеграл по дуге параболы заключенной в четвертом квадранте

Задача 10. Вычислить криволинейный интеграл где нижняя часть окружности

Задача 11. Даны точки и Вычислить

1. по прямой OA;

2. по дуге OA параболы

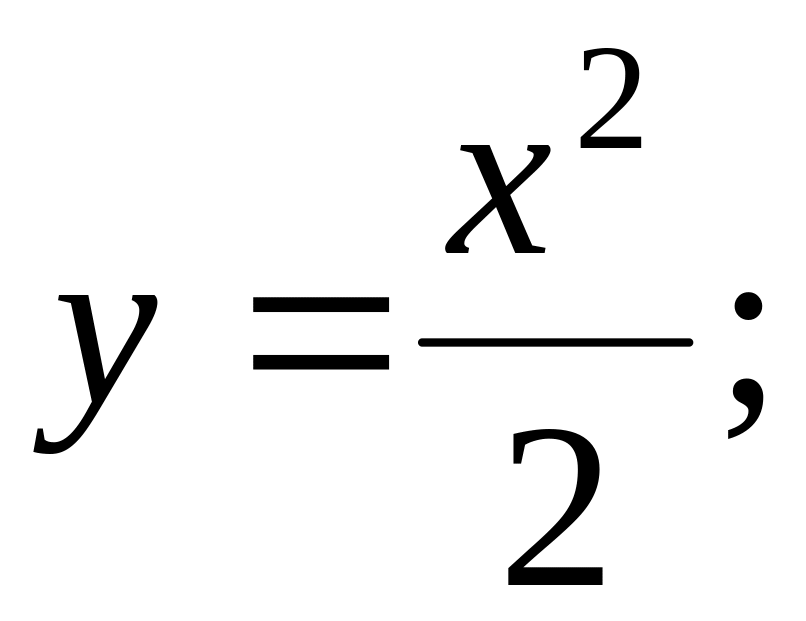
3. по ломаной ОВА.

Задача 12. Вычислить интегралы:

1. 

2. 

3. 

по любой линии от точки до Проверить условие независимости интеграла от пути интегрирования:

не зависит от пути интегрирования от т. М до т. N, если выполняется условие

Занятие №8. Вычисление тройных интегралов

Цель занятия: усвоить правило вычисления тройного интеграла на уровне умения решать типовые задачи.

Учебные вопросы

1. Вычисление тройных интегралов в декартовой системе координат.

2. Переход к цилиндрическим координатам в тройном интеграле.

3. Переход к сферическим координатам в тройном интеграле.

Ход занятия

Теорема. Тройной интеграл от функции по правильной области V равен трехкратному интегралу по той же области, т.е.