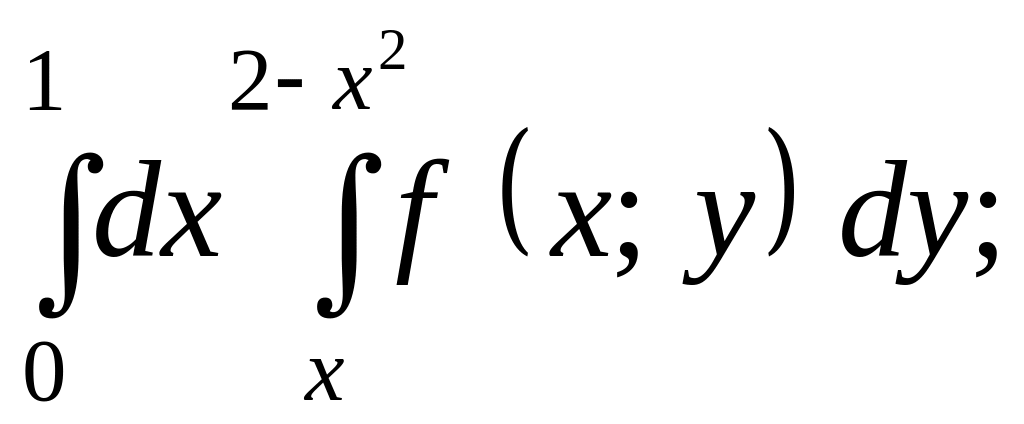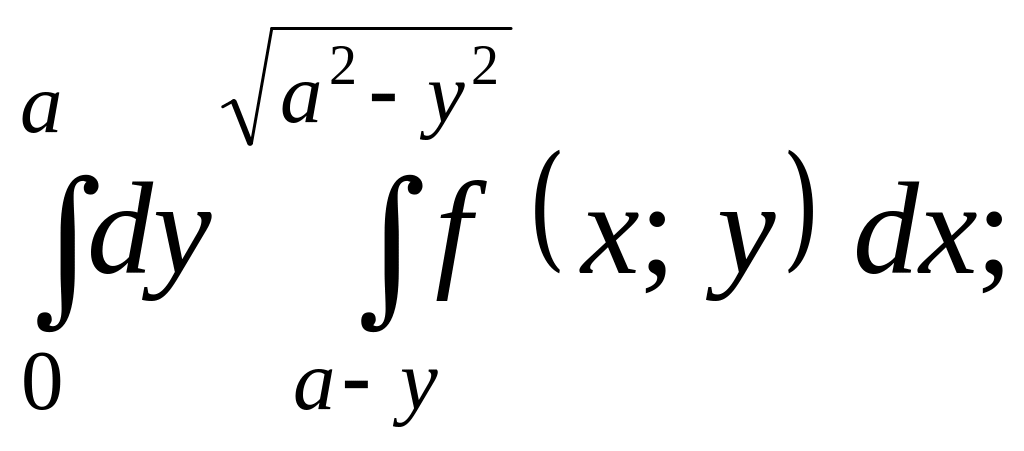Задание для самостоятельной работы

Построить область интегрирования, изменить порядок интегрирования:

6. 

7. 

8. 

9. 

10. 

11. 

12. 

Задача 13. Построить область интегрирования ограниченную линиями, расставить пределы интегрирования в интеграле:

Задача 14. Изменить порядок интегрирования:

Занятие №2. Вычисление двойных интегралов в декартовой системе координат

Цель занятия: усвоить правило вычисления двойного интеграла на уровне умения решать типовые задачи.

Учебные вопросы

1. Вычисление двойных интегралов с данными пределами интегрирования.

2. Расстановка пределов интегрирования и вычисление двойных интегралов.

Ход занятия

Задача 1. Вычислить интегралы:

а) б)

Решение. а) Сначала находим внутренний интеграл:

Полученный результат есть подынтегральная функция для внешнего интеграла:

б) Вычисление начинаем с внутреннего интеграла, где у является переменной, а х – постоянной (при интегрировании постоянная величина выносится за знак интеграла).

Далее вычисляем внешний интеграл, полученный результат интегрируем по х:

Ответ: а) 4; б)

Задача 2. Решить самостоятельно по образцу задачи 1. Вычислить двукратные интегралы:

1)

2)

3)

4)

5) .

Задача 3. Вычислить двойной интеграл

если

Решение. 1. Построим область интегрирования D (рис. 11).

Рис. 11

2. Определим порядок интегрирования по виду области D. Удобно в повторном интеграле внутреннее интегрирование выполнять по у, а внешнее по х. Тогда:

3. Найдем пределы интегрирования внешнего интеграла: Значение найдем, решая совместно уравнения:

Переменная у изменяется в области от ее значения на нижней части контура до ее значения на верхней части контура. Таким образом:

Вычислим внутренний интеграл:

Затем вычислим внешний интеграл:

Ответ:

Задача 4. Решить самостоятельно по образцу задачи 3. Перейти к двукратному интегралу и вычислить его по данной области:

1. 

2. 

3. 

4. 

5. 

6. 

Задача 5. Вычислить двукратные интегралы:

1. 

2. 

3. 

Задача 6. Вычислить двойной интеграл

по области D, ограниченной треугольником с вершинами

Занятие №3. Вычисление двойных интегралов в полярной системе координат

Цель занятия: усвоить правило вычисления двойного интеграла в полярных координатах на уровне умения решать типовые задачи.

Учебные вопросы

1. Вычисление двойных интегралов в полярной системе координат.

2. Переход от декартовых координат к полярным при вычислении двойных интегралов.

Ход занятия

Вспомним, что если область интегрирования двойного интеграла отнесена к системе полярных координат то и обычно

(*)

Задача 1. Решить самостоятельно. Вычислить интеграл:

Задача 2. Вычислить интеграл:

где окружность радиуса а.

Решение. Построим окружность Видим, что r изменяется от 0 до а, а - от 0 до (рис. 12).

Воспользуемся формулой (*), получим:

Вычисление начинаем, как обычно, с внутреннего интеграла:

Затем

Ответ:

Рис. 12	Рис. 13

Задача 3. Вычислить двойной интеграл

где область ограничена линиями и

Решение. Построим область D (рис. 13).

Чтобы определить, как изменяется в области полярный угол проведем лучи в точки А и В области D. Решая совместно уравнения линий, ограничивающих область D, найдем значения угла

Теперь найдем пределы изменения полярного радиуса r. Из полюса проведем произвольный радиус. Видим, что он пересекает линию а при выходе из области – линию

По формуле (*):

Внутренний интеграл:

Внешний интеграл:

Ответ:

Задача 4. Решить самостоятельно по образцу задач 2 и 3. Вычислить двойной интеграл

если область D:

1. круговой сектор, ограниченный линиями

2. полукруг

3. заключена между линиями

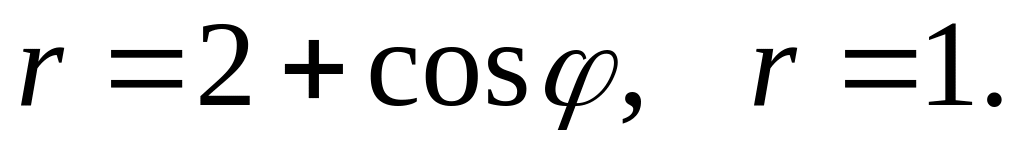
Задача 5. Преобразовать к полярным координатам и затем вычислить двойной интеграл

где круговое кольцо, заключенное между окружностями и

Решение. Пользуясь формулами связи декартовых и полярных координат