Тема 6. Интегральное исчисление функции двух переменных

Учебно-воспитательные цели: усвоить правила вычисления кратных и криволинейных интегралов на уровне знания и умения решать типовые задачи по теме; уметь применять двойные и криволинейные интегралы к решению прикладных задач.

Краткая информация о новых учебных элементах

Двойной интеграл

1. Двойной интеграл в декартовых координатах

Двойным интегралом от функции по области D плоскости называется предел интегральной суммы при условии, что наибольший из диаметров частичных областей стремится к нулю.

Основные свойства двойного интеграла

1. 

2. где

Если область интегрирования D разбита на две области и то

Правила вычисления двойных интегралов

Различают два основных вида области интегрирования.

1. Область интегрирования D ограничена слева и справа прямыми и а снизу и сверху – непрерывными кривыми и каждая из которых пересекается вертикальной прямой только в одной точке (рис. 1).

Рис. 1	Рис. 2

Для такой области двойной интеграл вычисляется по формуле:

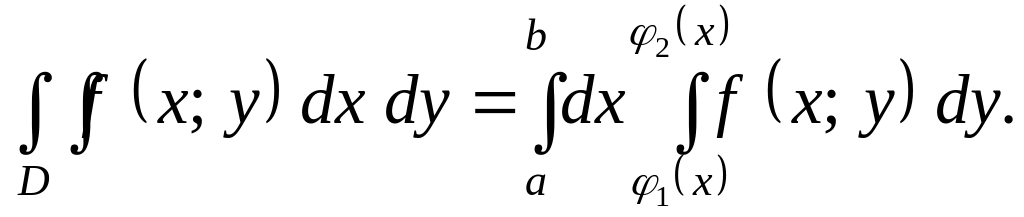
Причем сначала вычисляется внутренний интеграл в котором х считается постоянной величиной.

2. Область интегрирования D ограничена снизу и сверху прямыми и а слева и справа – непрерывными кривыми: и каждая из которых пересекается горизонтальной прямой только в одной точке (рис. 2).

Для такой области двойной интеграл вычисляется по формуле:

Причем сначала вычисляется внутренний интеграл в котором у считается постоянной величиной. В более общем случае область интегрирования путем разбиения на части сводится к основным.

2. Двойной интеграл в полярных координатах

Переход двойного интеграла от прямоугольных координат к полярным координатам связанным с прямоугольными координатами соотношениями осуществляется по формуле

Если область интегрирования D ограничена двумя лучами и выходящими из полюса, и двумя кривыми и где и однозначные функции при и то двойной интеграл вычисляется по формуле:

где причем сначала вычисляется интеграл в котором считается постоянной величиной.

3. Решение геометрических задач с помощью двойного интеграла

1. Вычисление площади плоской фигуры.

Площадь плоской фигуры, ограниченной областью D, находится по формулам:

в декартовых координатах:

в полярных координатах:

2. Вычисление объема тела.

Объем цилиндрического тела, ограниченного сверху непрерывной поверхностью снизу плоскостью и сбоку прямой цилиндрической поверхностью, вырезающей на плоскости область D, вычисляется по формуле:

4. Решение физических задач с помощью двойного интеграла

1. Вычисление массы плоской пластинки.

Если пластинка занимает область D плоскости и имеет переменную поверхностную плотность то масса пластинки выражается двойным интегралом:

2. Вычисление моментов инерции пластинки.

Момент инерции пластинки относительно оси

Момент инерции пластинки относительно оси

Момент инерции относительно начала координат:

3. Вычисление статистических моментов пластинки относительно осей Ох и Оу соответственно:

4. Вычисление координат центра тяжести (центра масс) однородной плоской пластинки: