§ 1. Теплопередача через плоскую стенку
Пусть однослойная плоская стенка (рис. 37) толщиной из материала, коэффициент теплопроводности которого , омывается с одной стороны горячей жидкостью с температурой tж1, с другой стороны холодной жидкостью с температурой tж2. Значения коэффициентов теплоотдачи от горячей жидкости к стенке и от стенки к холодной жидкости соответственно 1 и 2.
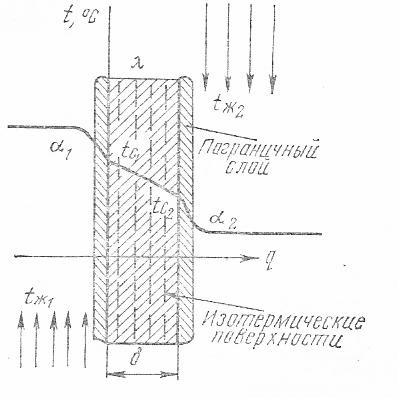
Рис. 37. Схема теплопередачи через плоскую стенку.
Средние значения температур поверхностей стенки tс1 и tс2. Количество теплоты, передаваемой от горячей жидкости (газа) к стенке, равно количеству теплоты, передаваемой от стенки к нагреваемой жидкости (газу).
Если считать тепловой поток отнесенным к 1 м2 площади стенки, то можно записать систему уравнений:
q = 1 (tж1 – tс1);
q = / (tс1 – tс2); (162)
q = 2 (tс2 – tж2).
Каждое из этих уравнений представим в виде:
q
(1/1)
= tж1 – tс1;
+ q (/) = tс1 – tс2; (163)
q (1/2) = tс2 – tж2.
Сложив, получим расчетную формулу для плотности теплового потока:
(164)
Последнее выражение можно переписать так:
q = K (tж1 – tж2), (165)
где К =
– коэффициент теплопередачи. (166)
Коэффициент теплопередачи К численно равен плотности теплового потока q при разности температур теплоносителей в 1 К.
Величина, обратная коэффициенту теплопередачи, называется термическим сопротивлением теплопередачи и равна сумме термических сопротивлений теплоотдачи 1/1, 1/2 и термического сопротивления теплопроводности /:
R = 1/K = 1/1 + 1/2 + /. (167)
Если плоская стенка состоит из нескольких слоев, каждый из которых однороден и плотно прилегает к другому (то есть отсутствует термическое сопротивление контакта), то общее термическое сопротивление многослойной стенки будет равно:
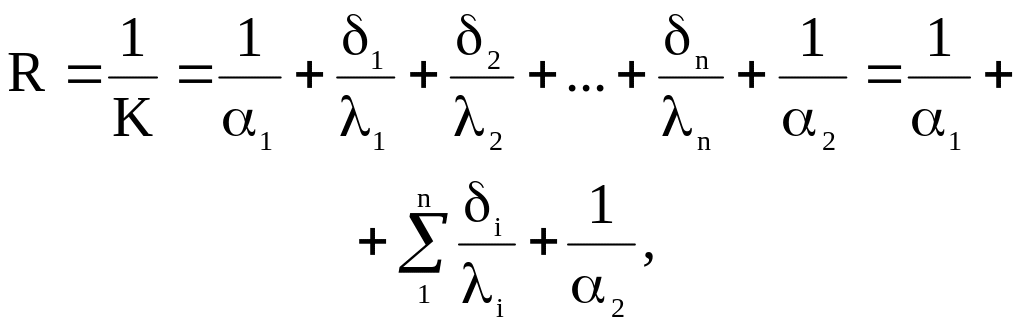(168)
где i, i – соответственно толщина каждого из слоев многослойной стенки и коэффициенты теплопроводности материала каждого слоя.
Удельный тепловой поток для этого случая подсчитывается по формуле:
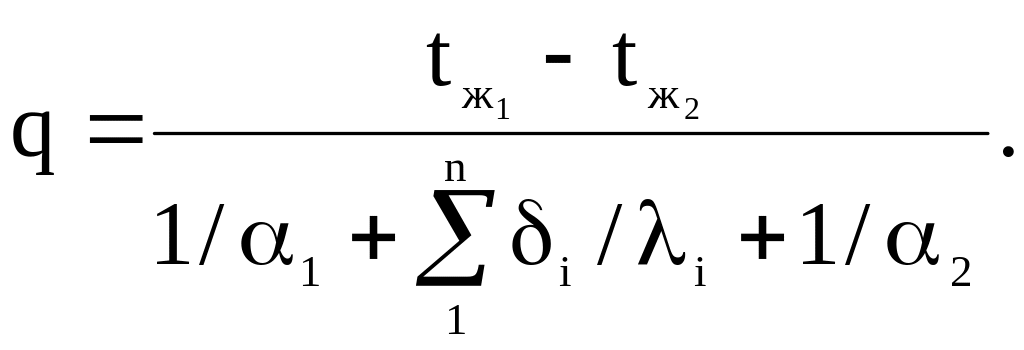(169)
§ 2. Теплопередача через цилиндрическую стенку
В практике наиболее распространенным элементом теплообменных устройств является труба. Схема процесса теплопередачи через цилиндрическую стенку (трубу) представлена на рисунке 38.
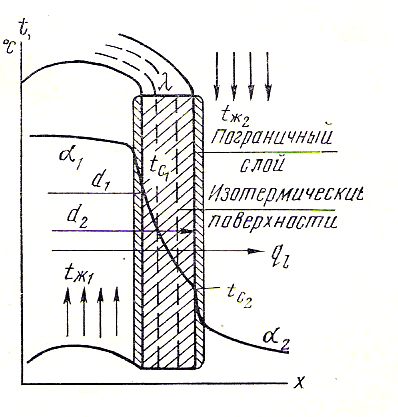
Рис. 38 Схема теплопередачи через цилиндрическую стенку.
Пусть цилиндрическая стенка изнутри омывается горячим теплоносителем с температурой tж1, коэффициент теплоотдачи от горячей жидкости к внутренней стенке 1. С наружной стороны труба омывается холодным (нагреваемым) теплоносителем с температурой tж2, коэффициент теплоотдачи от наружной стенки к холодному теплоносителю 2. Коэффициент теплопроводности материала стенки , внутренний диаметр трубы d1, наружный – d2. Если длина трубы ℓ (м), то можно записать для мощности теплового потока Q (Вт) следующие выражения:
Q = 1 F1 (tж1 – tс1) = 1 d1 (tж1 – tс1);
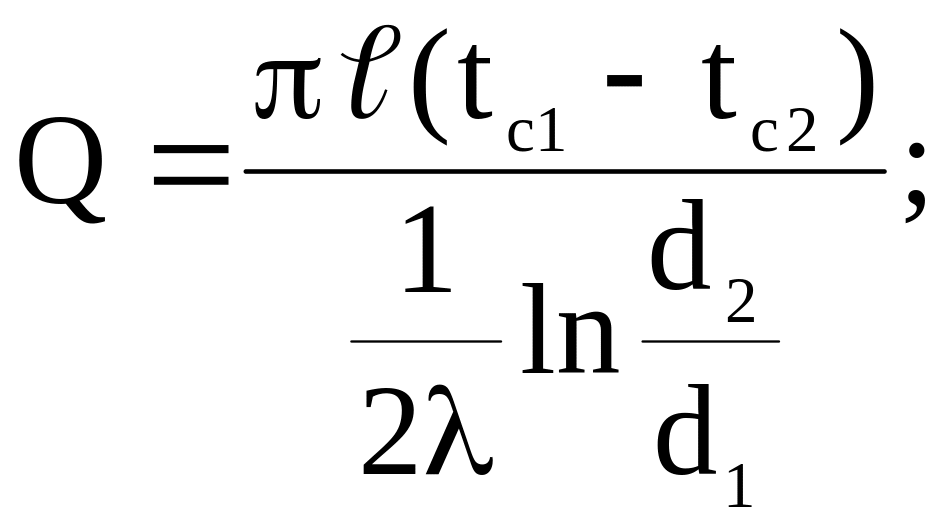
Q = 2 F2 (tc2 – tж2) = 1 d2 ℓ (tс2 – tж2). (170)
Решив данную систему уравнений и представив Q/ℓ = q1 (удельный тепловой поток на 1 м длины трубы), получим:
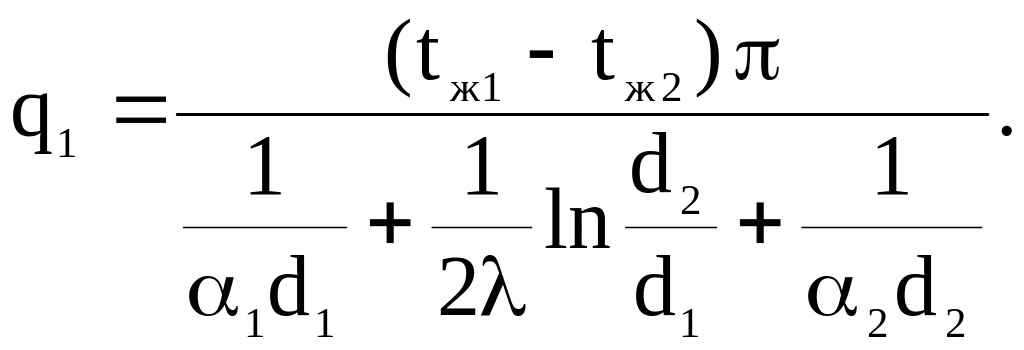(171)
В последнем выражении величина:
(172)
называется линейным коэффициентом теплопередачи, который показывает количество теплоты, проходящей через цилиндрическую стенку длиной 1 м в течение 1 с при разности температур теплоносителей 1 К. Величина:
(173)
называется линейным термическим сопротивлением теплопередачи.
Для многослойной цилиндрической стенки линейный коэффициент теплопередачи Kℓ можно рассчитать по формуле:
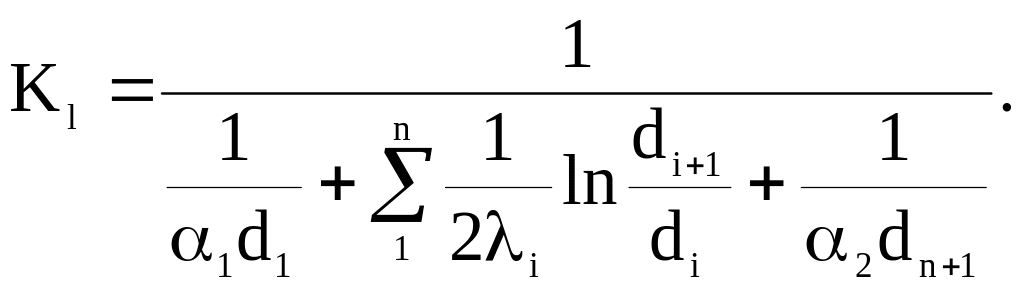(174)
Вывод этого выражения может быть выполнен самими учащимися.