§ 2. Закон фурье

Закон Фурье устанавливает количественную взаимосвязь между температурным полем и интенсивностью распространения теплоты в нем посредством теплопроводности. Согласно закону Фурье, вектор плотности теплового потока ( ) пропорционален вектору градиента температуры (grad t) и противоположен по направлению:

= –  grad t, (141)

где знак «–» показывает, что векторы градиента температуры и плотности теплового потока направлены в противоположные стороны; коэффициент пропорциональности  – коэффициент теплопроводности – численно равен плотности теплового потока при градиенте температуры 1 к/м.

Размерность коэффициента теплопроводности – Вт/(м ^. К). Коэффициенты теплопроводности различных веществ зависят от структуры, влажности, давления и температуры и приводятся в виде таблиц и графиков в справочной литературе.

Например, при возрастании плотности асбеста от 400 до 800 кг/м³ его коэффициент теплопроводности возрастает от 0,105 до 0,248 Вт/(м ^. К). Если теплопроводность сухого кирпича равна 0,35 Вт/(м ^. К), то влажного – 1,0 Вт/(м ^. К). Коэффициент теплопроводности воды при 20 ⁰С и давлении 0,1 МПа равен 0,6 Вт/(м ^. К), воздуха (при тех же условиях) – 0,026 Вт/(м ^. К). Коэффициенты теплопроводности чистых металлов могут достигать больших значений: меди – 396 Вт/(м ^. К), алюминия – 250 Вт/(м ^. К).

Материалы, коэффициент теплопроводности которых менее 0,25 Вт/(м ^. К), называются теплоизоляционными.

Для решения практических задач по определению интенсивности переноса теплоты теплопроводностью применяются расчетные формулы, полученные на основе закона Фурье. Эти формулы наиболее просты при стационарном тепловом режиме, то есть когда температуры в любой точке тела в течение времени не изменяются, а температурное поле однородно.

§ 3. Частные случаи теплопроводности

ПРИ СТАЦИОНАРНОМ РЕЖИМЕ

Теплопроводность однослойной плоской стенки. Схема распространения теплоты для этого случая приведена на рисунке 30. Пусть теплота распространяется в стенке, ограниченной параллельными плоскостями площадью F (м²).

Рис. 30. Схема передачи теплоты теплопроводностью через плоскую однородную стенку.

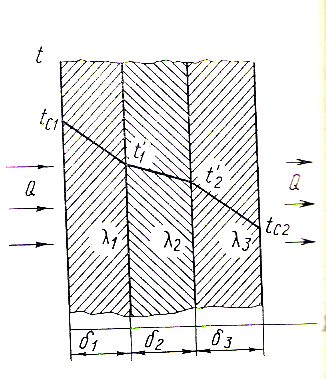
Рис. 31. Схема передачи теплоты теплопроводностью через плоскую многослойную стенку.

Будем считать, что температуры на поверхностях стенки t_с1 и t_с2 не изменяются во времени. Так как стенка однородна, то изотермические поверхности внутри стенки располагаются параллельно ее боковым граням. Согласно закону Фурье, тепловой поток Q (Вт), проходящий через стенку, прямо пропорционален поверхности F, разности температур t_с1– t_с2 и обратно пропорционален толщине стенки  (м):

Q =  F . (142)

Плотность теплового потока q (Вт/м²) определяют из выражения:

q = Q/F = . (143)

Величину /, м^{2 .} К/Вт, называют термическим сопротивлением теплопроводности.

Если последнее уравнение переписать относительно t_с2, то можно установить, что температура внутри плоской стенки изменяется по закону прямой линии.

Теплопроводность многослойной плоской стенки. На практике, как правило, рассчитывают передачу теплоты теплопроводностью через многослойные стенки. Например, обмуровка парового котла состоит из слоя огнеупорного кирпича, соприкасающегося с наиболее нагретыми элементами топки, и наружного слоя красного кирпича. Часто стенки имеют слой штукатурки и поверхностной окраски.

Рассмотрим определение теплового потока теплопроводностью через многослойную стенку. Расчетная схема представлена на рисунке 31. Пусть стенка состоит из трех слоев, толщина каждого из которых соответственно ₁, ₂, ₃, а коэффициенты теплопроводности ₁, ₂, ₃, Температуры наружных поверхностей t_с1 и t_с2, температуры внутри стенки на границе слоев t₁ и t₂. Записав формулу (143) для каждого из трех слоев, после преобразований получим:

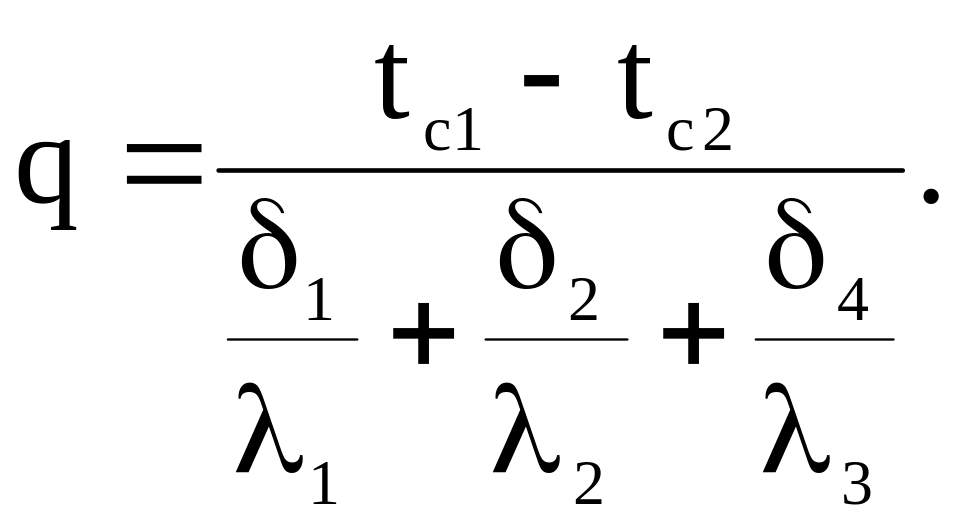(144)

Для многослойной плоской стенки, имеющей n слоев, запишем:

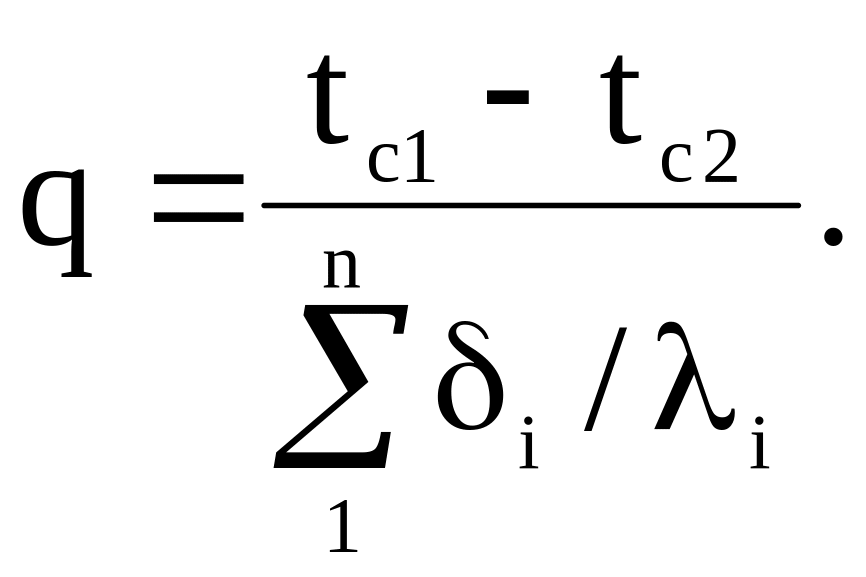(145)

Теплопроводность одно- и многослойной цилиндрических стенок. В практике часто имеют место случаи передачи теплоты теплопроводностью через однослойную и многослойную цилиндрические стенки (например, через стенку паропровода). Расчетная схема для этого случая представлена на рисунке 32.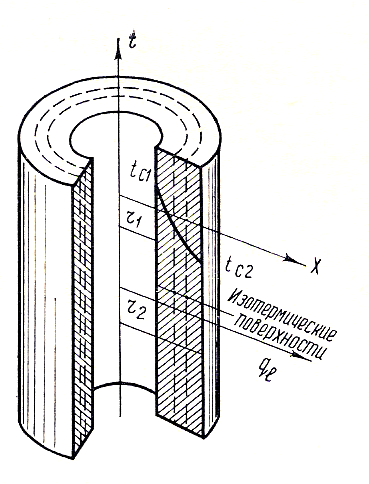

Рис. 32. Схема передачи теплоты теплопроводностью через однослойную однородную цилиндрическую стенку.

Внешняя и внутренняя поверхности цилиндрической стенки длиной 1 м имеют постоянные во времени температуры t_с1 и t_с2. Внутренний диаметр d₁, наружный – d₂. Материал трубы имеет коэффициент теплопроводности . Величину линейной (в расчете на 1 м длины) плотности теплового потока q₁ определяют по формуле:

(146)

Из данного выражения видно, что температура внутри цилиндрической стенки изменяется по логарифмическому закону.

Для многослойной цилиндрической стенки, имеющей n слоев, согласно уравнению (146) можно записать:

(147)

Контрольные вопросы и задания. 1. Дайте определение теплообмена и теплопроводности. 2. Что такое температурное поле? Какие бывают температурные поля? 3. Расскажите о градиенте температуры и о плотности теплового потока. 5. Напишите выражения для подсчета плотности теплового потока через плоскую и цилиндрическую стенки.