Матрица Основные определения

Определение 1. Матрицей¹⁾   размера   с элементами из множества   называется семейство   элементов из  , пронумерованных упорядоченными парами натуральных чисел  , где  ,  . При этом пишут

или, более кратко,  . Для фиксированного   семейство   называется  -й строкой²⁾ матрицы  . При фиксированном   семейство   называется  -м столбцом³⁾ матрицы  . Матрица размера   называетсястрокой⁴⁾, матрица размера   — столбцом⁵⁾.

Определение 2. Матрица   размера   называется квадратной матрицей⁶⁾ порядка  .

Определение 3. Пусть   — матрица порядка  . Множество   называется главной диагональю⁷⁾ матрицы.

Как правило, от множества   требуется, чтобы оно было полем или кольцом.

Определение 4. Пусть   — матрица порядка  . Следом матрицы⁸⁾   называется сумма элементов на ее главной диагонали:  .

Определение 5. Пусть   — матрица порядка   с элементами из кольца  . Матрица   называется диагональной⁹⁾ и обозначается как  , если   при  .

Определение 6. Пусть   — матрица порядка   с элементами из кольца  . Матрица   называется верхней треугольной¹⁰⁾, если   при  .

Определение 7. Пусть   — матрица порядка   с элементами из кольца  . Матрица   называется нижней треугольной¹¹⁾, если   при  .

Определение 8. Пусть   — диагональная матрица порядка   с элементами из кольца  . Матрица   называется скалярной¹²⁾, если все ее элементы на главной диагонали одинаковы.

Определение 9. Скалярная матрица   порядка   с элементами из кольца   называется единичной¹³⁾, если все ее элементы на главной диагонали равны 1.

Определение 10. Матрица   называется симметричной¹⁴⁾, если   для всех  .

Определение 11. Матрица   называется кососимметричной¹⁵⁾, если   для всех  .

Пример 1. Матрица вида   является верхнетреугольной матрицей порядка 2.

Операции над матрицами Транспонирование

Пусть   — матрица порядка  .

Определение 12. Матрица   порядка   называется матрицей, транспонированной¹⁶⁾ к  .

Сложение и умножение на скаляр

Пусть   и   — матрицы размера   над кольцом  .

Определение 13. Матрица   размера   с элементами   называется суммой матриц   и  .

Определение 14. Умножение матрицы   на скаляр   определяется правилом:  .

Предложение 1. Относительно введенных операций сложения и умножения на скаляр множество всех матриц размера  над полем   образует векторное пространство размерности  .

Векторное пространство матриц порядка   над полем   обозначается  .

Умножение матриц

Пусть   и   — матрицы над кольцом   размера   и   соответственно.

Определение 15. Произведение матриц   и   определено, если  . Результатом умножения является матрица   размера   с элементами  .

Пример 2. Произведением матрицы   размера   и столбца   является столбец  .

Предложение 2. Умножение матриц ассоциативно, то есть  , если определены   и  .

Пример 3. Умножение матриц не коммутативно:  , что не равно  .

Предложение 3. Если умножение соответствующих матриц определено, то

• ;

• .

Предложение 4. Относительно матричного умножения пространство   матриц над полем   является ассоциативнойалгеброй над  .

Матрица линейного отображения Определение

Определение 1. Пусть   и   — конечномерные векторные пространства над полем   сбазисами   и   соответственно. Рассмотрим линейное отображение  . Тогда   можно представить в виде   для некоторых  . Матрица   называется матрицей линейного отображения¹⁾   в базисах   и  . Столбцами этой матрицы являются координаты векторов   в базисе  .

Пусть произвольный вектор   имеет следующие координаты в разложении по базису  ,  , тогда его образ   из пространства   в базисе   имеет разложение  , где  . То есть .

Предложение 1. Существует взаимно однозначное отображение между множеством всех линейных отображений из  -мерного векторного пространства   в  -мерное векторное пространство   с фиксированными базисами и множеством матриц размера  .

Определение 2. Матрица линейного оператора²⁾ — это матрица линейного отображения в случае, когда  .

Пример 1. Пусть   — базис  -мерного векторного пространства  . Рассмотрим тождественный³⁾ линейный оператор . Так как  , то матрица   — это в точности единичная матрица .

Предложение 2. Пусть   — конечномерные векторные пространства,   и   — линейные отображения. Тогда  .

Умножением двух линейных операторов   и   на пространстве   будем считать их композицию:  . Тогда справедливо

Предложение 3. Пространство линейных операторов   является ассоциативной алгеброй над полем  . В случае, если пространство   конечномерно, алгебра   изоморфна алгебре всех матриц порядка   над полем  . Изоморфизм задается отображением  .

Минимальный многочлен линейного оператора

Пусть   — конечномерное векторное пространство над полем   и   — линейный оператор на  .

Определение

Определение 1. Многочлен   минимальной степени, аннулирующий оператор  , то есть  , называетсяминимальным многочленом¹⁾ линейного оператора  .

Определитель и след линейного оператора

Определение

Пусть   — линейный оператор с матрицей   в некотором фиксированном базисе   векторного пространства   над полем  .

Определение 1. Определителем¹⁾   линейного оператора   называется определитель матрицы  .

Определение 2. Следом²⁾   линейного оператора   называется след матрицы  .

Предложение 1. Пусть   — характеристический многочлен оператора  . Тогда

1. ,

2. .

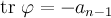Следствие 1. Определитель и след линейного оператора   не зависят от выбора базиса пространства  .

Пример 1. Определитель и след нулевого линейного оператора равны нулю.

Пример 2. Определитель тождественного линейного оператора на  -мерном векторном пространстве   равен  , а его след равен  .

Предложение 2. Отображение  , которое каждому эндоморфизму   ставит в соответствие его след  , линейно.