Положительная определенность

Определение 3. Квадратичная форма называется невырожденной, если ее ранг равен размерности  .

Определение 4. Квадратичная форма называется

1. положительно определенной, если   для всех ненулевых  ;

2. отрицательно определенной, если   для всех ненулевых  ;

3. положительно полуопределенной, если   для всех  ;

4. отрицательно полуопределенной, если 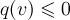  для всех  ;

5. неопределенной, если она принимает как положительные, так и отрицательные значения.

Пример 1. Пусть   имеет в некотором базисе   нормальный вид  , тогда  положительно определена.

Линейная зависимость

Пусть   — (левый) модуль над ассоциативным кольцом  . Частным случаем такого модуля является векторное пространство   над полем  .

Линейные комбинации. Линейная оболочка

Пусть   — некоторое подмножество элементов из  .

Определение 1. Линейной комбинацией¹⁾ элементов из   называют сумму  , где лишь конечное число элементов   отлично от нуля. Элементы   называются коэффициентами²⁾ линейной комбинации.

Пример 1. Кольцо многочленов   над полем   является, в частности, векторным пространством. Пусть  . Линейная комбинация этих векторов   — это многочлен степени 2.

Предложение 1. Множество всех линейных комбинаций элементов из   является подмодулем в модуле  .

Определение 2. Пусть   — множество всех линейных комбинаций элементов из  , тогда   называется подмодулем,порожденным  , или  -линейной оболочкой³⁾ множества  , и обозначается  . При этом   называют множествомобразующих⁴⁾ для  .

В частном случае векторного пространства   над полем   данное определение можно переформулировать следующим образом:

Определение 2'. Линейной оболочкой⁵⁾ подмножества   линейного пространства   называется множество   всех линейных комбинаций векторов из  . Говорят также, что оболочка   порождена векторами  , или что оболочка   натянута на вектора  .

Пример 2. В кольце многочленов   над полем   выберем множество  . Линейную оболочку  составляют всевозможные многочлены  , то есть  .

Пример 3. Кольцо многочленов от двух переменных   можно рассматривать как левый модуль над кольцом  . Пусть , тогда  -линейная оболочка множества   состоит из элементов  , где  . Таким образом,  .

Линейная зависимость

Определение 3. Набор элементов   модуля   называется линейно независимым⁶⁾ над  , если из равенства нулю линейной комбинации   следует, что   для всех  . Если же существует соотношение  , в котором не все   равны нулю, элементы из   называют линейно зависимыми⁷⁾.

Если в качестве модуля взять векторное пространство   и рассматривать конечные наборы  , то определение линейной зависимости может быть переформулировано следующим образом:

Определение 3'. Система векторов   пространства   называется линейно зависимой⁸⁾, если найдутся числа  , не равные нулю одновременно и такие, что  . В противном случае векторы   называются линейно независимыми.

Пример 4. Если множество   содержит нулевой элемент, то оно линейно зависимо.

Предложение 2. Пусть   — векторное пространство над полем  . Имеют место следующие утверждения:

1. система векторов   с линейно зависимой подсистемой линейно зависима,

2. любая часть линейно независимой системы векторов   линейно независима,

3. среди линейно зависимых векторов   хотя бы один является линейной комбинацией остальных,

4. если один из векторов   выражается через остальные, то векторы   линейно зависимы,

5. если векторы   линейно независимы, а   — линейно зависимы, то   — линейная комбинация векторов  ,

6. если векторы   линейно независимы и вектор   нельзя через них выразить, то система  линейно независима.