
- •Список основных статей по линейной алгебре
- •Аффинное пространство Точечно-векторная аксиоматика аффинного пространства
- •Для всех .
- •Базис и размерность векторного пространства Определение
- •Переход от одного базиса к другому
- •Билинейное отображение Определение
- •Билинейная форма
- •Матрица билинейной формы
- •Векторное пространство Определение
- •Подпространство векторного пространства
- •Для любых векторов ;
- •Для всех .
- •Факторпространство
- •Двойственное векторное пространство Определение
- •Для всех ;
- •Для всех .
- •Корневые подпространства
- •Квадратичная форма Определение
- •Квадратичная форма на векторном пространстве Определение
- •Матрица квадратичной формы
- •Квадратичная форма на вещественном векторном пространстве
- •Закон инерции квадратичных форм
- •Положительная определенность
- •Линейная зависимость
- •Линейные комбинации. Линейная оболочка
- •Линейная зависимость
- •Линейное нормированное пространство Определение
- •Линейное отображение векторных пространств Определение
- •Для всех ;
- •Для всех , .
- •Частные случаи
- •Свойства линейного отображения
- •Матрица Основные определения
- •Операции над матрицами Транспонирование
- •Сложение и умножение на скаляр
- •Умножение матриц
- •Матрица линейного отображения Определение
- •Определитель матрицы Определитель
- •Свойства определителя
- •Пересечение и сумма подпространств Пересечение и сумма
- •Внутренняя прямая сумма
- •Внешняя прямая сумма
- •Ранг матрицы Горизонтальный и вертикальный ранг
- •Элементарные преобразования матрицы
- •Минорный ранг
- •Свободный модуль Определение
- •Скалярное произведение Скалярное произведение
- •Евклидово пространство
- •Теорема Лапласа Минор
- •Алгебраическое дополнение
- •Теорема Лапласа
- •Определители 2-го порядка
- •Определители 3-го порядка
- •Определители высших порядков
- •Характеристический многочлен линейного оператора
- •Инвариантные подпространства
- •Собственные вектора и собственные значения
- •Характеристический многочлен
- •Диагонализируемые линейные операторы
- •Системы линейных уравнений Правило Крамера
- •7. 1 Линейные операторы и действия над ними
- •Базис и размерность пространства
Системы линейных уравнений Правило Крамера
Задача 1. Решить систему линейных уравнений

Решение. Согласно
правилу Крамера, если определитель
системы ![]() ненулевой,
то система имеет единственное решение,
определенное формулами:
ненулевой,
то система имеет единственное решение,
определенное формулами:
![]() .
.
Найдем , раскладывая определитель по двум первым строкам (см. теорему Лапласа):
 .
.Найдем определитель
 ,
который получается из
заменой
первого столбца на столбец свободных
членов:
,
который получается из
заменой
первого столбца на столбец свободных
членов:




 .
.Найдем определитель
 ,
который получается из
заменой
второго столбца на столбец свободных
членов:
,
который получается из
заменой
второго столбца на столбец свободных
членов:




 .
.Найдем определитель
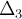 ,
который получается из
заменой
третьего столбца на столбец свободных
членов:
,
который получается из
заменой
третьего столбца на столбец свободных
членов:




 .
.Найдем
 ,
который получается из
заменой
последнего столбца на столбец свободных
членов:
,
который получается из
заменой
последнего столбца на столбец свободных
членов:

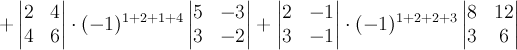


 .
.
Таким
образом, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
5.1.5. Образ и ядро линейного оператора
Рассмотрим линейный оператор A, действующий в пространстве Rn.
Напомним, что множество элементов пространства Rn, которые являются образами элементов из области определения D(A) оператора A, называют образом оператора A и обозначают Im(A).
Теорема. Образ Im(A) линейного оператора A — линейное подпространство пространства Rn.
Теорема на лекции доказана.
Определение. Размерность образа линейного оператора называется рангом оператора, обозначается Rg(A): r=Rg(A)=dim Im(A).
Определение. Ядром
линейного оператора называется множество
элементов пространства Rn,
образом которых является нулевой
элемент. Ядро оператора обозначают
Ker(A): ![]() .
.
Теорема. Ядро линейного оператора — линейное подпространство пространства Rn.
Теорема на лекции доказана.
Определение. Размерность ядра линейного оператора называется дефектом оператора, обозначается def(A):r=def(A)=dimKer(A).
Для линейного
оператора![]() ,
действующего в пространстве Rn,
справедливы следующие утверждения:
,
действующего в пространстве Rn,
справедливы следующие утверждения:
1) ранг оператора равен рангу его матрицы;
2) ядро оператора совпадает с множеством решений линейной однородной системы с матрицей A, размерность пространства решений этой системы равна дефекту оператора, а ее фундаментальная система решений образует базис в ядре оператора;
столбцы, входящие в базисный минор матрицы оператора образуют базис в образе оператора.
Эти утверждения позволяют описать структуру образа и ядра линейного оператора (найти размерность подпространства и построить его базис), заданного матрицей, на языке матричных преобразований и общей теории линейных систем.
Примеры.
1. Ядро
и образ нулевого
оператора:
поскольку ![]() то
то ![]()
2. Ядро
и образ тождественного (единичного)
оператора:поскольку ![]() ,
то
,
то ![]()
3. Ядро
и образ оператора проектирования
пространства Rn на
подпространство Rn-1 параллельно
вектору ![]() :
поскольку
:
поскольку ![]() ,
то
,
то ![]()
4. Ядро
и образ оператора поворота пространства R3 против
часовой стрелки на угол относительно
оси вектора ![]() :
поскольку
:
поскольку ![]() ,
то
,
то ![]()
5.1.2 Матрица линейного оператора
Пусть
![]() , A —
линейный оператор в Rn.
, A —
линейный оператор в Rn.
Это
означает, что в некотором базисе ![]() в Rn имют
место разложения:
в Rn имют
место разложения:
![]() .
.
Поскольку A — линейный оператор, то
![]()
Но ![]() следовательно,
следовательно, ![]() т.е.
т.е. ![]() —
вектор из Rn,
компоненты которого — координаты образа
базисного вектора
—
вектор из Rn,
компоненты которого — координаты образа
базисного вектора ![]()
Продолжим вычисления:
![]()
Обозначим
 .
.
Тогда ![]() т.е.
т.е. ![]() .
.
Формула
связывает
вектор-столбец ![]() координат
образа с вектором-столбцом
координат
образа с вектором-столбцом ![]() координат
прообраза.
координат
прообраза.
Определение. Матрица, столбцами которой являются координаты образов соответствующих базисных векторов некоторого базиса в Rn —

называется матрицей линейного оператора A в данном базисе.
Обратите
внимание, теперь и в дальнейшем A (полужирная)
— обозначение линейного оператора, A(светлая)
или Ae —обозначение
матрицы оператора A в
некотором базисе или в базисе ![]() .
.
Таким образом, доказана следующая теорема.
Теорема (связь
координат образа и прообраза). Если в
пространстве Rn определен
некоторый базис,
и
—
векторы (столбцы) из Rn и ![]() ,
то векторы-столбцы их координат в этом
базисе связаны соотношением
,
где A — матрица оператора A в
этом же базисе.
,
то векторы-столбцы их координат в этом
базисе связаны соотношением
,
где A — матрица оператора A в
этом же базисе.
Между множеством линейных операторов, действующих в Rn и множеством квадратных матриц порядка n можно установить взаимно однозначное соответствие.
Примеры.
Матрица
нулевого оператора:
поскольку
то ![]() и,
следовательно матрица нулевого оператора
— нулевая матрица;
и,
следовательно матрица нулевого оператора
— нулевая матрица;
матрица
тождественного (единичного)
оператора:поскольку
,
то ![]() (единица
на i-м
месте), и, следовательно матрица
тождественного оператора — единичная
матрица;
(единица
на i-м
месте), и, следовательно матрица
тождественного оператора — единичная
матрица;
матрица
оператора проектирования пространства
Rn на
подпространство Rn-1 параллельно
вектору
:
поскольку
,
то ![]() и,
следовательно у матрицы A оператора
проектирования последний столбец
нулевой и она имеет вид:
и,
следовательно у матрицы A оператора
проектирования последний столбец
нулевой и она имеет вид:

матрица
оператора поворота пространства R3 против
часовой стрелки на угол ? относительно
оси вектора
:
поскольку
,
то ![]() и,
следовательно у матрицы A оператора
пооворота имеет вид:
и,
следовательно у матрицы A оператора
пооворота имеет вид:

5.1.3. Преобразование матрицы линейного оператора при изменении базиса
Как уже отмечалось, в пространстве Rn существует множество различных базисов.
Пусть
и ![]() — два базиса
в Rn.
— два базиса
в Rn.
Обозначим ![]() и
и ![]() координаты
векторов
и
из
Rn и
матрицу оператора A соответственно
в базисах
и
, а
координаты
векторов
и
из
Rn и
матрицу оператора A соответственно
в базисах
и
, а ![]() —
матрица перехода от базиса
к
базису
, т.е.
—
матрица перехода от базиса
к
базису
, т.е.
![]() ,
,
![]() ,
,
![]()
![]()
Тогда
![]()
откуда имеем
![]() —
формулы
преобразования матрицы линейного
оператора при изменении базиса.
—
формулы
преобразования матрицы линейного
оператора при изменении базиса.
5.1.4. Действия с линейными операторами
Для линейных операторов, как и для всех других новых объектов, с которыми мы познакомились в курсе линейной алгебры, можно определить линейные операции — операции сложения и умножения на число.
Определение. Суммой
операторов A и B называется
оператор, определенный в Rn на ![]() и
действующий следующим образом:
и
действующий следующим образом: ![]() .
.
Определение. Произведением
оператора A на
число ![]() называется
оператор, определенный в Rn на
называется
оператор, определенный в Rn на ![]() и
действующий следующим образом:
и
действующий следующим образом: ![]()
Определение. Произведением AB операторов A и B называется
оператор, определенный в Rn на ![]() и
действующий следующим образом:
и
действующий следующим образом: ![]()
На лекции доказано, что сумма линейных операторов, произведение линейного оператора на действительное число и произведение линейных операторов — линейный оператор.
Нетрудно доказать следующее утверждение: матрица суммы операторов в некоторм базисе равна сумме матриц слагаемых в том же базие, матрица оператора, являющегося произведением оператора на число — произведению матрицы оператора на число, а матрица произведения операторов — произведение матриц сомножителей.
