
- •Список основных статей по линейной алгебре
- •Аффинное пространство Точечно-векторная аксиоматика аффинного пространства
- •Для всех .
- •Базис и размерность векторного пространства Определение
- •Переход от одного базиса к другому
- •Билинейное отображение Определение
- •Билинейная форма
- •Матрица билинейной формы
- •Векторное пространство Определение
- •Подпространство векторного пространства
- •Для любых векторов ;
- •Для всех .
- •Факторпространство
- •Двойственное векторное пространство Определение
- •Для всех ;
- •Для всех .
- •Корневые подпространства
- •Квадратичная форма Определение
- •Квадратичная форма на векторном пространстве Определение
- •Матрица квадратичной формы
- •Квадратичная форма на вещественном векторном пространстве
- •Закон инерции квадратичных форм
- •Положительная определенность
- •Линейная зависимость
- •Линейные комбинации. Линейная оболочка
- •Линейная зависимость
- •Линейное нормированное пространство Определение
- •Линейное отображение векторных пространств Определение
- •Для всех ;
- •Для всех , .
- •Частные случаи
- •Свойства линейного отображения
- •Матрица Основные определения
- •Операции над матрицами Транспонирование
- •Сложение и умножение на скаляр
- •Умножение матриц
- •Матрица линейного отображения Определение
- •Определитель матрицы Определитель
- •Свойства определителя
- •Пересечение и сумма подпространств Пересечение и сумма
- •Внутренняя прямая сумма
- •Внешняя прямая сумма
- •Ранг матрицы Горизонтальный и вертикальный ранг
- •Элементарные преобразования матрицы
- •Минорный ранг
- •Свободный модуль Определение
- •Скалярное произведение Скалярное произведение
- •Евклидово пространство
- •Теорема Лапласа Минор
- •Алгебраическое дополнение
- •Теорема Лапласа
- •Определители 2-го порядка
- •Определители 3-го порядка
- •Определители высших порядков
- •Характеристический многочлен линейного оператора
- •Инвариантные подпространства
- •Собственные вектора и собственные значения
- •Характеристический многочлен
- •Диагонализируемые линейные операторы
- •Системы линейных уравнений Правило Крамера
- •7. 1 Линейные операторы и действия над ними
- •Базис и размерность пространства
Алгебраическое дополнение
Определение
3. Пусть
—
минор порядка
матрицы
,
построенный на строках с номерами
и
столбцах с номерами
.
Величину ![]() будем
называть алгебраическим
дополнением3) минора
.
будем
называть алгебраическим
дополнением3) минора
.
Пример
5. Алгебраическое
дополнение минора
из примера
4 равно ![]() .
Алгебраическое дополнение
элемента
из примера
3 равно
.
Алгебраическое дополнение
элемента
из примера
3 равно ![]() .
.
Теорема Лапласа
Теорема
1. (Теорема
Лапласа)
Зафиксируем в квадратной
матрице
произвольные
строк
с номерами
.
Тогда определитель матрицы
равен
сумме произведений всевозможных миноров,
построенных на этих строках, на их
алгебраическое дополнение. То есть ![]() .
.
Если
зафиксировать в матрице только одну
строку с номером
,
то, как частный случай из теоремы Лапласа,
получим следующую формулу:
![]() .
.
Пример
6. Вычислим
определитель матрицы
из примера
3 с
помощью разложения по первой строке:

 .
.
Определители 2-го порядка
Правило вычисления определителей 2-го порядка указано в примере 1.
Задача
1. Вычислить
определитель  .
.
Решение. 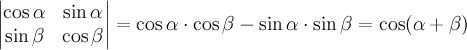 .
.
Определители 3-го порядка
Правило вычисления определителей 3-го порядка указано в примере 2.
Задача
2. Вычислить
определитель  .
.
Решение.
Способ
1. Вычислим
определитель по «правилу треугольника». 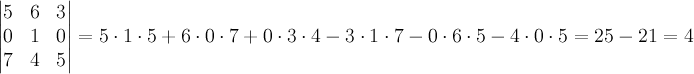 .
.
Способ
2. Используем теорему
Лапласа.
Разложим определитель по второй строке,
так как там только один ненулевой
элемент.  .
.
Способ
3. Разложим
определитель по первой строке:  .
Как видим, разложение по второй строке
было более целесообразно.
.
Как видим, разложение по второй строке
было более целесообразно.
Способ 4. Вычислим определитель с помощью элементарных преобразований, используя свойства определителя.
 (вычли
из третьей строки первую)
(вычли
из третьей строки первую)
 (вынесли
2 из третьей строки)
(вынесли
2 из третьей строки)
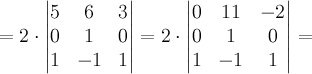 (вычли
из первой строки третью, умноженную на
5)
(вычли
из первой строки третью, умноженную на
5)
 (прибавили
к первой строки вторую, умноженную на
-11)
(прибавили
к первой строки вторую, умноженную на
-11)
 (поменяли
местами первую и третью строки; при этом
сменился знак)
(поменяли
местами первую и третью строки; при этом
сменился знак)
 .
(Для вычисления определителя
верхнетреугольной матрицы
применилипредложение
7.)
.
(Для вычисления определителя
верхнетреугольной матрицы
применилипредложение
7.)
Определители высших порядков
Задача 3. Вычислить определитель
 .
.
Решение. Применяя теорему Лапласа, разложим определитель по первым двум строкам. Перечислим все миноры порядка 2, построенные на 1-й и 2-й строках:
на 1-м и 2-м столбцах:
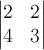 .
Его алгебраическое дополнение получается
вычеркиванием 1-й и 2-й строки и 1-го и
2-го столбца исходного определителя:
.
Его алгебраическое дополнение получается
вычеркиванием 1-й и 2-й строки и 1-го и
2-го столбца исходного определителя: 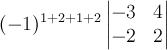 .
Число -1 возводится в степень, равную
сумме номеров строк и столбцов, на
которых построен минор: 1+2+1+2.
.
Число -1 возводится в степень, равную
сумме номеров строк и столбцов, на
которых построен минор: 1+2+1+2.на 1-м и 3-м столбцах:
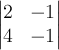 .
Его алгебраическое дополнение получается
вычеркиванием 1-й и 2-й строки и 1-го и
3-го столбца исходного определителя:
.
Его алгебраическое дополнение получается
вычеркиванием 1-й и 2-й строки и 1-го и
3-го столбца исходного определителя:  .
Число -1 возводится в степень, равную
сумме номеров строк и столбцов, на
которых построен минор: 1+2+1+3.
.
Число -1 возводится в степень, равную
сумме номеров строк и столбцов, на
которых построен минор: 1+2+1+3.на 1-м и 4-м столбцах:
 .
Его алгебраическое дополнение получается
вычеркиванием 1-й и 2-й строки и 1-го и
4-го столбца исходного определителя:
.
Его алгебраическое дополнение получается
вычеркиванием 1-й и 2-й строки и 1-го и
4-го столбца исходного определителя:  .
Число -1 возводится в степень, равную
сумме номеров строк и столбцов, на
которых построен минор: 1+2+1+4.
.
Число -1 возводится в степень, равную
сумме номеров строк и столбцов, на
которых построен минор: 1+2+1+4.на 2-м и 3-м столбцах:
 .
Его алгебраическое дополнение получается
вычеркиванием 1-й и 2-й строки и 2-го и
3-го столбца исходного определителя:
.
Его алгебраическое дополнение получается
вычеркиванием 1-й и 2-й строки и 2-го и
3-го столбца исходного определителя: 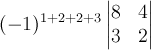 .
Число -1 возводится в степень, равную
сумме номеров строк и столбцов, на
которых построен минор: 1+2+2+3.
.
Число -1 возводится в степень, равную
сумме номеров строк и столбцов, на
которых построен минор: 1+2+2+3.на 2-м и 4-м столбцах:
 .
Его алгебраическое дополнение получается
вычеркиванием 1-й и 2-й строки и 2-го и
4-го столбца исходного определителя:
.
Число -1 возводится в степень, равную
сумме номеров строк и столбцов, на
которых построен минор: 1+2+2+4.
.
Его алгебраическое дополнение получается
вычеркиванием 1-й и 2-й строки и 2-го и
4-го столбца исходного определителя:
.
Число -1 возводится в степень, равную
сумме номеров строк и столбцов, на
которых построен минор: 1+2+2+4.на 3-м и 4-м столбцах:
 .
Его алгебраическое дополнение получается
вычеркиванием 1-й и 2-й строки и 3-го и
4-го столбца исходного определителя:
.
Его алгебраическое дополнение получается
вычеркиванием 1-й и 2-й строки и 3-го и
4-го столбца исходного определителя:  </latex>.
Число -1 возводится в степень, равную
сумме номеров строк и столбцов, на
которых построен минор: 1+2+3+4.
</latex>.
Число -1 возводится в степень, равную
сумме номеров строк и столбцов, на
которых построен минор: 1+2+3+4.
Согласно
теореме Лапласа, нужно умножить каждый
минор на его алгебраическое дополнение
и просуммировать результат: 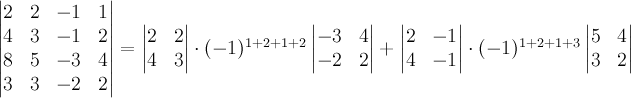

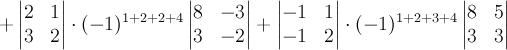
![]()
![]() .
.
Задача 4. Вычислить определитель
 .
.
Решение. С
помощью перестановки строк приведем
определитель к такому виду, чтобы
ненулевые элементы стояли на главной
диагонали.
Последовательно меняя соседние строки,
переместим первую строку вниз. При этом
будет выполнена ![]() перестановка.
Поэтому
перестановка.
Поэтому 
 (см.предложение
2).
(см.предложение
2).
Таким
же образом переместим верхнюю строчку
полученного определителя на
-е
место. При этом будет произведено ![]() операции,
и определитель примет вид
операции,
и определитель примет вид  .
.
Произведя
такую процедуру
раз,
получим определитель 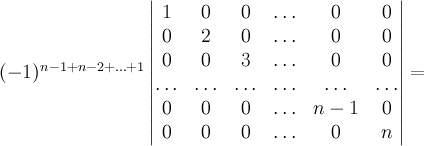

![]() .
(Для вычисления определителя
верхнетреугольной матрицы
применили предложение
7.)
.
(Для вычисления определителя
верхнетреугольной матрицы
применили предложение
7.)
Задача
5. Вычислить
определитель  .
.
Решение. Используя элементарные преобразования, приведем матрицу определителя к нижнетреугольному виду. А именно, вычтем из -й строки -ю. Затем из -й -ю, и т.д., наконец, вычтем из второй строки первую. В результате таких преобразований, согласно предложению 6, определитель не изменится, поэтому
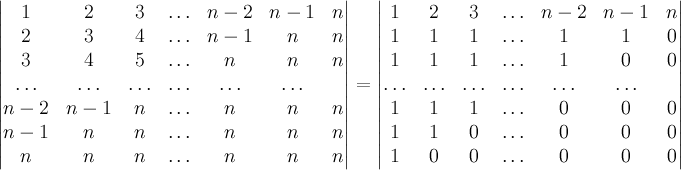 .
.
Теперь, как в предыдущей задаче поменяем строки местами так, чтобы матрица определителя стала нижнетреугольной.

![]() .
.
