
- •Список основных статей по линейной алгебре
- •Аффинное пространство Точечно-векторная аксиоматика аффинного пространства
- •Для всех .
- •Базис и размерность векторного пространства Определение
- •Переход от одного базиса к другому
- •Билинейное отображение Определение
- •Билинейная форма
- •Матрица билинейной формы
- •Векторное пространство Определение
- •Подпространство векторного пространства
- •Для любых векторов ;
- •Для всех .
- •Факторпространство
- •Двойственное векторное пространство Определение
- •Для всех ;
- •Для всех .
- •Корневые подпространства
- •Квадратичная форма Определение
- •Квадратичная форма на векторном пространстве Определение
- •Матрица квадратичной формы
- •Квадратичная форма на вещественном векторном пространстве
- •Закон инерции квадратичных форм
- •Положительная определенность
- •Линейная зависимость
- •Линейные комбинации. Линейная оболочка
- •Линейная зависимость
- •Линейное нормированное пространство Определение
- •Линейное отображение векторных пространств Определение
- •Для всех ;
- •Для всех , .
- •Частные случаи
- •Свойства линейного отображения
- •Матрица Основные определения
- •Операции над матрицами Транспонирование
- •Сложение и умножение на скаляр
- •Умножение матриц
- •Матрица линейного отображения Определение
- •Определитель матрицы Определитель
- •Свойства определителя
- •Пересечение и сумма подпространств Пересечение и сумма
- •Внутренняя прямая сумма
- •Внешняя прямая сумма
- •Ранг матрицы Горизонтальный и вертикальный ранг
- •Элементарные преобразования матрицы
- •Минорный ранг
- •Свободный модуль Определение
- •Скалярное произведение Скалярное произведение
- •Евклидово пространство
- •Теорема Лапласа Минор
- •Алгебраическое дополнение
- •Теорема Лапласа
- •Определители 2-го порядка
- •Определители 3-го порядка
- •Определители высших порядков
- •Характеристический многочлен линейного оператора
- •Инвариантные подпространства
- •Собственные вектора и собственные значения
- •Характеристический многочлен
- •Диагонализируемые линейные операторы
- •Системы линейных уравнений Правило Крамера
- •7. 1 Линейные операторы и действия над ними
- •Базис и размерность пространства
Список основных статей по линейной алгебре
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аффинное пространство Точечно-векторная аксиоматика аффинного пространства
Определение
1. ![]() -мерным
аффинным пространством над полем
-мерным
аффинным пространством над полем ![]() называется
множество точек и векторов, удовлетворяющих
следующим аксиомам:
называется
множество точек и векторов, удовлетворяющих
следующим аксиомам:
Существует по меньшей мере одна точка1).
Каждой паре точек
 ,
заданных в определенном порядке,
поставлен в соответствие один и только
один вектор,
который обозначается через
,
заданных в определенном порядке,
поставлен в соответствие один и только
один вектор,
который обозначается через  .
.Для каждой точки
 и
каждого вектора
и
каждого вектора  существует
одна и только одна точка
существует
одна и только одна точка  такая,
что
такая,
что 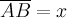 2).
2).(Аксиома параллелограмма.) Если
 ,
то
,
то  .
.Каждому вектору и каждому числу
 поставлен
в соответствие определенный вектор,
который обозначается
поставлен
в соответствие определенный вектор,
который обозначается  и
называется произведением вектора
на
число
и
называется произведением вектора
на
число  .
. для
любого вектора
.
для
любого вектора
.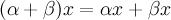 для
всех
для
всех  .
.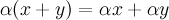 для
любых векторов
для
любых векторов  .
.Для всех .
Существует линейно независимых векторов, но любые
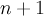 векторов
линейно зависимы между собой.
векторов
линейно зависимы между собой.
Пример
1. Трехмерное
пространство ![]() является
аффинным пространством, где точками
служат упорядоченные тройки чисел
является
аффинным пространством, где точками
служат упорядоченные тройки чисел ![]() .
.
Базис и размерность векторного пространства Определение
Определение
1. Базисом1) ненулевого векторного
пространства ![]() над полем
называется
система векторов,
которая
над полем
называется
система векторов,
которая
порождает ,
линейно независима.
Теорема 1. Ненулевое векторное пространство всегда обладает базисом. Иными словами, является свободным -модулем.
Определение
2. Размерностью2) ненулевого
векторного пространства ![]() называется мощность его
базиса. Для нулевого векторного
пространства
называется мощность его
базиса. Для нулевого векторного
пространства ![]() полагают,
что его размерность равна нулю. Размерность
векторного пространства
над
полем
обозначается
через
полагают,
что его размерность равна нулю. Размерность
векторного пространства
над
полем
обозначается
через ![]() .
.
Определение 3. Говорят, что пространство конечномерно3), если или базис состоит из конечного числа векторов. В противном случае говорят, что бесконечномерно4).
Пример
1. Поле действительных
чисел ![]() является
бесконечномерным векторным пространством
над полем рациональных
чисел
является
бесконечномерным векторным пространством
над полем рациональных
чисел ![]() .
.
Пример
2. Поле комплексных
чисел ![]() является
двумерным вещественным векторным
пространством5).
является
двумерным вещественным векторным
пространством5).
Пример
3. Произвольное
поле
является
одномерным векторным пространством
над собой с базисом ![]() .
.
Предложение
1. Для
конечномерного векторного пространства
набор векторов ![]() является
базисом, если каждый вектор
является
базисом, если каждый вектор ![]() единственным
образом представляется в виде
единственным
образом представляется в виде ![]() .
.
Определение
3. Пусть
—
базис
,
и ![]() .
Скаляры
.
Скаляры ![]() называютсякоординатами6) вектора
называютсякоординатами6) вектора ![]() в
данном базисе.
в
данном базисе.
Пример
4. Пусть
—
поле, и ![]() —
-мерное
координатное пространство.
Векторы
—
-мерное
координатное пространство.
Векторы ![]() составляют
базис
.
составляют
базис
.
Предложение 2. В конечномерном векторном пространстве число векторов базиса не зависит от выбора базиса.
